1.2.1 代入消元法 课件2
图片预览






文档简介
课件15张PPT。1.2.1代入消元法一:情景导入 妈妈在超市买苹果和梨,总共花了18元, 妈妈买的苹果比梨多1斤,苹果1斤3元,梨1斤2元,问妈妈买了多少斤苹果和梨?
解:设妈妈买了梨x斤梨,则苹果买了x+1斤;
2x+3(x+1)=18
x=3
所以,妈妈买了4斤苹果,3斤梨。
思考:可以列二元一次方程组解决这个问题吗? 解:设妈妈买了梨x斤,苹果y斤,则:
思考:
同学们观察所列的一元一次方程与二元一次方程组是同一问题的两种不同的解法,它们之间有怎样的关系?{y=x+1 ① 2x+3y=18 ②2x+3(x+1)=18二:探究知识 根据上面的解法解一元二次方程组
解:把①代入②,得
3×(y+3)-8y=14
-5y=5
y= -1
把y= -1代入①,得
x= -1+3=2
∴原方程组的解为{x=y+1 ① 3x-8y=14 ②{x= 2y= -1 思考:
(1)什么情况下把一个方程直接代入另一个方程?
(2)把y= -1可以代入②式吗?归纳:解二元一次方程组思想:
二元一次方程组中有两个未知数,如果消去其中的一个未知数,那么就把二元一次方程组转化为我们熟悉的一元一次方程,我们可以先求出一个未知数,然后再求另一个未知数,这种将未知数的个数由多到少,逐一解决的思想叫消元思想方法 .
把二元一次方程组中的一个未知数用含另个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫代入消元法,简称代入法变形:用代入法解方程组:
解:由①,得 x=1+y ③
把③代入②,得
3(1+y)-y=5
解得 y=1
把y=1代入③,得
x=2
∴原方程组的解为
{x-y=1 ① 3x-y=5 ②{x= 2y= 1 变形代入回代写解思考:此方程组中消去了哪个未知数,如果想消掉未知数x,该怎么变形?y=1可以代入①或②吗?求解例1 解二元一次方程组: 可以把求得的x,y的值代入原方程组检验,看是否为方程组的解.解由②式得y= -3x+1. ③把③代入①式,把x = -1代入③式,得y=4.解得 x = -1得 5x-(-3x+1)=-9.例2 用代入法解方程组:把y=2代入③ 式,得 x = 3把③代入 ②式 ,得解得 y = 2.
用代入法解方程组
分析(1)解这个方程组可以直接代入消元吗?
(2)通过怎样的变形实现消元?
解:由①,得 x= y ③
把③代入②,得
y-2y=5
解得 y=2
把y=2代入③,得
x=3
∴原方程组的解为{2x= 3y ①3x-2y= 5 ② {x= 2y= 3 知识提升用代入法解方程组
分析:
(1)可以直接用代入法求解吗?
(2)不能直接用代入法求解,那要通过怎样的变形实现消元?
(3)还有没有简便的方法呢?{2x-3y=1 ① 3x-6y= -1 ②解:由①,得 3y=2x-1 ③
把③代入②,得
3x-2×(2x-1)= -1
解得 x=3
把x=3代入③,得
3y=5
y=
∴原方程组的解为{x= 3y= 不用整体代入法该怎么做?整 体 代 入 法师生互动 小结1、解二元一次方程组的基本思想:
消元将二元一次方程组转化为一元一次方程
2、用代入法解二元一次方程组的步骤:
(1)将方程组里的一个方程变形,用一个未知数表示另一个未知数;(变形)
(2)将表示出来的未知数代入另一个方程化简,得到一个一元一次方程求解;(代入求解)
(3)把未知数的值返代方程中,求另一未知数 的值; ( 返代求另一未知数)
(4)写出方程组的解;(写解)变形技巧:变形的最终形式是:
将其中一个方程变为y=ax+b或x=ay+b,然后代入另一个方程实现消元②方程组中某一未知数的系数成倍数关系时可以 整体代入实现消元;③上述两种情况不具备时,就用等式的性质变形,用一个未知数表示另一个未知数;①方程组中有某一未知数的系数为1、-1时可直 接利用等式的性质变形;
解:设妈妈买了梨x斤梨,则苹果买了x+1斤;
2x+3(x+1)=18
x=3
所以,妈妈买了4斤苹果,3斤梨。
思考:可以列二元一次方程组解决这个问题吗? 解:设妈妈买了梨x斤,苹果y斤,则:
思考:
同学们观察所列的一元一次方程与二元一次方程组是同一问题的两种不同的解法,它们之间有怎样的关系?{y=x+1 ① 2x+3y=18 ②2x+3(x+1)=18二:探究知识 根据上面的解法解一元二次方程组
解:把①代入②,得
3×(y+3)-8y=14
-5y=5
y= -1
把y= -1代入①,得
x= -1+3=2
∴原方程组的解为{x=y+1 ① 3x-8y=14 ②{x= 2y= -1 思考:
(1)什么情况下把一个方程直接代入另一个方程?
(2)把y= -1可以代入②式吗?归纳:解二元一次方程组思想:
二元一次方程组中有两个未知数,如果消去其中的一个未知数,那么就把二元一次方程组转化为我们熟悉的一元一次方程,我们可以先求出一个未知数,然后再求另一个未知数,这种将未知数的个数由多到少,逐一解决的思想叫消元思想方法 .
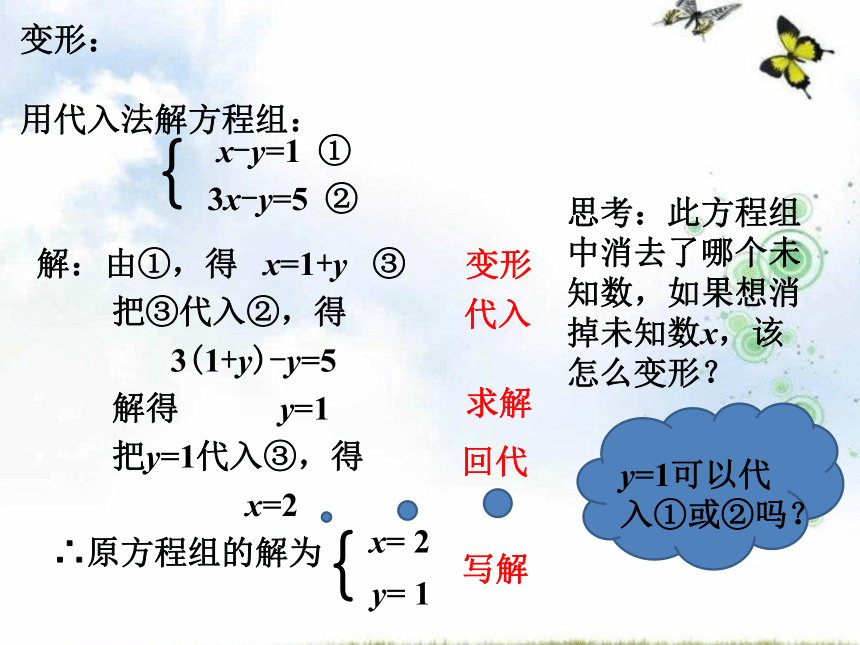
把二元一次方程组中的一个未知数用含另个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫代入消元法,简称代入法变形:用代入法解方程组:
解:由①,得 x=1+y ③
把③代入②,得
3(1+y)-y=5
解得 y=1
把y=1代入③,得
x=2
∴原方程组的解为
{x-y=1 ① 3x-y=5 ②{x= 2y= 1 变形代入回代写解思考:此方程组中消去了哪个未知数,如果想消掉未知数x,该怎么变形?y=1可以代入①或②吗?求解例1 解二元一次方程组: 可以把求得的x,y的值代入原方程组检验,看是否为方程组的解.解由②式得y= -3x+1. ③把③代入①式,把x = -1代入③式,得y=4.解得 x = -1得 5x-(-3x+1)=-9.例2 用代入法解方程组:把y=2代入③ 式,得 x = 3把③代入 ②式 ,得解得 y = 2.
用代入法解方程组
分析(1)解这个方程组可以直接代入消元吗?
(2)通过怎样的变形实现消元?
解:由①,得 x= y ③
把③代入②,得
y-2y=5
解得 y=2
把y=2代入③,得
x=3
∴原方程组的解为{2x= 3y ①3x-2y= 5 ② {x= 2y= 3 知识提升用代入法解方程组
分析:
(1)可以直接用代入法求解吗?
(2)不能直接用代入法求解,那要通过怎样的变形实现消元?
(3)还有没有简便的方法呢?{2x-3y=1 ① 3x-6y= -1 ②解:由①,得 3y=2x-1 ③
把③代入②,得
3x-2×(2x-1)= -1
解得 x=3
把x=3代入③,得
3y=5
y=
∴原方程组的解为{x= 3y= 不用整体代入法该怎么做?整 体 代 入 法师生互动 小结1、解二元一次方程组的基本思想:
消元将二元一次方程组转化为一元一次方程
2、用代入法解二元一次方程组的步骤:
(1)将方程组里的一个方程变形,用一个未知数表示另一个未知数;(变形)
(2)将表示出来的未知数代入另一个方程化简,得到一个一元一次方程求解;(代入求解)
(3)把未知数的值返代方程中,求另一未知数 的值; ( 返代求另一未知数)
(4)写出方程组的解;(写解)变形技巧:变形的最终形式是:
将其中一个方程变为y=ax+b或x=ay+b,然后代入另一个方程实现消元②方程组中某一未知数的系数成倍数关系时可以 整体代入实现消元;③上述两种情况不具备时,就用等式的性质变形,用一个未知数表示另一个未知数;①方程组中有某一未知数的系数为1、-1时可直 接利用等式的性质变形;
