湘教版八年级数学下册2.2.1平行四边形的性质测试卷(解析版)
文档属性
| 名称 | 湘教版八年级数学下册2.2.1平行四边形的性质测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 199.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-18 00:00:00 | ||
图片预览




文档简介
湘教版八年级数学下册
2.2.1
平行四边形的性质
测试卷
一.选择题(共10小题)
1.如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )
A.150°
B.130°
C.120°
D.100°
2.在 ABCD中,AB=3,BC=4,当 ABCD的面积最大时,下列结论正确的有( )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
A.①②③
B.①②④
C.②③④
D.①③④
3.如图, ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
A.13
B.17
C.20
D.26
4.如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3
5.关于 ABCD的叙述,正确的是( )
A.若AB⊥BC,则 ABCD是菱形
B.若AC⊥BD,则 ABCD是正方形
C.若AC=BD,则 ABCD是矩形
D.若AB=AD,则 ABCD是正方形
6.如图,在 ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
A.AG平分∠DAB
B.AD=DH
C.DH=BC
D.CH=DH
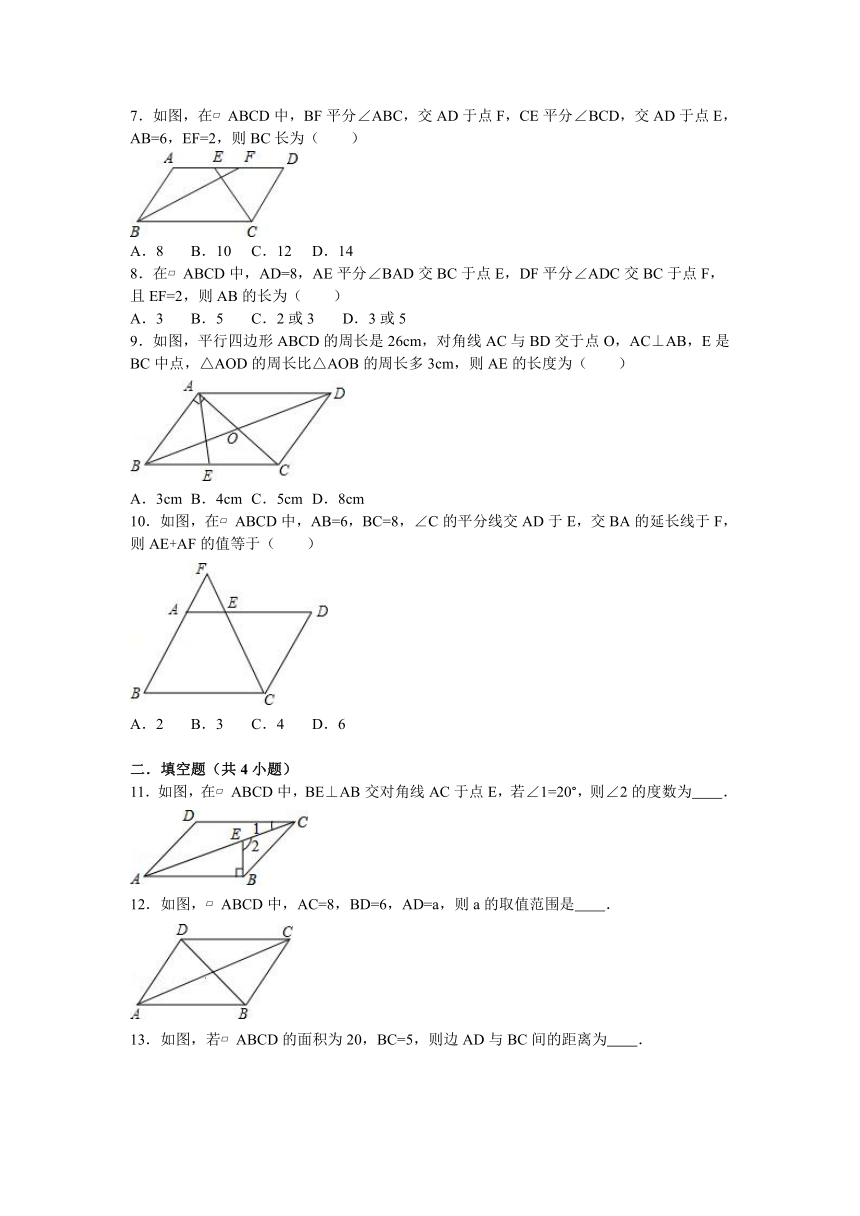
7.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
A.8
B.10
C.12
D.14
8.在 ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A.3
B.5
C.2或3
D.3或5
9.如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )
A.3cm
B.4cm
C.5cm
D.8cm
10.如图,在 ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A.2
B.3
C.4
D.6
二.填空题(共4小题)
11.如图,在 ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为 .
12.如图, ABCD中,AC=8,BD=6,AD=a,则a的取值范围是 .
13.如图,若 ABCD的面积为20,BC=5,则边AD与BC间的距离为 .
14.如图,在 ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是 .
三.解答题(共6小题)
15.如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
16.如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
17.如图,AC是 ABCD的对角线,∠BAC=∠DAC.
(1)求证:AB=BC;
(2)若AB=2,AC=2,求 ABCD的面积.
18.如图,在 ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
19.如图,E是 ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
20.已知:如图,在 ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什幺特殊四边形?请说明理由.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 河池)如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )
A.150°
B.130°
C.120°
D.100°
【分析】由在平行四边形ABCD中,∠ABC的平分线交AD于E,易证得△ABE是等腰三角形,又由∠BED=150°,即可求得∠A的大小.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABE,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∴AB=AE,
∵∠BED=150°,
∴∠ABE=∠AEB=30°,
∴∠A=180°﹣∠ABE﹣∠AEB=120°.
故选C.
【点评】此题考查了平行四边形的性质以及等腰三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.
2.(2016 菏泽)在 ABCD中,AB=3,BC=4,当 ABCD的面积最大时,下列结论正确的有( )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
A.①②③
B.①②④
C.②③④
D.①③④
【分析】当 ABCD的面积最大时,四边形ABCD为矩形,得出∠A=∠B=∠C=∠D=90°,AC=BD,根据勾股定理求出AC,即可得出结论.
【解答】解:根据题意得:当 ABCD的面积最大时,四边形ABCD为矩形,
∴∠A=∠B=∠C=∠D=90°,AC=BD,
∴AC==5,
①正确,②正确,④正确;③不正确;
故选:B.
【点评】本题考查了平行四边形的性质、矩形的性质以及勾股定理;得出 ABCD的面积最大时,四边形ABCD为矩形是解决问题的关键.
3.(2016 丽水)如图, ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
A.13
B.17
C.20
D.26
【分析】由平行四边形的性质得出OA=OC=3,OB=OD=6,BC=AD=8,即可求出△OBC的周长.
【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC=3,OB=OD=6,BC=AD=8,
∴△OBC的周长=OB+OC+AD=3+6+8=17.
故选:B.
【点评】本题主要考查了平行四边形的性质,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.
4.(2016 宁波)如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3
【分析】设等腰直角三角形的直角边为a,正方形边长为c,求出S2(用a、c表示),得出S1,S2,S3之间的关系,由此即可解决问题.
【解答】解:设等腰直角三角形的直角边为a,正方形边长为c,
则S2=(a+c)(a﹣c)=a2﹣c2,
∴S2=S1﹣S3,
∴S3=2S1﹣2S2,
∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1﹣2S2=4S1.
故选A.
【点评】本题考查平行四边形的性质、直角三角形的面积等知识,解题的关键是求出S1,S2,S3之间的关系,属于中考常考题型.
5.(2016 河北)关于 ABCD的叙述,正确的是( )
A.若AB⊥BC,则 ABCD是菱形
B.若AC⊥BD,则 ABCD是正方形
C.若AC=BD,则 ABCD是矩形
D.若AB=AD,则 ABCD是正方形
【分析】由菱形的判定方法、矩形的判定方法、正方形的判定方法得出选项A、B、D错误,C正确;即可得出结论.
【解答】解:∵ ABCD中,AB⊥BC,
∴四边形ABCD是矩形,不一定是菱形,选项A错误;
∵ ABCD中,AC⊥BD,
∴四边形ABCD是菱形,不一定是正方形,选项B错误;
∵ ABCD中,AC=BD,
∴四边形ABCD是矩形,选项C正确;
∵ ABCD中,AB=AD,
∴四边形ABCD是菱形,不一定是正方形,选项D错误;
故选:C.
【点评】本题考查了平行四边形的性质、菱形的判定方法、矩形的判定方法、正方形的判定方法;熟练掌握矩形、菱形、正方形的判定方法是解决问题的关键.
6.(2016 湖北襄阳)如图,在 ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
A.AG平分∠DAB
B.AD=DH
C.DH=BC
D.CH=DH
【分析】根据作图过程可得得AG平分∠DAB,再根据角平分线的性质和平行四边形的性质可证明∠DAH=∠DHA,进而得到AD=DH,
【解答】解:根据作图的方法可得AG平分∠DAB,
∵AG平分∠DAB,
∴∠DAH=∠BAH,
∵CD∥AB,
∴∠DHA=∠BAH,
∴∠DAH=∠DHA,
∴AD=DH,
∴BC=DH,
故选D.
【点评】此题主要考查了平行四边形的性质、角平分线的作法、平行线的性质;熟记平行四边形的性质是解决问题的关键关键.
7.(2016 丹东)如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
A.8
B.10
C.12
D.14
【分析】由平行四边形的性质和角平分线得出∠ABF=∠AFB,得出AF=AB=6,同理可证DE=DC=6,再由EF的长,即可求出BC的长.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,
∴∠AFB=∠FBC,
∵BF平分∠ABC,
∴∠ABF=∠FBC,
则∠ABF=∠AFB,
∴AF=AB=6,
同理可证:DE=DC=6,
∵EF=AF+DE﹣AD=2,
即6+6﹣AD=2,
解得:AD=10;
故选:B.
【点评】本题主要考查了平行四边形的性质、等腰三角形的判定;熟练掌握平行四边形的性质,证出AF=AB是解决问题的关键.
8.(2016 孝感)在 ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A.3
B.5
C.2或3
D.3或5
【分析】根据平行线的性质得到∠ADF=∠DFC,由DF平分∠ADC,得到∠ADF=∠CDF,等量代换得到∠DFC=∠FDC,根据等腰三角形的判定得到CF=CD,同理BE=AB,根据已知条件得到四边形ABCD是平行四边形,根据平行四边形的性质得到AB=CD,AD=BC,即可得到结论.
【解答】解:①如图1,在 ABCD中,∵BC=AD=8,BC∥AD,CD=AB,CD∥AB,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∵AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,
∴∠BAE=∠DAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CFD=∠CDF,
∴AB=BE,CF=CD,
∵EF=2,
∴BC=BE+CF﹣EF=2AB﹣EF=8,
∴AB=5;
②在 ABCD中,∵BC=AD=8,BC∥AD,CD=AB,CD∥AB,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∵AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,
∴∠BAE=∠DAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CFD=∠CDF,
∴AB=BE,CF=CD,
∵EF=2,
∴BC=BE+CF=2AB+EF=8,
∴AB=3;
综上所述:AB的长为3或5.
故选D.
【点评】本题考查了等腰三角形的判定和性质,平行线的性质,平行四边形的性质,解答本题的关键是判断出BA=BE=CF=CD.
9.(2016 绵阳)如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )
A.3cm
B.4cm
C.5cm
D.8cm
【分析】由 ABCD的周长为26cm,对角线AC、BD相交于点0,若△AOD的周长比△AOB的周长多3cm,可得AB+AD=13cm,AD﹣AB=3cm,求出AB和AD的长,得出BC的长,再由直角三角形斜边上的中线性质即可求得答案.
【解答】解:∵ ABCD的周长为26cm,
∴AB+AD=13cm,OB=OD,
∵△AOD的周长比△AOB的周长多3cm,
∴(OA+OB+AD)﹣(OA+OD+AB)=AD﹣AB=3cm,
∴AB=5cm,AD=8cm.
∴BC=AD=8cm.
∵AC⊥AB,E是BC中点,
∴AE=BC=4cm;
故选:B.
【点评】此题考查了平行四边形的性质、直角三角形斜边上的中线性质.熟练掌握平行四边形的性质,由直角三角形斜边上的中线性质求出AE是解决问题的关键.
10.(2016 泰安)如图,在 ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A.2
B.3
C.4
D.6
【分析】由平行四边形的性质和角平分线得出∠F=∠FCB,证出BF=BC=8,同理:DE=CD=6,求出AF=BF﹣AB=2,AE=AD﹣DE=2,即可得出结果.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC=8,CD=AB=6,
∴∠F=∠DCF,
∵∠C平分线为CF,
∴∠FCB=∠DCF,
∴∠F=∠FCB,
∴BF=BC=8,
同理:DE=CD=6,
∴AF=BF﹣AB=2,AE=AD﹣DE=2,
∴AE+AF=4;
故选:C.
【点评】本题考查了平行四边形的性质、等腰三角形的判定;熟练掌握平行四边形的性质,证明三角形是等腰三角形是解决问题的关键.
二.填空题(共4小题)
11.(2016 河南)如图,在 ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为 110° .
【分析】首先由在 ABCD中,∠1=20°,求得∠BAE的度数,然后由BE⊥AB,利用三角形外角的性质,求得∠2的度数.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAE=∠1=20°,
∵BE⊥AB,
∴∠ABE=90°,
∴∠2=∠BAE+∠ABE=110°.
故答案为:110°.
【点评】此题考查了平行四边形的性质以及三角形外角的性质.注意平行四边形的对边互相平行.
12.(2016 巴中)如图, ABCD中,AC=8,BD=6,AD=a,则a的取值范围是 1<a<7 .
【分析】由平行四边形的性质得出OA=4,OD=3,再由三角形的三边关系即可得出结果.
【解答】解:如图所示:
∵四边形ABCD是平行四边形,
∴OA=AC=4,OD=BD=3,
在△AOD中,由三角形的三边关系得:4﹣3<AD<4+3.
即1<a<7;
故答案为:1<a<7.
【点评】本题考查了平行四边形的性质和三角形的三边关系;熟练掌握平行四边形的性质,由三角形的三边关系得出结果是解决问题的关键.
13.(2016 柳州)如图,若 ABCD的面积为20,BC=5,则边AD与BC间的距离为 4 .
【分析】过A作AH⊥BC,根据平行四边形的面积公式可得5AH=20,解出AH的长,进而可得答案.
【解答】解:过A作AH⊥BC,
∵ ABCD的面积为20,BC=5,
∴5AH=20,
AH=4,
∴边AD与BC间的距离为4,
故答案为:4.
【点评】此题主要考查了平行四边形的性质,关键是掌握平行四边形的面积公式:底×高.
14.(2016 新疆)如图,在 ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是 24 .
【分析】根据平行四边形性质得出AD∥CB,AB∥CD,推出∠DAB+∠CBA=180°,求出∠PAB+∠PBA=90°,在△APB中求出∠APB=90°,由勾股定理求出BP,证出AD=DP=5,BC=PC=5,得出DC=10=AB,即可求出答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°﹣(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在Rt△APB中,AB=10,AP=8,
∴BP==6,
∴△APB的周长=6+8+10=24;
故答案为:24.
【点评】本题考查了平行四边形性质,平行线性质,等腰三角形的性质和判定,三角形的内角和定理,勾股定理等知识点的综合运用.
三.解答题(共6小题)
15.(2016 梅州)如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
【分析】(1)由平行四边形的性质和AAS证明△OBE≌△ODF,得出对应边相等即可;
(2)证出AE=GE,再证明DG=DO,得出OF=FG=1,即可得出结果.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠OBE=∠ODF.
在△OBE与△ODF中,
∴△OBE≌△ODF(AAS).
∴BO=DO.
(2)解:∵EF⊥AB,AB∥DC,
∴∠GEA=∠GFD=90°.
∵∠A=45°,
∴∠G=∠A=45°.
∴AE=GE
∵BD⊥AD,
∴∠ADB=∠GDO=90°.
∴∠GOD=∠G=45°.
∴DG=DO,
∴OF=FG=1,
由(1)可知,OE=OF=1,
∴GE=OE+OF+FG=3,
∴AE=3.
【点评】本题考查了平行四边形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题(1)的关键.
16.(2016 永州)如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
【分析】(1)由平行四边形的性质和角平分线得出∠BAE=∠BEA,即可得出AB=BE;
(2)先证明△ABE是等边三角形,得出AE=AB=4,AF=EF=2,由勾股定理求出BF,由AAS证明△ADF≌△ECF,得出△ADF的面积=△ECF的面积,因此平行四边形ABCD的面积=△ABE的面积=AE BF,即可得出结果.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠B+∠C=180°,∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,∴BE=CD;
(2)解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,
∴AE=AB=4,
∵BF⊥AE,
∴AF=EF=2,
∴BF===2,
∵AD∥BC,
∴∠D=∠ECF,∠DAF=∠E,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(AAS),
∴△ADF的面积=△ECF的面积,
∴平行四边形ABCD的面积=△ABE的面积=AE BF=×4×2=4.
【点评】此题考查了平行四边形的性质、全等三角形的判定与性质、等腰三角形的判定、等边三角形的判定与性质、勾股定理;熟练掌握平行四边形的性质,证明三角形全等是解决问题(2)的关键.
17.(2016 长沙)如图,AC是 ABCD的对角线,∠BAC=∠DAC.
(1)求证:AB=BC;
(2)若AB=2,AC=2,求 ABCD的面积.
【分析】(1)由平行四边形的性质得出∠DAC=∠BCA,再由已知条件得出∠BAC=∠BCA,即可得出AB=BC;
(2)连接BD交AC于O,证明四边形ABCD是菱形,得出AC⊥BD,OA=OC=AC=,OB=OD=BD,由勾股定理求出OB,得出BD, ABCD的面积=AC BD,即可得出结果.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠BCA,
∵∠BAC=∠DAC,
∴∠BAC=∠BCA,
∴AB=BC;
(2)解:连接BD交AC于O,如图所示:
∵四边形ABCD是平行四边形,AB=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=,OB=OD=BD,
∴OB===1,
∴BD=2OB=2,
∴ ABCD的面积=AC BD=×2×2=2.
【点评】本题考查了平行四边形的性质、等腰三角形的判定、勾股定理、菱形面积的计算;熟练掌握平行四边形的性质,证明四边形是菱形是解决问题的关键.
18.(2016 西宁)如图,在 ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
【分析】(1)由在 ABCD中,E是BC的中点,利用ASA,即可判定△ABE≌△FCE,继而证得结论;
(2)由AD=2AB,AB=FC=CD,可得AD=DF,又由△ABE≌△FCE,可得AE=EF,然后利用三线合一,证得结论.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠ABE=∠FCE,
∵E为BC中点,
∴BE=CE,
在△ABE与△FCE中,
,
∴△ABE≌△FCE(ASA),
∴AB=FC;
(2)∵AD=2AB,AB=FC=CD,
∴AD=DF,
∵△ABE≌△FCE,
∴AE=EF,
∴DE⊥AF.
【点评】此题考查了平行四边形的性质、全等三角形的判定与性质以及等腰三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.
19.(2016 温州)如图,E是 ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
【分析】(1)由平行四边形的性质得出AD∥BC,AB∥CD,证出∠DAE=∠F,∠D=∠ECF,由AAS证明△ADE≌△FCE即可;
(2)由全等三角形的性质得出AE=EF=3,由平行线的性质证出∠AED=∠BAF=90°,由勾股定理求出DE,即可得出CD的长.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAE=∠F,∠D=∠ECF,
∵E是 ABCD的边CD的中点,
∴DE=CE,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS);
(2)解:∵ADE≌△FCE,
∴AE=EF=3,
∵AB∥CD,
∴∠AED=∠BAF=90°,
在 ABCD中,AD=BC=5,
∴DE===4,
∴CD=2DE=8.
【点评】此题考查了平行四边形的性质、全等三角形的判定方法、勾股定理;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.
20.(2016 青岛)已知:如图,在 ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什幺特殊四边形?请说明理由.
【分析】(1)由平行四边形的性质得出AB=CD,∠BAE=∠DCF,由SAS证明△ABE≌△CDF即可;
(2)由平行四边形的性质得出AD∥BC,AD=BC,证出DE=BF,得出四边形BEDF是平行四边形,得出OB=OD,再由等腰三角形的三线合一性质得出EF⊥BD,即可得出四边形BEDF是菱形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAE=∠DCF,
在△ABE和△CDF中,,
∴△ABE≌△CDF(SAS);
(2)解:四边形BEDF是菱形;理由如下:如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BEDF是平行四边形,
∴OB=OD,
∵DG=BG,
∴EF⊥BD,
∴四边形BEDF是菱形.
【点评】此题考查了平行四边形的性质、全等三角形的判定与性质、菱形的判定.熟练掌握平行四边形的性质,证出四边形BEDF是平行四边形是解决问题(2)的关键.
2.2.1
平行四边形的性质
测试卷
一.选择题(共10小题)
1.如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )
A.150°
B.130°
C.120°
D.100°
2.在 ABCD中,AB=3,BC=4,当 ABCD的面积最大时,下列结论正确的有( )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
A.①②③
B.①②④
C.②③④
D.①③④
3.如图, ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
A.13
B.17
C.20
D.26
4.如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3
5.关于 ABCD的叙述,正确的是( )
A.若AB⊥BC,则 ABCD是菱形
B.若AC⊥BD,则 ABCD是正方形
C.若AC=BD,则 ABCD是矩形
D.若AB=AD,则 ABCD是正方形
6.如图,在 ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
A.AG平分∠DAB
B.AD=DH
C.DH=BC
D.CH=DH
7.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
A.8
B.10
C.12
D.14
8.在 ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A.3
B.5
C.2或3
D.3或5
9.如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )
A.3cm
B.4cm
C.5cm
D.8cm
10.如图,在 ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A.2
B.3
C.4
D.6
二.填空题(共4小题)
11.如图,在 ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为 .
12.如图, ABCD中,AC=8,BD=6,AD=a,则a的取值范围是 .
13.如图,若 ABCD的面积为20,BC=5,则边AD与BC间的距离为 .
14.如图,在 ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是 .
三.解答题(共6小题)
15.如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
16.如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
17.如图,AC是 ABCD的对角线,∠BAC=∠DAC.
(1)求证:AB=BC;
(2)若AB=2,AC=2,求 ABCD的面积.
18.如图,在 ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
19.如图,E是 ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
20.已知:如图,在 ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什幺特殊四边形?请说明理由.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 河池)如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )
A.150°
B.130°
C.120°
D.100°
【分析】由在平行四边形ABCD中,∠ABC的平分线交AD于E,易证得△ABE是等腰三角形,又由∠BED=150°,即可求得∠A的大小.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABE,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∴AB=AE,
∵∠BED=150°,
∴∠ABE=∠AEB=30°,
∴∠A=180°﹣∠ABE﹣∠AEB=120°.
故选C.
【点评】此题考查了平行四边形的性质以及等腰三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.
2.(2016 菏泽)在 ABCD中,AB=3,BC=4,当 ABCD的面积最大时,下列结论正确的有( )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
A.①②③
B.①②④
C.②③④
D.①③④
【分析】当 ABCD的面积最大时,四边形ABCD为矩形,得出∠A=∠B=∠C=∠D=90°,AC=BD,根据勾股定理求出AC,即可得出结论.
【解答】解:根据题意得:当 ABCD的面积最大时,四边形ABCD为矩形,
∴∠A=∠B=∠C=∠D=90°,AC=BD,
∴AC==5,
①正确,②正确,④正确;③不正确;
故选:B.
【点评】本题考查了平行四边形的性质、矩形的性质以及勾股定理;得出 ABCD的面积最大时,四边形ABCD为矩形是解决问题的关键.
3.(2016 丽水)如图, ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
A.13
B.17
C.20
D.26
【分析】由平行四边形的性质得出OA=OC=3,OB=OD=6,BC=AD=8,即可求出△OBC的周长.
【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC=3,OB=OD=6,BC=AD=8,
∴△OBC的周长=OB+OC+AD=3+6+8=17.
故选:B.
【点评】本题主要考查了平行四边形的性质,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.
4.(2016 宁波)如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3
【分析】设等腰直角三角形的直角边为a,正方形边长为c,求出S2(用a、c表示),得出S1,S2,S3之间的关系,由此即可解决问题.
【解答】解:设等腰直角三角形的直角边为a,正方形边长为c,
则S2=(a+c)(a﹣c)=a2﹣c2,
∴S2=S1﹣S3,
∴S3=2S1﹣2S2,
∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1﹣2S2=4S1.
故选A.
【点评】本题考查平行四边形的性质、直角三角形的面积等知识,解题的关键是求出S1,S2,S3之间的关系,属于中考常考题型.
5.(2016 河北)关于 ABCD的叙述,正确的是( )
A.若AB⊥BC,则 ABCD是菱形
B.若AC⊥BD,则 ABCD是正方形
C.若AC=BD,则 ABCD是矩形
D.若AB=AD,则 ABCD是正方形
【分析】由菱形的判定方法、矩形的判定方法、正方形的判定方法得出选项A、B、D错误,C正确;即可得出结论.
【解答】解:∵ ABCD中,AB⊥BC,
∴四边形ABCD是矩形,不一定是菱形,选项A错误;
∵ ABCD中,AC⊥BD,
∴四边形ABCD是菱形,不一定是正方形,选项B错误;
∵ ABCD中,AC=BD,
∴四边形ABCD是矩形,选项C正确;
∵ ABCD中,AB=AD,
∴四边形ABCD是菱形,不一定是正方形,选项D错误;
故选:C.
【点评】本题考查了平行四边形的性质、菱形的判定方法、矩形的判定方法、正方形的判定方法;熟练掌握矩形、菱形、正方形的判定方法是解决问题的关键.
6.(2016 湖北襄阳)如图,在 ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
A.AG平分∠DAB
B.AD=DH
C.DH=BC
D.CH=DH
【分析】根据作图过程可得得AG平分∠DAB,再根据角平分线的性质和平行四边形的性质可证明∠DAH=∠DHA,进而得到AD=DH,
【解答】解:根据作图的方法可得AG平分∠DAB,
∵AG平分∠DAB,
∴∠DAH=∠BAH,
∵CD∥AB,
∴∠DHA=∠BAH,
∴∠DAH=∠DHA,
∴AD=DH,
∴BC=DH,
故选D.
【点评】此题主要考查了平行四边形的性质、角平分线的作法、平行线的性质;熟记平行四边形的性质是解决问题的关键关键.
7.(2016 丹东)如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
A.8
B.10
C.12
D.14
【分析】由平行四边形的性质和角平分线得出∠ABF=∠AFB,得出AF=AB=6,同理可证DE=DC=6,再由EF的长,即可求出BC的长.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,
∴∠AFB=∠FBC,
∵BF平分∠ABC,
∴∠ABF=∠FBC,
则∠ABF=∠AFB,
∴AF=AB=6,
同理可证:DE=DC=6,
∵EF=AF+DE﹣AD=2,
即6+6﹣AD=2,
解得:AD=10;
故选:B.
【点评】本题主要考查了平行四边形的性质、等腰三角形的判定;熟练掌握平行四边形的性质,证出AF=AB是解决问题的关键.
8.(2016 孝感)在 ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A.3
B.5
C.2或3
D.3或5
【分析】根据平行线的性质得到∠ADF=∠DFC,由DF平分∠ADC,得到∠ADF=∠CDF,等量代换得到∠DFC=∠FDC,根据等腰三角形的判定得到CF=CD,同理BE=AB,根据已知条件得到四边形ABCD是平行四边形,根据平行四边形的性质得到AB=CD,AD=BC,即可得到结论.
【解答】解:①如图1,在 ABCD中,∵BC=AD=8,BC∥AD,CD=AB,CD∥AB,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∵AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,
∴∠BAE=∠DAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CFD=∠CDF,
∴AB=BE,CF=CD,
∵EF=2,
∴BC=BE+CF﹣EF=2AB﹣EF=8,
∴AB=5;
②在 ABCD中,∵BC=AD=8,BC∥AD,CD=AB,CD∥AB,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∵AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,
∴∠BAE=∠DAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CFD=∠CDF,
∴AB=BE,CF=CD,
∵EF=2,
∴BC=BE+CF=2AB+EF=8,
∴AB=3;
综上所述:AB的长为3或5.
故选D.
【点评】本题考查了等腰三角形的判定和性质,平行线的性质,平行四边形的性质,解答本题的关键是判断出BA=BE=CF=CD.
9.(2016 绵阳)如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )
A.3cm
B.4cm
C.5cm
D.8cm
【分析】由 ABCD的周长为26cm,对角线AC、BD相交于点0,若△AOD的周长比△AOB的周长多3cm,可得AB+AD=13cm,AD﹣AB=3cm,求出AB和AD的长,得出BC的长,再由直角三角形斜边上的中线性质即可求得答案.
【解答】解:∵ ABCD的周长为26cm,
∴AB+AD=13cm,OB=OD,
∵△AOD的周长比△AOB的周长多3cm,
∴(OA+OB+AD)﹣(OA+OD+AB)=AD﹣AB=3cm,
∴AB=5cm,AD=8cm.
∴BC=AD=8cm.
∵AC⊥AB,E是BC中点,
∴AE=BC=4cm;
故选:B.
【点评】此题考查了平行四边形的性质、直角三角形斜边上的中线性质.熟练掌握平行四边形的性质,由直角三角形斜边上的中线性质求出AE是解决问题的关键.
10.(2016 泰安)如图,在 ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A.2
B.3
C.4
D.6
【分析】由平行四边形的性质和角平分线得出∠F=∠FCB,证出BF=BC=8,同理:DE=CD=6,求出AF=BF﹣AB=2,AE=AD﹣DE=2,即可得出结果.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC=8,CD=AB=6,
∴∠F=∠DCF,
∵∠C平分线为CF,
∴∠FCB=∠DCF,
∴∠F=∠FCB,
∴BF=BC=8,
同理:DE=CD=6,
∴AF=BF﹣AB=2,AE=AD﹣DE=2,
∴AE+AF=4;
故选:C.
【点评】本题考查了平行四边形的性质、等腰三角形的判定;熟练掌握平行四边形的性质,证明三角形是等腰三角形是解决问题的关键.
二.填空题(共4小题)
11.(2016 河南)如图,在 ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为 110° .
【分析】首先由在 ABCD中,∠1=20°,求得∠BAE的度数,然后由BE⊥AB,利用三角形外角的性质,求得∠2的度数.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAE=∠1=20°,
∵BE⊥AB,
∴∠ABE=90°,
∴∠2=∠BAE+∠ABE=110°.
故答案为:110°.
【点评】此题考查了平行四边形的性质以及三角形外角的性质.注意平行四边形的对边互相平行.
12.(2016 巴中)如图, ABCD中,AC=8,BD=6,AD=a,则a的取值范围是 1<a<7 .
【分析】由平行四边形的性质得出OA=4,OD=3,再由三角形的三边关系即可得出结果.
【解答】解:如图所示:
∵四边形ABCD是平行四边形,
∴OA=AC=4,OD=BD=3,
在△AOD中,由三角形的三边关系得:4﹣3<AD<4+3.
即1<a<7;
故答案为:1<a<7.
【点评】本题考查了平行四边形的性质和三角形的三边关系;熟练掌握平行四边形的性质,由三角形的三边关系得出结果是解决问题的关键.
13.(2016 柳州)如图,若 ABCD的面积为20,BC=5,则边AD与BC间的距离为 4 .
【分析】过A作AH⊥BC,根据平行四边形的面积公式可得5AH=20,解出AH的长,进而可得答案.
【解答】解:过A作AH⊥BC,
∵ ABCD的面积为20,BC=5,
∴5AH=20,
AH=4,
∴边AD与BC间的距离为4,
故答案为:4.
【点评】此题主要考查了平行四边形的性质,关键是掌握平行四边形的面积公式:底×高.
14.(2016 新疆)如图,在 ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是 24 .
【分析】根据平行四边形性质得出AD∥CB,AB∥CD,推出∠DAB+∠CBA=180°,求出∠PAB+∠PBA=90°,在△APB中求出∠APB=90°,由勾股定理求出BP,证出AD=DP=5,BC=PC=5,得出DC=10=AB,即可求出答案.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°﹣(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在Rt△APB中,AB=10,AP=8,
∴BP==6,
∴△APB的周长=6+8+10=24;
故答案为:24.
【点评】本题考查了平行四边形性质,平行线性质,等腰三角形的性质和判定,三角形的内角和定理,勾股定理等知识点的综合运用.
三.解答题(共6小题)
15.(2016 梅州)如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
【分析】(1)由平行四边形的性质和AAS证明△OBE≌△ODF,得出对应边相等即可;
(2)证出AE=GE,再证明DG=DO,得出OF=FG=1,即可得出结果.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠OBE=∠ODF.
在△OBE与△ODF中,
∴△OBE≌△ODF(AAS).
∴BO=DO.
(2)解:∵EF⊥AB,AB∥DC,
∴∠GEA=∠GFD=90°.
∵∠A=45°,
∴∠G=∠A=45°.
∴AE=GE
∵BD⊥AD,
∴∠ADB=∠GDO=90°.
∴∠GOD=∠G=45°.
∴DG=DO,
∴OF=FG=1,
由(1)可知,OE=OF=1,
∴GE=OE+OF+FG=3,
∴AE=3.
【点评】本题考查了平行四边形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题(1)的关键.
16.(2016 永州)如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
【分析】(1)由平行四边形的性质和角平分线得出∠BAE=∠BEA,即可得出AB=BE;
(2)先证明△ABE是等边三角形,得出AE=AB=4,AF=EF=2,由勾股定理求出BF,由AAS证明△ADF≌△ECF,得出△ADF的面积=△ECF的面积,因此平行四边形ABCD的面积=△ABE的面积=AE BF,即可得出结果.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠B+∠C=180°,∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,∴BE=CD;
(2)解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,
∴AE=AB=4,
∵BF⊥AE,
∴AF=EF=2,
∴BF===2,
∵AD∥BC,
∴∠D=∠ECF,∠DAF=∠E,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(AAS),
∴△ADF的面积=△ECF的面积,
∴平行四边形ABCD的面积=△ABE的面积=AE BF=×4×2=4.
【点评】此题考查了平行四边形的性质、全等三角形的判定与性质、等腰三角形的判定、等边三角形的判定与性质、勾股定理;熟练掌握平行四边形的性质,证明三角形全等是解决问题(2)的关键.
17.(2016 长沙)如图,AC是 ABCD的对角线,∠BAC=∠DAC.
(1)求证:AB=BC;
(2)若AB=2,AC=2,求 ABCD的面积.
【分析】(1)由平行四边形的性质得出∠DAC=∠BCA,再由已知条件得出∠BAC=∠BCA,即可得出AB=BC;
(2)连接BD交AC于O,证明四边形ABCD是菱形,得出AC⊥BD,OA=OC=AC=,OB=OD=BD,由勾股定理求出OB,得出BD, ABCD的面积=AC BD,即可得出结果.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠BCA,
∵∠BAC=∠DAC,
∴∠BAC=∠BCA,
∴AB=BC;
(2)解:连接BD交AC于O,如图所示:
∵四边形ABCD是平行四边形,AB=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=,OB=OD=BD,
∴OB===1,
∴BD=2OB=2,
∴ ABCD的面积=AC BD=×2×2=2.
【点评】本题考查了平行四边形的性质、等腰三角形的判定、勾股定理、菱形面积的计算;熟练掌握平行四边形的性质,证明四边形是菱形是解决问题的关键.
18.(2016 西宁)如图,在 ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
【分析】(1)由在 ABCD中,E是BC的中点,利用ASA,即可判定△ABE≌△FCE,继而证得结论;
(2)由AD=2AB,AB=FC=CD,可得AD=DF,又由△ABE≌△FCE,可得AE=EF,然后利用三线合一,证得结论.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠ABE=∠FCE,
∵E为BC中点,
∴BE=CE,
在△ABE与△FCE中,
,
∴△ABE≌△FCE(ASA),
∴AB=FC;
(2)∵AD=2AB,AB=FC=CD,
∴AD=DF,
∵△ABE≌△FCE,
∴AE=EF,
∴DE⊥AF.
【点评】此题考查了平行四边形的性质、全等三角形的判定与性质以及等腰三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.
19.(2016 温州)如图,E是 ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
【分析】(1)由平行四边形的性质得出AD∥BC,AB∥CD,证出∠DAE=∠F,∠D=∠ECF,由AAS证明△ADE≌△FCE即可;
(2)由全等三角形的性质得出AE=EF=3,由平行线的性质证出∠AED=∠BAF=90°,由勾股定理求出DE,即可得出CD的长.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAE=∠F,∠D=∠ECF,
∵E是 ABCD的边CD的中点,
∴DE=CE,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS);
(2)解:∵ADE≌△FCE,
∴AE=EF=3,
∵AB∥CD,
∴∠AED=∠BAF=90°,
在 ABCD中,AD=BC=5,
∴DE===4,
∴CD=2DE=8.
【点评】此题考查了平行四边形的性质、全等三角形的判定方法、勾股定理;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.
20.(2016 青岛)已知:如图,在 ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什幺特殊四边形?请说明理由.
【分析】(1)由平行四边形的性质得出AB=CD,∠BAE=∠DCF,由SAS证明△ABE≌△CDF即可;
(2)由平行四边形的性质得出AD∥BC,AD=BC,证出DE=BF,得出四边形BEDF是平行四边形,得出OB=OD,再由等腰三角形的三线合一性质得出EF⊥BD,即可得出四边形BEDF是菱形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAE=∠DCF,
在△ABE和△CDF中,,
∴△ABE≌△CDF(SAS);
(2)解:四边形BEDF是菱形;理由如下:如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BEDF是平行四边形,
∴OB=OD,
∵DG=BG,
∴EF⊥BD,
∴四边形BEDF是菱形.
【点评】此题考查了平行四边形的性质、全等三角形的判定与性质、菱形的判定.熟练掌握平行四边形的性质,证出四边形BEDF是平行四边形是解决问题(2)的关键.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
