湘教版九年级数学下册3.2直棱柱、圆锥的侧面展开图测试卷(解析版)
文档属性
| 名称 | 湘教版九年级数学下册3.2直棱柱、圆锥的侧面展开图测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 187.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-18 00:00:00 | ||
图片预览




文档简介
湘教版九年级数学下册3.2直棱柱、圆锥的侧面展开图测试卷
一.选择题(共10小题)
1.如图是一个正方体,则它的表面展开图可以是( )
A.
B.
C.
D.
2.如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
A.
B.
C.
D.
3.下列图形中,不可以作为一个正方体的展开图的是( )
A.
B.
C.
D.
4.将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A.
B.
C.
D.
5.如图1所示,将一个正四棱锥(底面为正方形,四条测棱相等)的其中四条边剪开,得到图2,则被剪开的四条边有可能是( )
A.PA,PB,AD,BC
B.PD,DC,BC,AB
C.PA,AD,PC,BC
D.PA,PB,PC,AD
6.下列四个图形中,是三棱锥的表面展开图的是( )
A.
B.
C.
D.
7.下列各图不是正方体表面展开图的是( )
A.
B.
C.
D.
8.如图,将长方体表面展开,下列选项中错误的是( )
A.
B.
C.
D.
9.下列图形是正方体表面积展开图的是( )
A.
B.
C.
D.
10.如图,在正方体的平面展开图中A、B两点间的距离为6,折成正方体后A、B两点是正方体的顶点,则这两个顶点的距离是( )
A.3
B.
C.6
D.3
二.填空题(共4小题)
11.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 .
12.如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有 种拼接方法.
13.已知一个圆柱的侧面展开图是如图所示的矩形,长为6π,宽为4π,那么这个圆柱底面圆的半径为 .
14.一个几何体的表面展开图如图所示,则这个几何体是 .
三.解答题(共6小题)
15.如图1所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图2所示,已知展开图中每个正方形的边长为1,
(1)求线段A′C′的长度;
(2)试比较立体图中∠BAC与展开图中∠B′A′C′的大小关系?并写出过程.
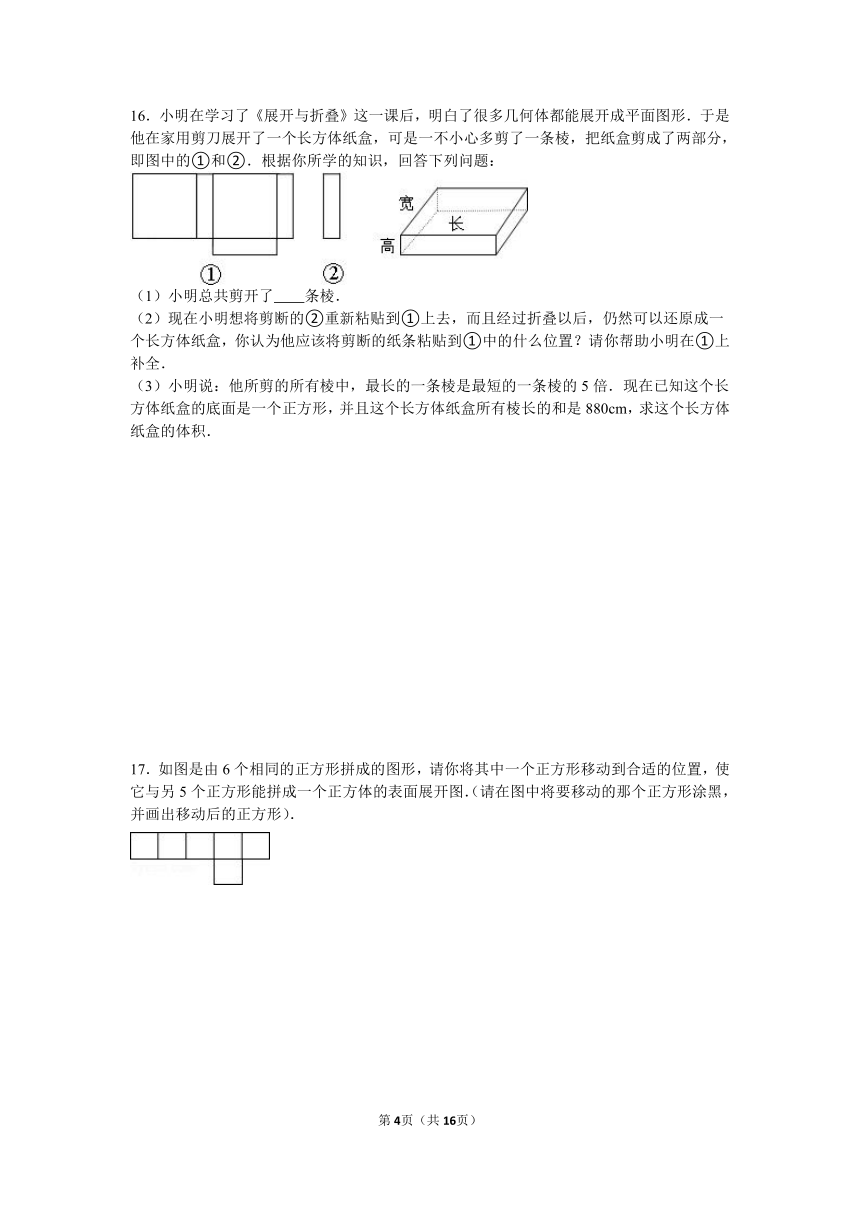
16.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
17.如图是由6个相同的正方形拼成的图形,请你将其中一个正方形移动到合适的位置,使它与另5个正方形能拼成一个正方体的表面展开图.(请在图中将要移动的那个正方形涂黑,并画出移动后的正方形).
18.如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注式子的值相等,求x的值.
19.如图①所示是一个长方体盒子,四边形ABCD是边长为a的正方形,DD′的长为b.
(1)写出与棱AB平行的所有的棱: ;
(2)求出该长方体的表面积(用含a、b的代数式表示);
(3)当a=40cm,b=20cm时,工人师傅用边长为c的正方形纸片(如图②)裁剪成六块,作为长方体的六个面,粘合成如图①所示的长方体.
①求出c的值;
②在图②中画出裁剪线的示意图,并标注相关的数据.
20.某正方体盒子,如图左边下方A处有一只蚂蚁,从A处爬行到侧棱GF上的中点M点处,如果蚂蚁爬行路线最短,请画出这条最短路线图.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 绍兴)如图是一个正方体,则它的表面展开图可以是( )
A.
B.
C.
D.
【分析】根据含有田字形和凹字形的图形不能折成正方体可判断A、C,D,故此可得到答案.
【解答】解:A、含有田字形,不能折成正方体,故A错误;
B、能折成正方体,故B正确;
C、凹字形,不能折成正方体,故C错误;
D、含有田字形,不能折成正方体,故D错误.
故选:B.
【点评】本题主要考查的是几何体的展开图,明确含有田字形和凹字形的图形不能折成正方体是解题的关键.
2.(2016 资阳)如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
A.
B.
C.
D.
【分析】根据几何体的展开图先判断出实心圆点与空心圆点的关系,进而可得出结论.
【解答】解:∵由图可知,实心圆点与空心圆点一定在紧相邻的三个侧面上,
∴C符合题意.
故选C.
【点评】本题考查的是几何体的展开图,此类问题从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
3.(2016 徐州)下列图形中,不可以作为一个正方体的展开图的是( )
A.
B.
C.
D.
【分析】利用不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况进行判断也可.
【解答】A.可以作为一个正方体的展开图,
B.可以作为一个正方体的展开图,
C.不可以作为一个正方体的展开图,
D.可以作为一个正方体的展开图,
故选;C.
【点评】本题考查了正方体的展开图,熟记展开图的11种形式是解题的关键,利用不是正方体展开图的“一线不过四、田凹应弃之”(即不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况)判断也可.
4.(2016 河南模拟)将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A.
B.
C.
D.
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.注意带图案的三个面相交于一点.
【解答】解:由原正方体知,带图案的三个面相交于一点,而通过折叠后A、B都不符合,且D折叠后图案的位置正好相反,所以能得到的图形是C.
故选C.
【点评】考查了几何体的展开图,解决此类问题,要充分考虑带有各种符号的面的特点及位置.
5.(2016 河南模拟)如图1所示,将一个正四棱锥(底面为正方形,四条测棱相等)的其中四条边剪开,得到图2,则被剪开的四条边有可能是( )
A.PA,PB,AD,BC
B.PD,DC,BC,AB
C.PA,AD,PC,BC
D.PA,PB,PC,AD
【分析】根据图2中正方形左边的三角形可知需剪开PA、PB,根据正方形右边三个三角形脱离正方形的上下两边可知需剪开AD、BC,可得答案.
【解答】解:根据图2中的展开图可知,底面正方形ABCD的左边一个三角形是独立的,
据此可知,需剪开图1中的PA、PB,
根据正方形右边三个三角形脱离正方形的上下两边可知,
需剪开AD、BC,
综上,被剪开的四条边可能是:PA、PB、AD、BC,
故选:A.
【点评】本题主要考查几何体的展开图,空间的想象力是基础,根据展开图逐步分解图形是解题的关键.
6.(2016 惠安县二模)下列四个图形中,是三棱锥的表面展开图的是( )
A.
B.
C.
D.
【分析】根据三棱锥的四个面都是三角形,还要能围成一个立体图形,进而分析得出即可.
【解答】解:A、能组成三棱锥,是;
B、不组成三棱锥,故不是;
C、组成的是三棱柱,故不是;
D、组成的是四棱锥,故不是;
故选A.
【点评】本题主要考查了三棱锥的表面展开图和空间想象能力,注意几何体的形状特点进而分析才行.
7.(2016 大东区二模)下列各图不是正方体表面展开图的是( )
A.
B.
C.
D.
【分析】由平面图形的折叠及正方体的展开图解题.
【解答】解:A,C,D是正方体的平面展开图,B有田字格,不是正方体的平面展开图,
故选:B.
【点评】本题考查了几何体的展开图.只要有“田”字格的展开图都不是正方体的表面展开图.
8.(2016 于田县校级模拟)如图,将长方体表面展开,下列选项中错误的是( )
A.
B.
C.
D.
【分析】长方体的表面展开图的特点,有四个长方形的侧面和上下两个底面组成.
【解答】解:A、是长方体平面展开图,不符合题意;
B、是长方体平面展开图,不符合题意;
C、有两个面重合,不是长方体平面展开图,不符合题意;
D、是长方体平面展开图,不符合题意.
故选:C.
【点评】本题考查的是长方体的展开图,关键是要注意上下底面的长和宽是否可以围成长方体.
9.(2016 长春校级一模)下列图形是正方体表面积展开图的是( )
A.
B.
C.
D.
【分析】根据正方体展开图的11种形式对各小题分析判断即可得解.
【解答】解:A、无法围成立方体,故此选项错误;
B、无法围成立方体,故此选项错误;
C、无法围成立方体,故此选项错误;
D、可以围成立方体,故此选项正确.
故选:D.
【点评】本题考查了正方体的展开图,熟记展开图的11种形式是解题的关键,利用不是正方体展开图的“一线不过四、田凹应弃之”(即不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况,)判断也可.
10.(2016 龙岩模拟)如图,在正方体的平面展开图中A、B两点间的距离为6,折成正方体后A、B两点是正方体的顶点,则这两个顶点的距离是( )
A.3
B.
C.6
D.3
【分析】根据这个平面展开图中的距离,求出正方体的棱长,进而得出正方体A、B两点间的距离即可.
【解答】解:∵AB=6,
∴把正方形组合起来之后会发现A、B在同一平面的对角线上,
∴该正方体A、B两点间的距离为3,
故选:D.
【点评】此题主要考查了几何体的展开图,根据正方体的展开图的特点求出正方体的棱长是解题关键.
二.填空题(共4小题)
11.(2016 云南)如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 144或384π .
【分析】分两种情况:①底面周长为6高为16π;②底面周长为16π高为6;先根据底面周长得到底面半径,再根据圆柱的体积公式计算即可求解.
【解答】解:①底面周长为6高为16π,
π×()2×16π
=π××16π
=144;
②底面周长为16π高为6,
π×()2×6
=π×64×6
=384π.
答:这个圆柱的体积可以是144或384π.
故答案为:144或384π.
【点评】本题考查了展开图折叠成几何体,本题关键是熟练掌握圆柱的体积公式,注意分类思想的运用.
12.(2016 市南区一模)如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有 4 种拼接方法.
【分析】结合正方体的平面展开图的特征,只要折叠后能围成正方体即可.
【解答】解:如图所示:
故小丽总共能有4种拼接方法.
故答案为:4.
【点评】此题主要考查了几何体的展开图.正方体的平面展开图共有11种,应灵活掌握,不能死记硬背.
13.(2015 桐庐县模拟)已知一个圆柱的侧面展开图是如图所示的矩形,长为6π,宽为4π,那么这个圆柱底面圆的半径为 2或3 .
【分析】分底面周长为4π和6π两种情况讨论,求得底面半径.
【解答】解:①底面周长为4π时,圆柱底面圆的半径为4π÷π÷2=2;
②底面周长为6π时,圆柱底面圆的半径为6π÷π÷2=1.
故答案为:2或3.
【点评】考查了圆柱的侧面展开图,注意分长为底面周长和宽为底面周长两种情况讨论求解.
14.(2015秋 玄武区期末)一个几何体的表面展开图如图所示,则这个几何体是 四棱锥 .
【分析】根据四棱锥的侧面展开图得出答案.
【解答】解:如图所示:这个几何体是四棱锥;
故答案为:四棱锥.
【点评】此题主要考查了几何体的展开图,熟记常见立体图形的平面展开图的特征是解决此类问题的关键.
三.解答题(共6小题)
15.(2016春 高阳县期末)如图1所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图2所示,已知展开图中每个正方形的边长为1,
(1)求线段A′C′的长度;
(2)试比较立体图中∠BAC与展开图中∠B′A′C′的大小关系?并写出过程.
【分析】(1)由长方形中最长的线段为对角线,从而可根据已知运用勾股定理求得最长线段的长;
(2)要确定角的大小关系,一般把两个角分别放在两个三角形中,然后根据三角形的特点或者全等或者相似形来解.
【解答】解:(1)如图(1)中的A′C′,在Rt△A′C′D′中,∵C′D′=1,A′D′=3,由勾股定理得,
∴
(2)∵立体图中∠BAC为平面等腰直角三角形的一锐角,
∴∠BAC=45°.
在平面展开图中,连接线段B′C′,由勾股定理可得:A'B'=,B'C'=.
又∵A′B′2+B′C′2=A′C′2,
由勾股定理的逆定理可得△A'B'C'为直角三角形.
又∵A′B′=B′C′,
∴△A′B′C′为等腰直角三角形.
∴∠B′A′C′=45°.
∴∠BAC与∠B′A′C′相等.
【点评】本题综合考查了展开与折叠,等腰直角三角形,勾股定理的知识,是一道综合性比较强的题,难度中等.
16.(2015秋 高邮市期末)小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 8 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
【分析】(1)根据平面图形得出剪开棱的条数,
(2)根据长方体的展开图的情况可知有两种情况,
(3)设最短的棱长高为acm,则长与宽相等为5acm,根据棱长的和是880cm,列出方程可求出长宽高,即可求出长方体纸盒的体积.
【解答】解(1)小明共剪了8条棱,
故答案为:8.
(2)如图,四种情况.
(3)∵长方体纸盒的底面是一个正方形,
∴设最短的棱长高为acm,则长与宽相等为5acm,
∵长方体纸盒所有棱长的和是880cm,
∴4(a+5a+5a)=880,解得a=20cm,
∴这个长方体纸盒的体积为:20×100×100=200000立方厘米.
【点评】本题主要考查了几何展开图,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
17.(2015秋 永登县期末)如图是由6个相同的正方形拼成的图形,请你将其中一个正方形移动到合适的位置,使它与另5个正方形能拼成一个正方体的表面展开图.(请在图中将要移动的那个正方形涂黑,并画出移动后的正方形).
【分析】根据题意可知,结合展开图中“1,4,1”格式作图,即可得出答案.
【解答】解:答案如下:
或
或等.
【点评】此题考查几何体的展开图,掌握正方体展开图的基本形式是解决问题的关键.
18.(2015秋 南昌校级期末)如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注式子的值相等,求x的值.
【分析】利用正方体及其表面展开图的特点,列出方程x﹣3=3x﹣2解答即可.
【解答】解:根据题意得,x﹣3=3x﹣2,
解得:x=﹣.
【点评】本题考查了正方体相对两个面上的文字.注意正方体的空间图形,从相对面入手,分析及解答问题.
19.(2015秋 南安市期末)如图①所示是一个长方体盒子,四边形ABCD是边长为a的正方形,DD′的长为b.
(1)写出与棱AB平行的所有的棱: A′B′,D′C′,DC ;
(2)求出该长方体的表面积(用含a、b的代数式表示);
(3)当a=40cm,b=20cm时,工人师傅用边长为c的正方形纸片(如图②)裁剪成六块,作为长方体的六个面,粘合成如图①所示的长方体.
①求出c的值;
②在图②中画出裁剪线的示意图,并标注相关的数据.
【分析】(1)根据长方体的特征填写即可;
(2)根据长方体的表面积公式即可求解;
(3)①根据长方体的表面积公式和正方形的面积公式即可求解;
②分成2个边长40cm的正方形,4个长40cm,宽20cm的长方形即可求解.
【解答】解:(1)与棱AB平行的所有的棱:A′B′,D′C′,DC.
故答案为:A′B′,D′C′,DC;
(2)长方体的表面积=2a2+4ab;
(3)①当a=40cm,b=20cm时,
2a2+4ab
=2×402+4×40×20
=3200+3200
=6400(cm2)
∵c2=2a2+4ab=6400,
∴c=80(
cm
);
②如下图所示:(注:答案不唯一,只要符合题意画一种即可)
【点评】考查了几何体的展开图,认识立体图形和几何体的表面积,本题考法较新颖,需要对长方体有充分的理解.
20.(2015秋 泾阳县期中)某正方体盒子,如图左边下方A处有一只蚂蚁,从A处爬行到侧棱GF上的中点M点处,如果蚂蚁爬行路线最短,请画出这条最短路线图.
【分析】要求正方体盒子中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.
【解答】解:如图,将正方体盒子中面ABCD和面CBFG展开成一个长方形,如图示,则A、M分别位于如图所示的位置,连接AM,即是这条最短路线图.
【点评】此题考查几何体的展开图,把正方体展开,根据两点之间线段最短解答即可.
第1页(共1页)
一.选择题(共10小题)
1.如图是一个正方体,则它的表面展开图可以是( )
A.
B.
C.
D.
2.如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
A.
B.
C.
D.
3.下列图形中,不可以作为一个正方体的展开图的是( )
A.
B.
C.
D.
4.将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A.
B.
C.
D.
5.如图1所示,将一个正四棱锥(底面为正方形,四条测棱相等)的其中四条边剪开,得到图2,则被剪开的四条边有可能是( )
A.PA,PB,AD,BC
B.PD,DC,BC,AB
C.PA,AD,PC,BC
D.PA,PB,PC,AD
6.下列四个图形中,是三棱锥的表面展开图的是( )
A.
B.
C.
D.
7.下列各图不是正方体表面展开图的是( )
A.
B.
C.
D.
8.如图,将长方体表面展开,下列选项中错误的是( )
A.
B.
C.
D.
9.下列图形是正方体表面积展开图的是( )
A.
B.
C.
D.
10.如图,在正方体的平面展开图中A、B两点间的距离为6,折成正方体后A、B两点是正方体的顶点,则这两个顶点的距离是( )
A.3
B.
C.6
D.3
二.填空题(共4小题)
11.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 .
12.如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有 种拼接方法.
13.已知一个圆柱的侧面展开图是如图所示的矩形,长为6π,宽为4π,那么这个圆柱底面圆的半径为 .
14.一个几何体的表面展开图如图所示,则这个几何体是 .
三.解答题(共6小题)
15.如图1所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图2所示,已知展开图中每个正方形的边长为1,
(1)求线段A′C′的长度;
(2)试比较立体图中∠BAC与展开图中∠B′A′C′的大小关系?并写出过程.
16.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
17.如图是由6个相同的正方形拼成的图形,请你将其中一个正方形移动到合适的位置,使它与另5个正方形能拼成一个正方体的表面展开图.(请在图中将要移动的那个正方形涂黑,并画出移动后的正方形).
18.如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注式子的值相等,求x的值.
19.如图①所示是一个长方体盒子,四边形ABCD是边长为a的正方形,DD′的长为b.
(1)写出与棱AB平行的所有的棱: ;
(2)求出该长方体的表面积(用含a、b的代数式表示);
(3)当a=40cm,b=20cm时,工人师傅用边长为c的正方形纸片(如图②)裁剪成六块,作为长方体的六个面,粘合成如图①所示的长方体.
①求出c的值;
②在图②中画出裁剪线的示意图,并标注相关的数据.
20.某正方体盒子,如图左边下方A处有一只蚂蚁,从A处爬行到侧棱GF上的中点M点处,如果蚂蚁爬行路线最短,请画出这条最短路线图.
参考答案与试题解析
一.选择题(共10小题)
1.(2016 绍兴)如图是一个正方体,则它的表面展开图可以是( )
A.
B.
C.
D.
【分析】根据含有田字形和凹字形的图形不能折成正方体可判断A、C,D,故此可得到答案.
【解答】解:A、含有田字形,不能折成正方体,故A错误;
B、能折成正方体,故B正确;
C、凹字形,不能折成正方体,故C错误;
D、含有田字形,不能折成正方体,故D错误.
故选:B.
【点评】本题主要考查的是几何体的展开图,明确含有田字形和凹字形的图形不能折成正方体是解题的关键.
2.(2016 资阳)如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
A.
B.
C.
D.
【分析】根据几何体的展开图先判断出实心圆点与空心圆点的关系,进而可得出结论.
【解答】解:∵由图可知,实心圆点与空心圆点一定在紧相邻的三个侧面上,
∴C符合题意.
故选C.
【点评】本题考查的是几何体的展开图,此类问题从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
3.(2016 徐州)下列图形中,不可以作为一个正方体的展开图的是( )
A.
B.
C.
D.
【分析】利用不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况进行判断也可.
【解答】A.可以作为一个正方体的展开图,
B.可以作为一个正方体的展开图,
C.不可以作为一个正方体的展开图,
D.可以作为一个正方体的展开图,
故选;C.
【点评】本题考查了正方体的展开图,熟记展开图的11种形式是解题的关键,利用不是正方体展开图的“一线不过四、田凹应弃之”(即不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况)判断也可.
4.(2016 河南模拟)将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A.
B.
C.
D.
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.注意带图案的三个面相交于一点.
【解答】解:由原正方体知,带图案的三个面相交于一点,而通过折叠后A、B都不符合,且D折叠后图案的位置正好相反,所以能得到的图形是C.
故选C.
【点评】考查了几何体的展开图,解决此类问题,要充分考虑带有各种符号的面的特点及位置.
5.(2016 河南模拟)如图1所示,将一个正四棱锥(底面为正方形,四条测棱相等)的其中四条边剪开,得到图2,则被剪开的四条边有可能是( )
A.PA,PB,AD,BC
B.PD,DC,BC,AB
C.PA,AD,PC,BC
D.PA,PB,PC,AD
【分析】根据图2中正方形左边的三角形可知需剪开PA、PB,根据正方形右边三个三角形脱离正方形的上下两边可知需剪开AD、BC,可得答案.
【解答】解:根据图2中的展开图可知,底面正方形ABCD的左边一个三角形是独立的,
据此可知,需剪开图1中的PA、PB,
根据正方形右边三个三角形脱离正方形的上下两边可知,
需剪开AD、BC,
综上,被剪开的四条边可能是:PA、PB、AD、BC,
故选:A.
【点评】本题主要考查几何体的展开图,空间的想象力是基础,根据展开图逐步分解图形是解题的关键.
6.(2016 惠安县二模)下列四个图形中,是三棱锥的表面展开图的是( )
A.
B.
C.
D.
【分析】根据三棱锥的四个面都是三角形,还要能围成一个立体图形,进而分析得出即可.
【解答】解:A、能组成三棱锥,是;
B、不组成三棱锥,故不是;
C、组成的是三棱柱,故不是;
D、组成的是四棱锥,故不是;
故选A.
【点评】本题主要考查了三棱锥的表面展开图和空间想象能力,注意几何体的形状特点进而分析才行.
7.(2016 大东区二模)下列各图不是正方体表面展开图的是( )
A.
B.
C.
D.
【分析】由平面图形的折叠及正方体的展开图解题.
【解答】解:A,C,D是正方体的平面展开图,B有田字格,不是正方体的平面展开图,
故选:B.
【点评】本题考查了几何体的展开图.只要有“田”字格的展开图都不是正方体的表面展开图.
8.(2016 于田县校级模拟)如图,将长方体表面展开,下列选项中错误的是( )
A.
B.
C.
D.
【分析】长方体的表面展开图的特点,有四个长方形的侧面和上下两个底面组成.
【解答】解:A、是长方体平面展开图,不符合题意;
B、是长方体平面展开图,不符合题意;
C、有两个面重合,不是长方体平面展开图,不符合题意;
D、是长方体平面展开图,不符合题意.
故选:C.
【点评】本题考查的是长方体的展开图,关键是要注意上下底面的长和宽是否可以围成长方体.
9.(2016 长春校级一模)下列图形是正方体表面积展开图的是( )
A.
B.
C.
D.
【分析】根据正方体展开图的11种形式对各小题分析判断即可得解.
【解答】解:A、无法围成立方体,故此选项错误;
B、无法围成立方体,故此选项错误;
C、无法围成立方体,故此选项错误;
D、可以围成立方体,故此选项正确.
故选:D.
【点评】本题考查了正方体的展开图,熟记展开图的11种形式是解题的关键,利用不是正方体展开图的“一线不过四、田凹应弃之”(即不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况,)判断也可.
10.(2016 龙岩模拟)如图,在正方体的平面展开图中A、B两点间的距离为6,折成正方体后A、B两点是正方体的顶点,则这两个顶点的距离是( )
A.3
B.
C.6
D.3
【分析】根据这个平面展开图中的距离,求出正方体的棱长,进而得出正方体A、B两点间的距离即可.
【解答】解:∵AB=6,
∴把正方形组合起来之后会发现A、B在同一平面的对角线上,
∴该正方体A、B两点间的距离为3,
故选:D.
【点评】此题主要考查了几何体的展开图,根据正方体的展开图的特点求出正方体的棱长是解题关键.
二.填空题(共4小题)
11.(2016 云南)如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 144或384π .
【分析】分两种情况:①底面周长为6高为16π;②底面周长为16π高为6;先根据底面周长得到底面半径,再根据圆柱的体积公式计算即可求解.
【解答】解:①底面周长为6高为16π,
π×()2×16π
=π××16π
=144;
②底面周长为16π高为6,
π×()2×6
=π×64×6
=384π.
答:这个圆柱的体积可以是144或384π.
故答案为:144或384π.
【点评】本题考查了展开图折叠成几何体,本题关键是熟练掌握圆柱的体积公式,注意分类思想的运用.
12.(2016 市南区一模)如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有 4 种拼接方法.
【分析】结合正方体的平面展开图的特征,只要折叠后能围成正方体即可.
【解答】解:如图所示:
故小丽总共能有4种拼接方法.
故答案为:4.
【点评】此题主要考查了几何体的展开图.正方体的平面展开图共有11种,应灵活掌握,不能死记硬背.
13.(2015 桐庐县模拟)已知一个圆柱的侧面展开图是如图所示的矩形,长为6π,宽为4π,那么这个圆柱底面圆的半径为 2或3 .
【分析】分底面周长为4π和6π两种情况讨论,求得底面半径.
【解答】解:①底面周长为4π时,圆柱底面圆的半径为4π÷π÷2=2;
②底面周长为6π时,圆柱底面圆的半径为6π÷π÷2=1.
故答案为:2或3.
【点评】考查了圆柱的侧面展开图,注意分长为底面周长和宽为底面周长两种情况讨论求解.
14.(2015秋 玄武区期末)一个几何体的表面展开图如图所示,则这个几何体是 四棱锥 .
【分析】根据四棱锥的侧面展开图得出答案.
【解答】解:如图所示:这个几何体是四棱锥;
故答案为:四棱锥.
【点评】此题主要考查了几何体的展开图,熟记常见立体图形的平面展开图的特征是解决此类问题的关键.
三.解答题(共6小题)
15.(2016春 高阳县期末)如图1所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图2所示,已知展开图中每个正方形的边长为1,
(1)求线段A′C′的长度;
(2)试比较立体图中∠BAC与展开图中∠B′A′C′的大小关系?并写出过程.
【分析】(1)由长方形中最长的线段为对角线,从而可根据已知运用勾股定理求得最长线段的长;
(2)要确定角的大小关系,一般把两个角分别放在两个三角形中,然后根据三角形的特点或者全等或者相似形来解.
【解答】解:(1)如图(1)中的A′C′,在Rt△A′C′D′中,∵C′D′=1,A′D′=3,由勾股定理得,
∴
(2)∵立体图中∠BAC为平面等腰直角三角形的一锐角,
∴∠BAC=45°.
在平面展开图中,连接线段B′C′,由勾股定理可得:A'B'=,B'C'=.
又∵A′B′2+B′C′2=A′C′2,
由勾股定理的逆定理可得△A'B'C'为直角三角形.
又∵A′B′=B′C′,
∴△A′B′C′为等腰直角三角形.
∴∠B′A′C′=45°.
∴∠BAC与∠B′A′C′相等.
【点评】本题综合考查了展开与折叠,等腰直角三角形,勾股定理的知识,是一道综合性比较强的题,难度中等.
16.(2015秋 高邮市期末)小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 8 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
【分析】(1)根据平面图形得出剪开棱的条数,
(2)根据长方体的展开图的情况可知有两种情况,
(3)设最短的棱长高为acm,则长与宽相等为5acm,根据棱长的和是880cm,列出方程可求出长宽高,即可求出长方体纸盒的体积.
【解答】解(1)小明共剪了8条棱,
故答案为:8.
(2)如图,四种情况.
(3)∵长方体纸盒的底面是一个正方形,
∴设最短的棱长高为acm,则长与宽相等为5acm,
∵长方体纸盒所有棱长的和是880cm,
∴4(a+5a+5a)=880,解得a=20cm,
∴这个长方体纸盒的体积为:20×100×100=200000立方厘米.
【点评】本题主要考查了几何展开图,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
17.(2015秋 永登县期末)如图是由6个相同的正方形拼成的图形,请你将其中一个正方形移动到合适的位置,使它与另5个正方形能拼成一个正方体的表面展开图.(请在图中将要移动的那个正方形涂黑,并画出移动后的正方形).
【分析】根据题意可知,结合展开图中“1,4,1”格式作图,即可得出答案.
【解答】解:答案如下:
或
或等.
【点评】此题考查几何体的展开图,掌握正方体展开图的基本形式是解决问题的关键.
18.(2015秋 南昌校级期末)如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注式子的值相等,求x的值.
【分析】利用正方体及其表面展开图的特点,列出方程x﹣3=3x﹣2解答即可.
【解答】解:根据题意得,x﹣3=3x﹣2,
解得:x=﹣.
【点评】本题考查了正方体相对两个面上的文字.注意正方体的空间图形,从相对面入手,分析及解答问题.
19.(2015秋 南安市期末)如图①所示是一个长方体盒子,四边形ABCD是边长为a的正方形,DD′的长为b.
(1)写出与棱AB平行的所有的棱: A′B′,D′C′,DC ;
(2)求出该长方体的表面积(用含a、b的代数式表示);
(3)当a=40cm,b=20cm时,工人师傅用边长为c的正方形纸片(如图②)裁剪成六块,作为长方体的六个面,粘合成如图①所示的长方体.
①求出c的值;
②在图②中画出裁剪线的示意图,并标注相关的数据.
【分析】(1)根据长方体的特征填写即可;
(2)根据长方体的表面积公式即可求解;
(3)①根据长方体的表面积公式和正方形的面积公式即可求解;
②分成2个边长40cm的正方形,4个长40cm,宽20cm的长方形即可求解.
【解答】解:(1)与棱AB平行的所有的棱:A′B′,D′C′,DC.
故答案为:A′B′,D′C′,DC;
(2)长方体的表面积=2a2+4ab;
(3)①当a=40cm,b=20cm时,
2a2+4ab
=2×402+4×40×20
=3200+3200
=6400(cm2)
∵c2=2a2+4ab=6400,
∴c=80(
cm
);
②如下图所示:(注:答案不唯一,只要符合题意画一种即可)
【点评】考查了几何体的展开图,认识立体图形和几何体的表面积,本题考法较新颖,需要对长方体有充分的理解.
20.(2015秋 泾阳县期中)某正方体盒子,如图左边下方A处有一只蚂蚁,从A处爬行到侧棱GF上的中点M点处,如果蚂蚁爬行路线最短,请画出这条最短路线图.
【分析】要求正方体盒子中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.
【解答】解:如图,将正方体盒子中面ABCD和面CBFG展开成一个长方形,如图示,则A、M分别位于如图所示的位置,连接AM,即是这条最短路线图.
【点评】此题考查几何体的展开图,把正方体展开,根据两点之间线段最短解答即可.
第1页(共1页)
