1.3.3 整数指数幂的运算法则 课件
文档属性
| 名称 | 1.3.3 整数指数幂的运算法则 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 548.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-20 15:34:35 | ||
图片预览





文档简介
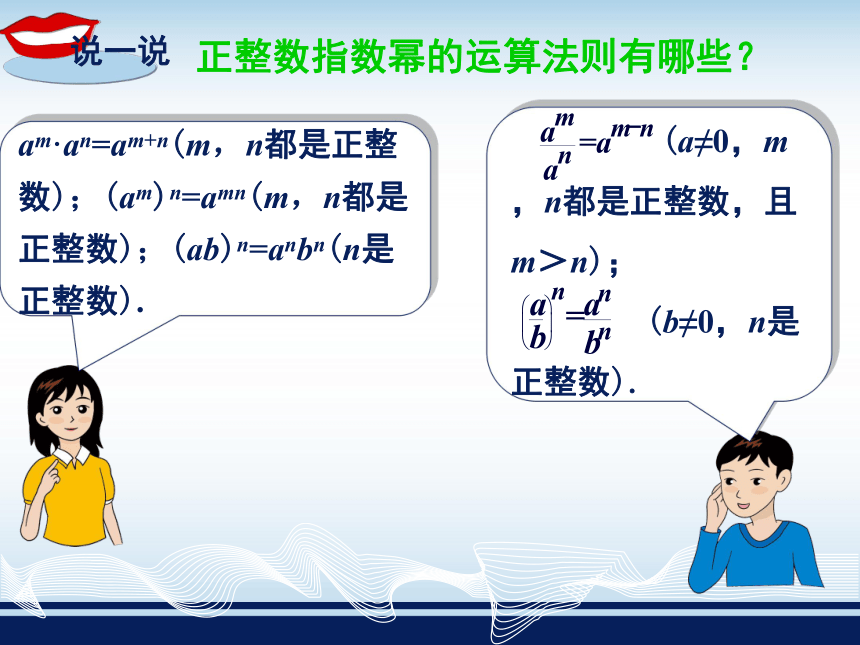
课件13张PPT。整数指数幂的运算法则学习目标1.掌握几种整数指数幂的运算法则并能用字母表示;2.理解每个公式成立的前提条件;3.灵活运用各公式进行计算;4.会“变形用”或“逆用”公式;正整数指数幂的运算法则有哪些?am·an=am+n(m,n都是正整数);(am)n=amn(m,n都是正整数);(ab)n=anbn(n是正整数).思考:之前我们已经学习了零次幂和负整数指数幂的运算,那么 am·an=am+n(m,n都是正整数)这条性质能否扩大到m,n都是任意整数的情形.?am · an=am+n(a≠0,m,n都是整数),由此可以得出:同底数幂相乘:思考:
其他的性质能否也扩大到m,n都是任意整数的情形?分析:
通过验证,其他的性质在m,n为任意整数时都成立. 由于对于a≠0,m,n都是整数,有: 因此同底数幂相除的运算法则被包含在同底数幂相乘的公式中. am · an=am+n(a≠0,m,n都是整数), 由于对于a≠0,b≠0,n是整数,有 因此分式的乘方的运算法则被包含在积的乘方公式中.(ab)n=anbn(a≠0,b≠0,n是整数)am · an=am+n(a≠0,m,n都是整数),(am)n=amn(a≠0,m,n都是整数),(ab)n=anbn(a≠0,b≠0,n是整数).所以,整数指数幂的运算公式可以归纳为以下三个:①②③例1 设a≠0,b≠0,计算下列各式:
(1)a7 · a-3; (2)(a-3)-2; (3)a3b(a-1b)-2.解= a7+(-3)解= a(-3)×(-2)= a4= a6 解= a3b·a2b-2= a3+2b1+(-2)= a5b-1 注意:
最后结果一般不保留负指数,应写成分式形式.例2 计算下列各式:点拔:分式形式的幂运算,若分式外面有幂要先算分式的乘方,再将分子、分母的系数,同底数幂分别相除,对于只在分子或分母里出现的字母或式子在分式里照写. 1. 设a≠0,b≠0,计算下列各式:(4)a-5(a2b-1)3; 2. 计算下列各式: (1)同底数幂相乘:am · an=am+n(a≠0,m,n都是整数),(2)幂的乘方:(am)n=amn(a≠0,m,n都是整数),(3)积的乘方:(ab)n=anbn(a≠0,b≠0,n是整数).整数指数幂的运算公式
其他的性质能否也扩大到m,n都是任意整数的情形?分析:
通过验证,其他的性质在m,n为任意整数时都成立. 由于对于a≠0,m,n都是整数,有: 因此同底数幂相除的运算法则被包含在同底数幂相乘的公式中. am · an=am+n(a≠0,m,n都是整数), 由于对于a≠0,b≠0,n是整数,有 因此分式的乘方的运算法则被包含在积的乘方公式中.(ab)n=anbn(a≠0,b≠0,n是整数)am · an=am+n(a≠0,m,n都是整数),(am)n=amn(a≠0,m,n都是整数),(ab)n=anbn(a≠0,b≠0,n是整数).所以,整数指数幂的运算公式可以归纳为以下三个:①②③例1 设a≠0,b≠0,计算下列各式:
(1)a7 · a-3; (2)(a-3)-2; (3)a3b(a-1b)-2.解= a7+(-3)解= a(-3)×(-2)= a4= a6 解= a3b·a2b-2= a3+2b1+(-2)= a5b-1 注意:
最后结果一般不保留负指数,应写成分式形式.例2 计算下列各式:点拔:分式形式的幂运算,若分式外面有幂要先算分式的乘方,再将分子、分母的系数,同底数幂分别相除,对于只在分子或分母里出现的字母或式子在分式里照写. 1. 设a≠0,b≠0,计算下列各式:(4)a-5(a2b-1)3; 2. 计算下列各式: (1)同底数幂相乘:am · an=am+n(a≠0,m,n都是整数),(2)幂的乘方:(am)n=amn(a≠0,m,n都是整数),(3)积的乘方:(ab)n=anbn(a≠0,b≠0,n是整数).整数指数幂的运算公式
同课章节目录
