2.5.2 矩形的判定课件1(17张PPT)
文档属性
| 名称 | 2.5.2 矩形的判定课件1(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 297.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-20 00:00:00 | ||
图片预览





文档简介
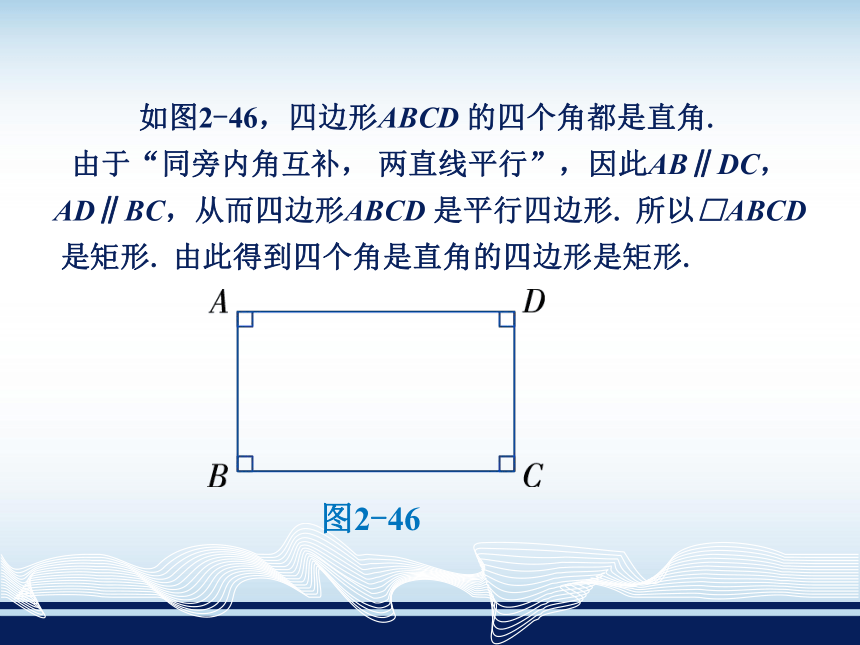
课件17张PPT。2.5矩 形——2.5.2 矩形的判定矩形的四个角是直角,那么,四个角是直角的四边形是矩形吗?三个角是直角呢?两个角是直角呢?如图2-46,四边形ABCD 的四个角都是直角.
由于“同旁内角互补, 两直线平行”,因此AB∥DC, AD∥BC,从而四边形ABCD 是平行四边形. 所以□ABCD
是矩形. 由此得到四个角是直角的四边形是矩形.图2-46三个角是直角的四边形是矩形. 三个角是直角的四边形,容易知道另一个角也
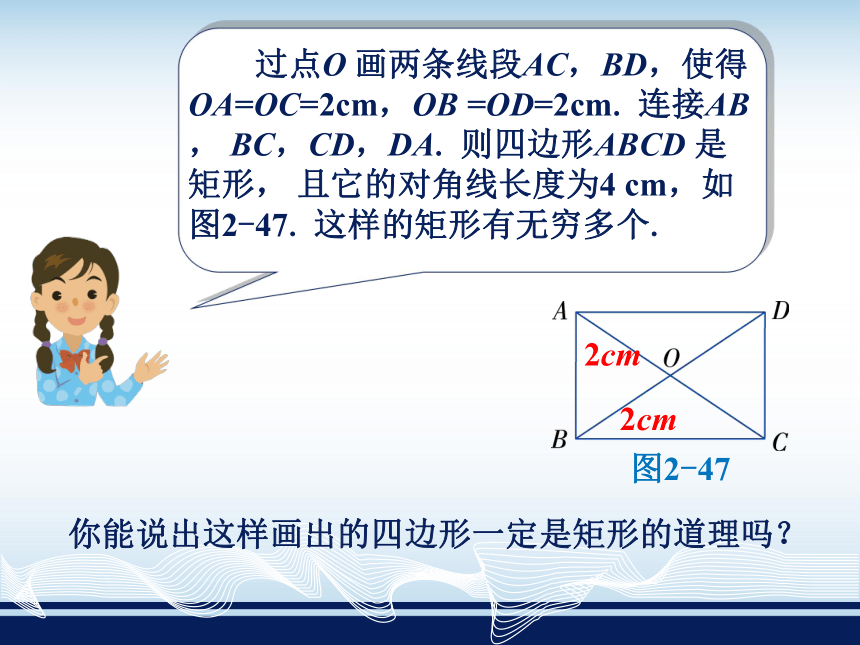
是直角,由此得到: 从“矩形的对角线相等且互相平分”这一性质受到启发,你能画出对角线长度为4cm的一个矩形吗?这样的矩形有多少个?你能说出这样画出的四边形一定是矩形的道理吗? 如图2-47,由画法可知,四边形ABCD的两条对角线互相平分,因此它是平行四边形,又已知其对角线相等,上述问题抽象出来就是:对角线相等的平行四边形是矩形吗?我们来进行证明.在□ABCD中,由于AB=DC,AC=DB,BC=CB,因此 △ABC≌△DCB. (SSS)从而 ∠ABC=∠DCB.又∠ABC+∠DCB =180°,于是 ∠ABC=90°.所以 □ABCD是矩形.图2-47对角线相等的平行四边形是矩形.由此得到矩形的判定定理:对角线相等的四边形是矩形吗?图2-48(2) ∵ △OBC是等腰三角形,其中OB = OC, ∴ AC与DB相等且互相平分.∴ △OBC是等腰三角形.∴ AC = 2OC = 2OB = BD.∴ □ABCD是矩形.图2-481. 如图,在四边形ABCD中,∠A=∠B=∠C=∠D,
求证:四边形ABCD是矩形.证明:因为四边形中,∠A=∠B=∠C=∠D ,
四边形的内角和为360°,
所以∠A=∠B=∠C=∠D= 90° ,
所以四边形ABCD是矩形.
(三个角是直角的四边形是矩形.)2. 如图,在□ABCD中,对角线AC,BD相交于点O, ∠AOB = 60°,AB= 2,AC= 4,求□ABCD的面积.∴ △OAB是等腰三角形.∴ △OAB是等边三角形.
又∠AOB = 60°,∴ OA=OB=2, ∴ AC=BD=4.∴ □ABCD是矩形.
(对角线相等的平行四边形是矩形.)
作OE⊥AD于点E.E例 在四边形ABCD中,对角线AC与BD互相平分,交点为O,在不添加任何辅助线的前提下,要使四边形ABCD成为矩形,还需添加一个条件,这个条件可以是
.AC=BD 或 ∠ABC,∠CDA,∠BAD,∠BCD之中有任一个角为直角结 束
由于“同旁内角互补, 两直线平行”,因此AB∥DC, AD∥BC,从而四边形ABCD 是平行四边形. 所以□ABCD
是矩形. 由此得到四个角是直角的四边形是矩形.图2-46三个角是直角的四边形是矩形. 三个角是直角的四边形,容易知道另一个角也
是直角,由此得到: 从“矩形的对角线相等且互相平分”这一性质受到启发,你能画出对角线长度为4cm的一个矩形吗?这样的矩形有多少个?你能说出这样画出的四边形一定是矩形的道理吗? 如图2-47,由画法可知,四边形ABCD的两条对角线互相平分,因此它是平行四边形,又已知其对角线相等,上述问题抽象出来就是:对角线相等的平行四边形是矩形吗?我们来进行证明.在□ABCD中,由于AB=DC,AC=DB,BC=CB,因此 △ABC≌△DCB. (SSS)从而 ∠ABC=∠DCB.又∠ABC+∠DCB =180°,于是 ∠ABC=90°.所以 □ABCD是矩形.图2-47对角线相等的平行四边形是矩形.由此得到矩形的判定定理:对角线相等的四边形是矩形吗?图2-48(2) ∵ △OBC是等腰三角形,其中OB = OC, ∴ AC与DB相等且互相平分.∴ △OBC是等腰三角形.∴ AC = 2OC = 2OB = BD.∴ □ABCD是矩形.图2-481. 如图,在四边形ABCD中,∠A=∠B=∠C=∠D,
求证:四边形ABCD是矩形.证明:因为四边形中,∠A=∠B=∠C=∠D ,
四边形的内角和为360°,
所以∠A=∠B=∠C=∠D= 90° ,
所以四边形ABCD是矩形.
(三个角是直角的四边形是矩形.)2. 如图,在□ABCD中,对角线AC,BD相交于点O, ∠AOB = 60°,AB= 2,AC= 4,求□ABCD的面积.∴ △OAB是等腰三角形.∴ △OAB是等边三角形.
又∠AOB = 60°,∴ OA=OB=2, ∴ AC=BD=4.∴ □ABCD是矩形.
(对角线相等的平行四边形是矩形.)
作OE⊥AD于点E.E例 在四边形ABCD中,对角线AC与BD互相平分,交点为O,在不添加任何辅助线的前提下,要使四边形ABCD成为矩形,还需添加一个条件,这个条件可以是
.AC=BD 或 ∠ABC,∠CDA,∠BAD,∠BCD之中有任一个角为直角结 束
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
