3.3 轴对称和平移的坐标表示课件2(25张PPT)
文档属性
| 名称 | 3.3 轴对称和平移的坐标表示课件2(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-20 16:58:09 | ||
图片预览

文档简介
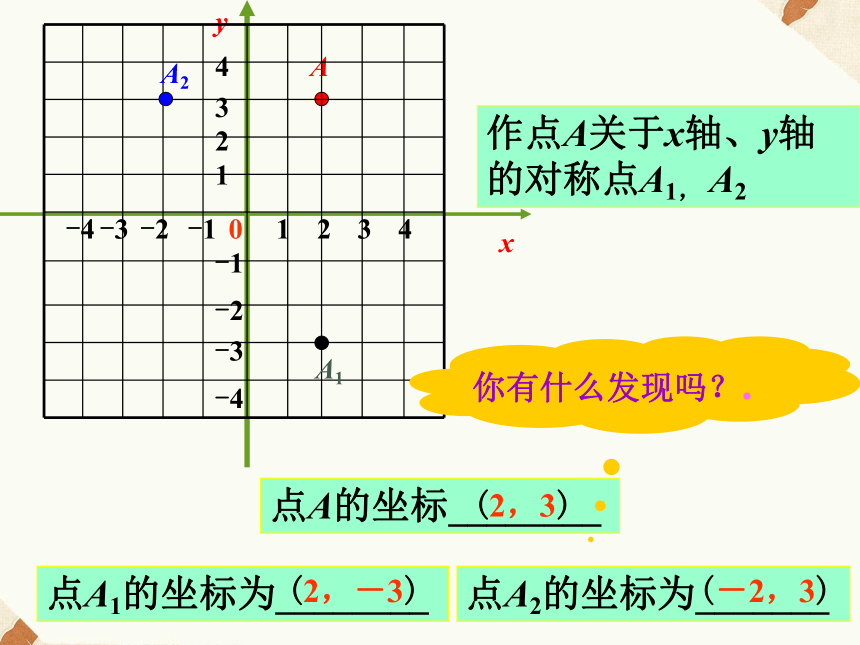
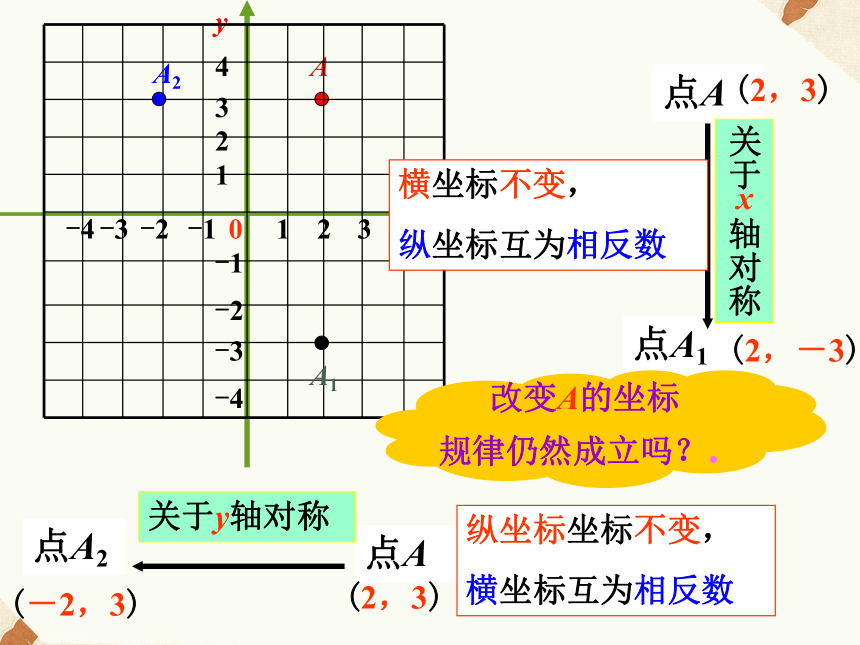
课件25张PPT。3.3轴对称和平移的坐标表示1 xy点A的坐标________(2,3)作点A关于x轴、y轴的对称点A1, A22 3 4 1 2 3 4 -1 -2 -3 -4 -4 -3 -2 -1 0 A2A1点A1的坐标为________点A2的坐标为_______(2,-3)(-2,3)你有什么发现吗?.1 Axy点A(2,3)2 3 4 1 2 3 4 -1 -2 -3 -4 -4 -3 -2 -1 0 A2A1点A1点A2(2,-3)(-2,3)关于 轴对称x点A(2,3)关于y轴对称横坐标不变,
纵坐标互为相反数改变A的坐标
规律仍然成立吗?.纵坐标坐标不变,
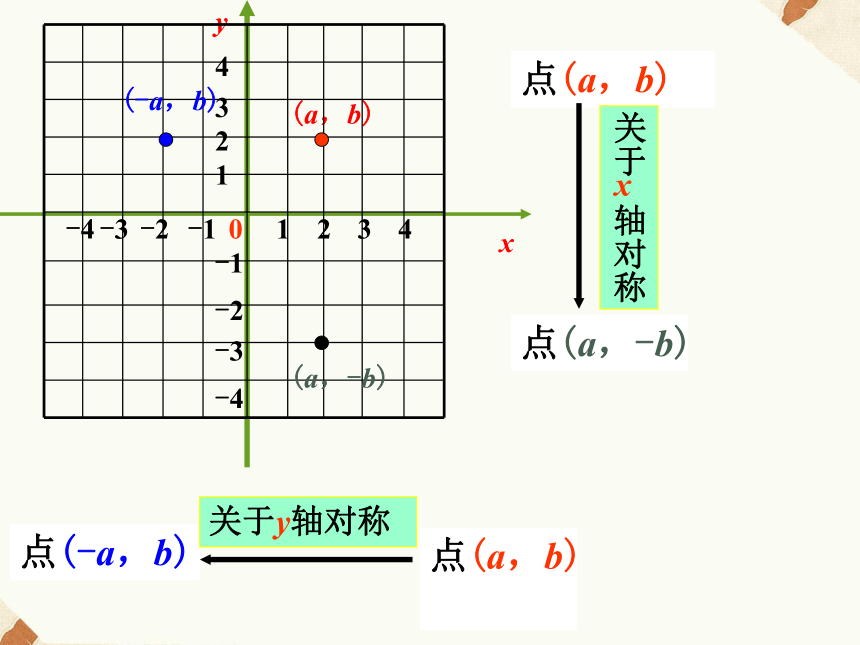
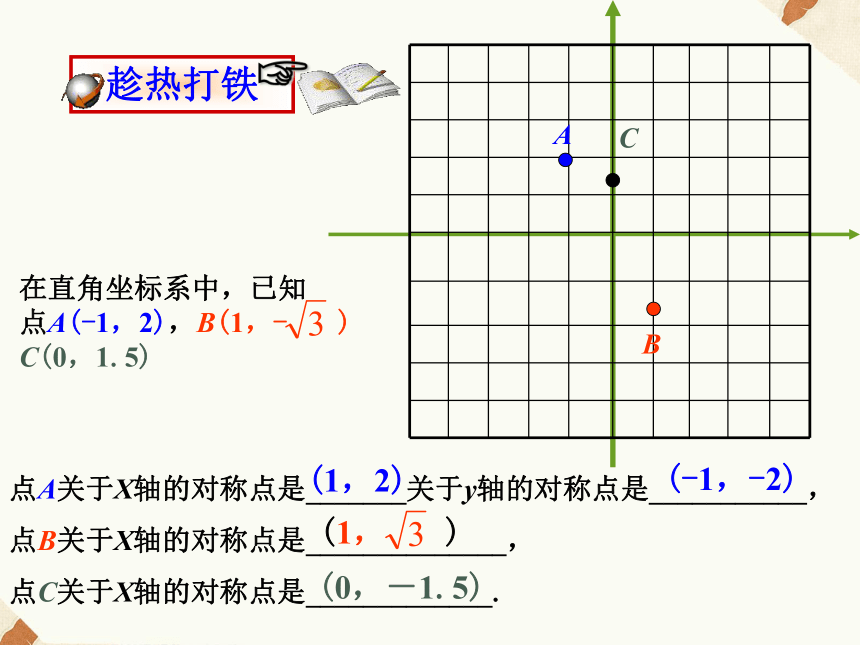
横坐标互为相反数1 (a,b)xy点(a,b)2 3 4 1 2 3 4 -1 -2 -3 -4 -4 -3 -2 -1 0 (-a,b)(a,-b)点(a,-b)点(-a,b)关于 轴对称x点(a,b)关于y轴对称ABC在直角坐标系中,已知
点A(-1,2),B(1,- )
C(0,1.5)点A关于X轴的对称点是_______关于y轴的对称点是___________,
点B关于X轴的对称点是______________,
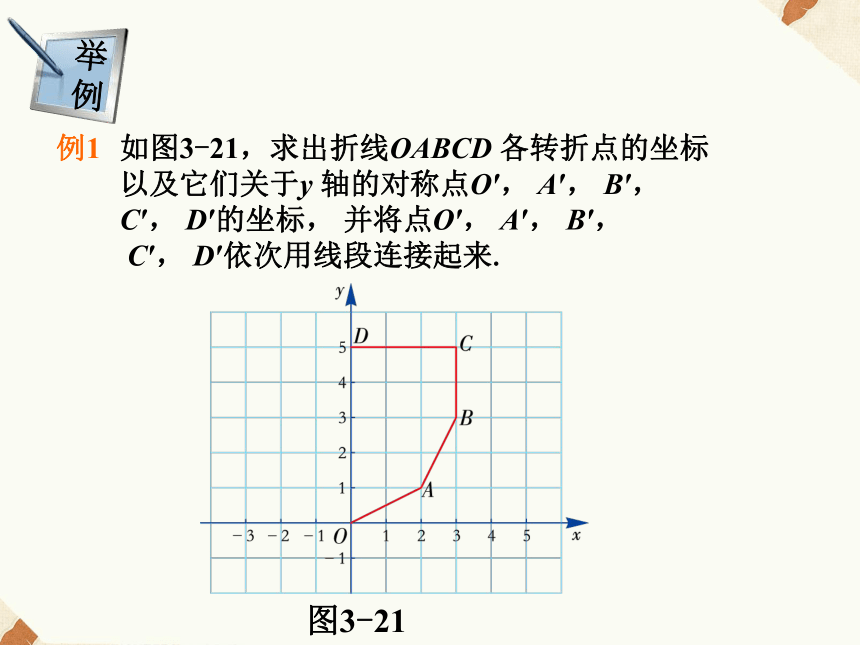
点C关于X轴的对称点是_____________.(1,2)(-1,-2)(1, )(0,-1.5)图3-21(1)求出?ABC各顶点的坐标,
以及它们关于y轴的对称点的
坐标并描点.
(2)将?ABC以y轴为对称轴作
一次轴对称变换,然后将所得的
像连同原图形,以x轴为对称轴
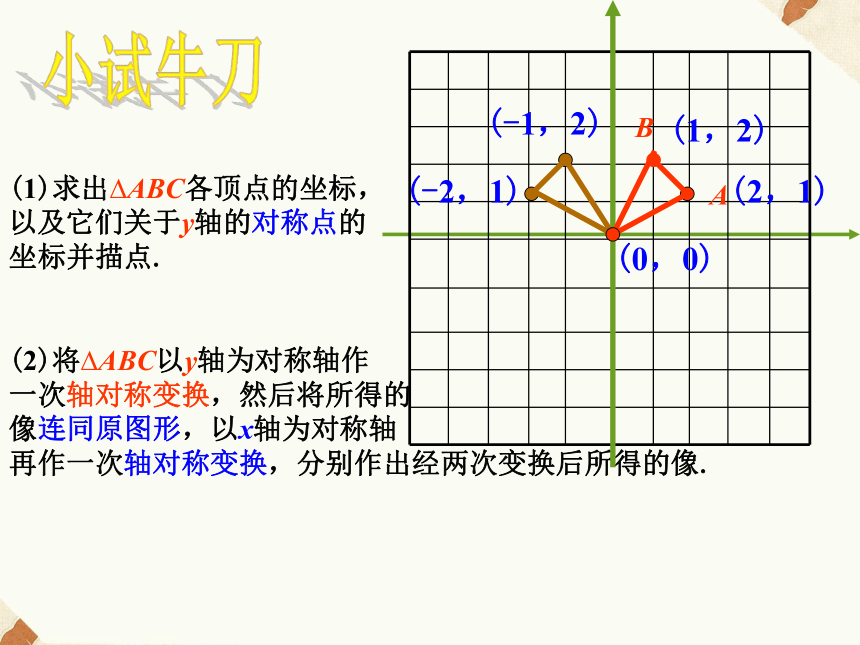
再作一次轴对称变换,分别作出经两次变换后所得的像.小试牛刀AB(1,2)(2,1)(-2,1)(-1,2)(0,0)(1)求出?ABC各顶点的坐标,
以及它们关于y轴的对称点的
坐标并描点.
(2)将?ABC以y轴为对称轴作
一次轴对称变换,然后将所得的
像连同原图形,以x轴为对称轴
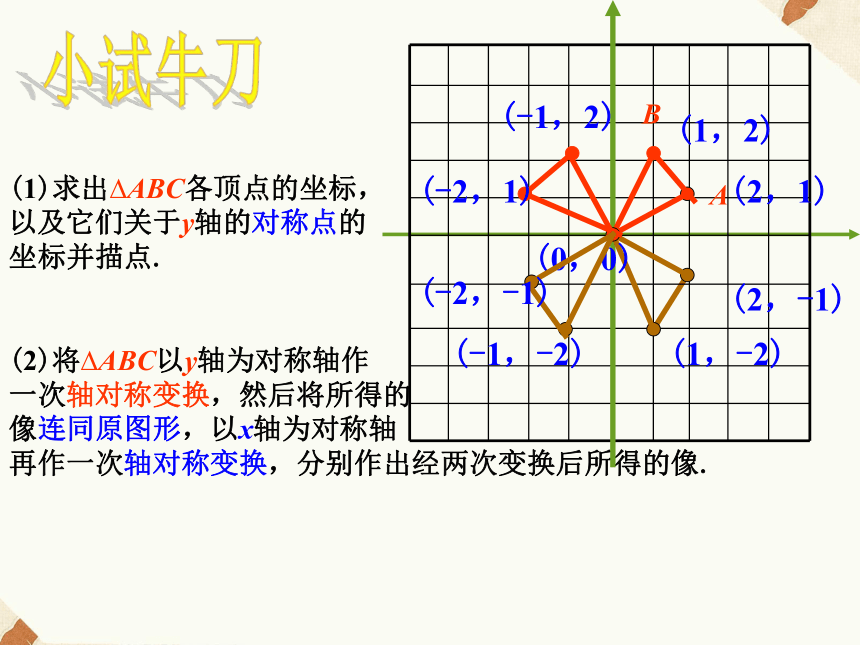
再作一次轴对称变换,分别作出经两次变换后所得的像.小试牛刀AB(1,-2)(2,1)(1,2)(-1,-2)(0,0)(-1,2)(-2,1)(-2,-1)(2,-1)将?ABC各顶点的横坐标,
纵坐标分别乘以-1,得到的
图形与原图形相比有什么变化?
AB(2,2)(4,0)(-2,-2)(0,0)O(-4,0)这一过程,可以看成一个什么变换?能力大比拼 1 xy(-3,3)作点A关于x轴、y轴的对称点A1, A22 3 4 1 2 3 4 -1 -2 -3 -4 -4 -3 -2 -1 0 A1A2可以利用其他的图形变换吗?A探究平移变换将点A(-3,3)、 B(4,5)分别作以下平移变换,作除相应的像,并写出像的坐标.2 4 -2 -4 0 BA合作学习-2 2 4 向上平移3个单位(____,____)(____,____)
向左平移5个单位A(-3,3)
B(4,5)
(____,____)向右平移5个单位
(____,____)A(-3,3)B(4,5)向下平移3个单位A12 3B1-1 5 A2-3 6 4 2 B2比较各点平移时的坐标变化,填在表格内.合作学习向上平移3个单位(____,____)(____,____)
向左平移5个单位A(-3,3)
B(4,5)
(____,____)向右平移5个单位
(____,____)A(-3,3)B(4,5)向下平移3个单位2 3-1 5 -3 6 4 2 坐标变化+5 不变 -5 不变 不变 不变 +3 -3 你能发现平移时坐标变化的规律吗?(1)左右平移时:
(a,b) 向右平移h个单位(a+h, b)(a,b) 向左平移h个单位(a-h, b)(2)上下平移时:
(a,b) 向上平移h个单位(a, b+h)向下平移h个单位(a, b -h )(a,b) 平移时的坐标变化图3-25依次连接点A1,B1,C1,即
可得△ABC的像△A1B1C1.依次连接点A2,B2,C2 , 即可得△ABC 的像△A2B2C2 .图3-26A 2 0 2 4 -2 B 1 分别求出A,A′的坐标;
B,B′的坐标,比较A与A′
B与B′之间的坐标变化.A′ B′ 变、变、变-4 -6 -8 -4 -2 4 6 2 从图形甲到图形乙可以看作经过怎样的图形变换?A(-8,-1)A′(-3,4)B(-3,-1)
B′(2,4)
先向右平移5个单位再向上平移5个单位可以看作只经过一次平移变换吗?.甲
乙
A 2 0 2 4 -2 B 1 分别求出A,A′的坐标;
B,B′的坐标,比较A与A′
B与B′之间的坐标变化.A′ B′ 变、变、变-4 -6 -8 -4 -2 4 6 2 从图形甲到图形乙可以看作经过怎样的图形变换?A(-8,-1)A′(-3,4)B(-3,-1)
B′(2,4)
先向右平移5个单位再向上平移5个单位可以看作只经过一次平移变换吗?.A 2 0 2 4 -2 B 平移图甲,使点A移至O点,求点B的对应点的坐标.A′ B′ 变、变、变-4 -6 -8 -4 -2 4 6 A(-8,-1)
B′(5,0)甲
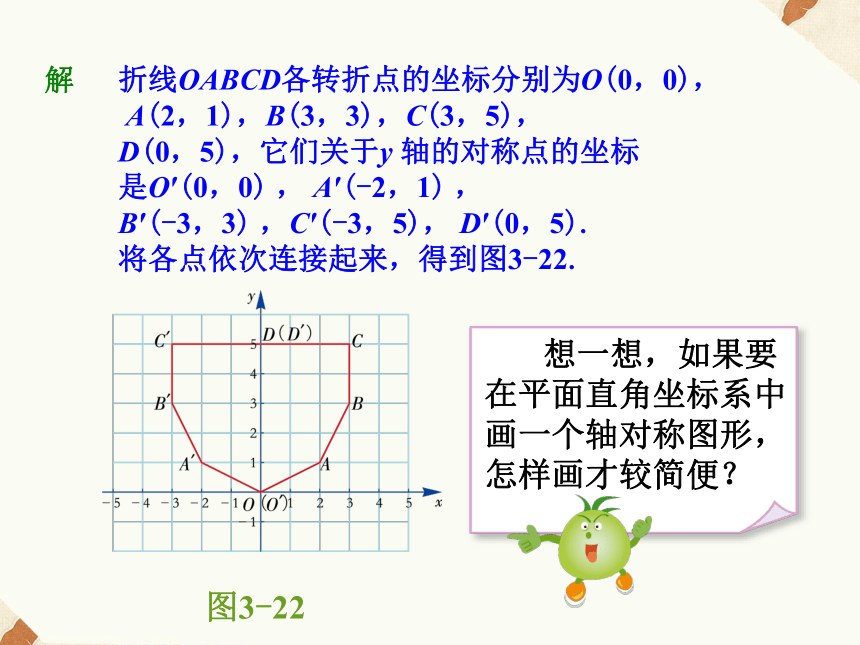
图3-29按照这个关系,由点A,B, C, D的坐标可知其像
的坐标分别是A′(-5,-3), B′(-3,-4),
C′(-1,-3), D′(-3,-1). 依次连接点
A′, B′, C′, D′,即得四边形A′B′ C′ D′ ,
如图3-29.1.已知点A的坐标为(-2,-3),分别求点经下列平移变换后所得的像的坐标.(1)向上平移3个单位 (2)向下平移3个单位(3)向左平移2个单位 (4)向右平移4个单位2.已知点A的坐标为(a,b), 点A经怎样变换得到下列点?(1) (a-2,b) (2) (a,b+2) (-2, 0)(-2, -6)(-4, -3)(2, -3)向左平移2个单位向上平移2个单位(5)先向右平移3个单位,再向下平移3个单位.(1, -6)小试牛刀(1)把点P(-2,7) 向左平移2个单位,得点_______.
(2)把点P(-2,7)向下平移7个单位,得点_______.
(3)把以 (-2,7)、(-2,2)为端点的线段向右平移7个单位,所得像上任意一点的坐标可表示为_______(-4, 7)(-2, 0)(5, y)(2≤y ≤7)
纵坐标互为相反数改变A的坐标
规律仍然成立吗?.纵坐标坐标不变,
横坐标互为相反数1 (a,b)xy点(a,b)2 3 4 1 2 3 4 -1 -2 -3 -4 -4 -3 -2 -1 0 (-a,b)(a,-b)点(a,-b)点(-a,b)关于 轴对称x点(a,b)关于y轴对称ABC在直角坐标系中,已知
点A(-1,2),B(1,- )
C(0,1.5)点A关于X轴的对称点是_______关于y轴的对称点是___________,
点B关于X轴的对称点是______________,
点C关于X轴的对称点是_____________.(1,2)(-1,-2)(1, )(0,-1.5)图3-21(1)求出?ABC各顶点的坐标,
以及它们关于y轴的对称点的
坐标并描点.
(2)将?ABC以y轴为对称轴作
一次轴对称变换,然后将所得的
像连同原图形,以x轴为对称轴
再作一次轴对称变换,分别作出经两次变换后所得的像.小试牛刀AB(1,2)(2,1)(-2,1)(-1,2)(0,0)(1)求出?ABC各顶点的坐标,
以及它们关于y轴的对称点的
坐标并描点.
(2)将?ABC以y轴为对称轴作
一次轴对称变换,然后将所得的
像连同原图形,以x轴为对称轴
再作一次轴对称变换,分别作出经两次变换后所得的像.小试牛刀AB(1,-2)(2,1)(1,2)(-1,-2)(0,0)(-1,2)(-2,1)(-2,-1)(2,-1)将?ABC各顶点的横坐标,
纵坐标分别乘以-1,得到的
图形与原图形相比有什么变化?
AB(2,2)(4,0)(-2,-2)(0,0)O(-4,0)这一过程,可以看成一个什么变换?能力大比拼 1 xy(-3,3)作点A关于x轴、y轴的对称点A1, A22 3 4 1 2 3 4 -1 -2 -3 -4 -4 -3 -2 -1 0 A1A2可以利用其他的图形变换吗?A探究平移变换将点A(-3,3)、 B(4,5)分别作以下平移变换,作除相应的像,并写出像的坐标.2 4 -2 -4 0 BA合作学习-2 2 4 向上平移3个单位(____,____)(____,____)
向左平移5个单位A(-3,3)
B(4,5)
(____,____)向右平移5个单位
(____,____)A(-3,3)B(4,5)向下平移3个单位A12 3B1-1 5 A2-3 6 4 2 B2比较各点平移时的坐标变化,填在表格内.合作学习向上平移3个单位(____,____)(____,____)
向左平移5个单位A(-3,3)
B(4,5)
(____,____)向右平移5个单位
(____,____)A(-3,3)B(4,5)向下平移3个单位2 3-1 5 -3 6 4 2 坐标变化+5 不变 -5 不变 不变 不变 +3 -3 你能发现平移时坐标变化的规律吗?(1)左右平移时:
(a,b) 向右平移h个单位(a+h, b)(a,b) 向左平移h个单位(a-h, b)(2)上下平移时:
(a,b) 向上平移h个单位(a, b+h)向下平移h个单位(a, b -h )(a,b) 平移时的坐标变化图3-25依次连接点A1,B1,C1,即
可得△ABC的像△A1B1C1.依次连接点A2,B2,C2 , 即可得△ABC 的像△A2B2C2 .图3-26A 2 0 2 4 -2 B 1 分别求出A,A′的坐标;
B,B′的坐标,比较A与A′
B与B′之间的坐标变化.A′ B′ 变、变、变-4 -6 -8 -4 -2 4 6 2 从图形甲到图形乙可以看作经过怎样的图形变换?A(-8,-1)A′(-3,4)B(-3,-1)
B′(2,4)
先向右平移5个单位再向上平移5个单位可以看作只经过一次平移变换吗?.甲
乙
A 2 0 2 4 -2 B 1 分别求出A,A′的坐标;
B,B′的坐标,比较A与A′
B与B′之间的坐标变化.A′ B′ 变、变、变-4 -6 -8 -4 -2 4 6 2 从图形甲到图形乙可以看作经过怎样的图形变换?A(-8,-1)A′(-3,4)B(-3,-1)
B′(2,4)
先向右平移5个单位再向上平移5个单位可以看作只经过一次平移变换吗?.A 2 0 2 4 -2 B 平移图甲,使点A移至O点,求点B的对应点的坐标.A′ B′ 变、变、变-4 -6 -8 -4 -2 4 6 A(-8,-1)
B′(5,0)甲
图3-29按照这个关系,由点A,B, C, D的坐标可知其像
的坐标分别是A′(-5,-3), B′(-3,-4),
C′(-1,-3), D′(-3,-1). 依次连接点
A′, B′, C′, D′,即得四边形A′B′ C′ D′ ,
如图3-29.1.已知点A的坐标为(-2,-3),分别求点经下列平移变换后所得的像的坐标.(1)向上平移3个单位 (2)向下平移3个单位(3)向左平移2个单位 (4)向右平移4个单位2.已知点A的坐标为(a,b), 点A经怎样变换得到下列点?(1) (a-2,b) (2) (a,b+2) (-2, 0)(-2, -6)(-4, -3)(2, -3)向左平移2个单位向上平移2个单位(5)先向右平移3个单位,再向下平移3个单位.(1, -6)小试牛刀(1)把点P(-2,7) 向左平移2个单位,得点_______.
(2)把点P(-2,7)向下平移7个单位,得点_______.
(3)把以 (-2,7)、(-2,2)为端点的线段向右平移7个单位,所得像上任意一点的坐标可表示为_______(-4, 7)(-2, 0)(5, y)(2≤y ≤7)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
