4.1.1 变量与函数 课件2

课件15张PPT。 4.1.1 变量与函数如图是某地一天内的气温变化图 看图回答：
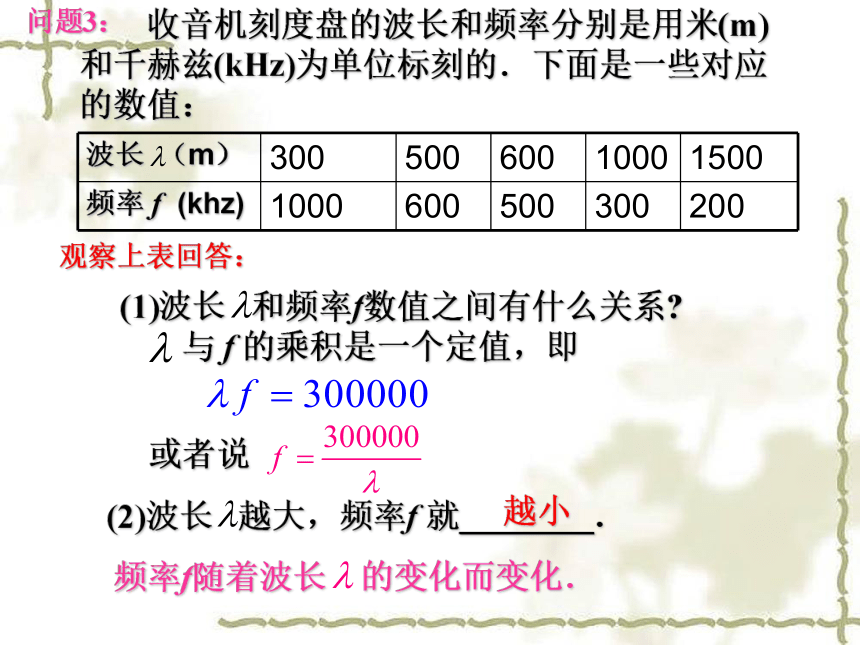
(1)这天的6时、10时和14时的气温分别为多少？任意给出这天中的某一时刻，说出这一时刻的气温．(2)这一天中，最高气温是多少？最低气温是多少？(3)这一天中，什么时段的气温在逐渐升高？什么时段的气温在逐渐降低？ ··温度T随着时间t的变化而变化．问题1： 银行对各种不同的存款方式都规定了相应的利率，下表是2006年8月中国人民银行为“整存整取”的存款方式规定的年利率： 观察上表，说说随着存期x的增长，相应的年利率y是如何变化的． 随着存期x的增长，相应的年利率y也随着增长．年利率y随着存期x的变化而变化．问题2： 收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的．下面是一些对应的数值： 观察上表回答：与 f 的乘积是一个定值，即或者说 (1)波长 和频率f数值之间有什么关系?(2)波长 越大，频率f 就________．越小频率f随着波长 的变化而变化．问题3：问题4：如果用r表示圆的半径，S表示圆的面积，则S与r之间满足下列关系：S=利用这个关系式，试求出半径为1cm、1.5cm、2cm、2.6cm、3.2cm时圆的面积，并将结果填入下表：圆的半径越大，它的面积就越大圆的面积S随着半径r的变化而变化．１、一辆汽车以30千米/时的速度行驶，行驶
的路程s(千米)与行驶的时间t(小时)有怎样的
关系呢？２、圆的面积S与半径r有怎样的关系？S=30tS=лr2 实例引入1、常量与变量的概念：常量：在某一变化过程中，始终保持不变的量．变量：在某一变化过程中，可以取不同数值的量．基本概念2、自变量、函数的概念设在某一变化过程中有两个变量x和y，如果对于x的每一个值，y总有唯一的值与它对应，我们就说x是自变量，y是x的函数．概念整理引例
已知等腰三角形的周长为10，腰长为x，底边长为y，写出y与x的函数关系式，并求出x的取值范围.说明:在用解析式表示函数时，要考虑自变量必须使解析式有意义的取值.灵活运用y与x的函数关系式为：试一试图4-2(2) 当r = 5时， ；
当r = 10 时， .
图4-2(1)用含r 的代数式来表示圆柱的体积V，指出
自变量r 的取值范围.(2)当r = 5 ，10时，V是多少(结果保留π)？求下列函数中自变量x的取值范围：
（1） y＝3x－1 （2） y＝2x2＋7
（3） y= （4） y=(1)因为x取任意实数， 都有意义，所以x的取值范围是任意实数．(2)因为x取任意实数，　　 都有意义，所以x的取值范围是任意实数．(3)因为x+2不等于0时， 才有意义，所以
x的取值范围是:(4)因为x≥2时， 才有意义，所以x的取值范围是x≥2 ．练习引例、如图，等腰直角△ABC的直角边长与正方形MNPQ的边长均为10 cm，AC与MN在同一直线上，开始时A点与M点重合，让△ABC向右运动，最后A点与N点重合．试写出重叠部分面积ycm2与MA长度x cm之间的函数关系式． 当MA＝1 cm时，重叠部分的面积是多少?
解:设重叠部分面积为y cm2，MA长为x cm，
容易求出y与x之间的函数关系式为 : 当x＝1时，y=所以当MA＝1 cm时，重叠部分的面积是 cm2 ．　 y=小结1. 自变量取值范围的确定； 2. 具有实际意义的函数要考虑实际意义．收获知多少？