2.4 一元二次方程根与系数的关系 教案
文档属性
| 名称 | 2.4 一元二次方程根与系数的关系 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 26.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-19 21:13:23 | ||
图片预览

文档简介
2.4
一元二次方程根与系数的关系
教案
教学目标
知识技能:
掌握一元二次方程根和系数的关系,能不解方程求出一元二次方程的两根和与两根积.
能利用一元二次方程根与系数的关系来判断已知两数是否是原方程的根,能灵活解决一些简单的有关一元二次方程的问题.
过程与方法:
经过小组讨论和从特殊到一般的数学认知过程的体会.
教学重点
一元二次方程根与系数的关系.
教学难点
韦达定理的论证
教学过程
一、复习.
1、一元二次方程的一般式?
,
2、一元二次方程有实数根的条件是什么?(
3、>0
,即△>0,△=0,△<0
根的情况如何?
反过来,若方程有两个不相等的实数根,说明△怎么样等?
4、一元二次方程的求根公式.
二、引入.
由求根公式可知,一元二次方程的根由系数、、确定,换句话就是说根与系数有关系,今天我们将进一步来学习并发现一元二次方程的根与系数到底还有没有其他关系.
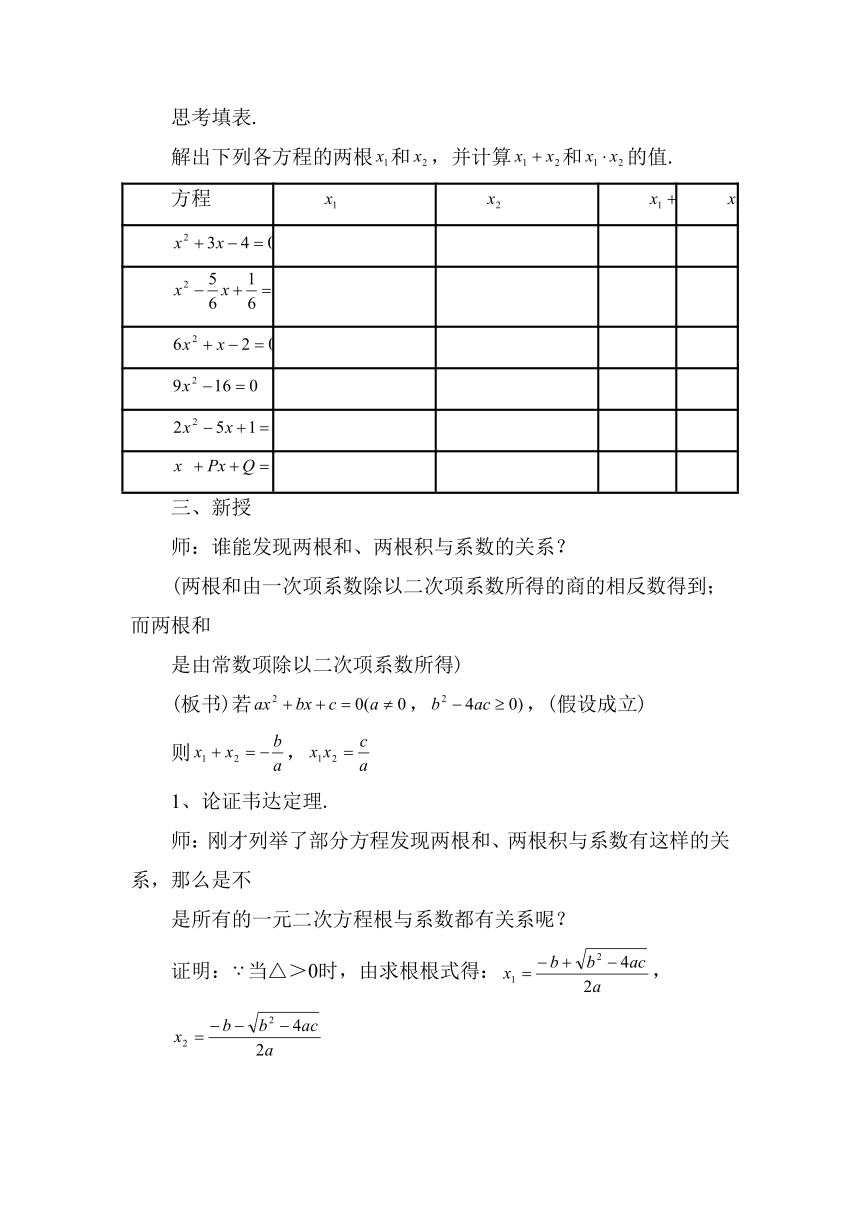
思考填表.
解出下列各方程的两根和,并计算和的值.
方程
三、新授
师:谁能发现两根和、两根积与系数的关系?
(两根和由一次项系数除以二次项系数所得的商的相反数得到;而两根和
是由常数项除以二次项系数所得)
(板书)若,,(假设成立)
则,
1、论证韦达定理.
师:刚才列举了部分方程发现两根和、两根积与系数有这样的关系,那么是不
是所有的一元二次方程根与系数都有关系呢?
证明:当△>0时,由求根根式得:,
∴
当△=0时,
即
师:假设成立,这就是一元二次方程根与系数的关系,也称韦达定理,因为是
法国数学家韦达最先发现的.
2、翻书P47.(让学生划下韦达定理)
3、写出方程的两根和与两根积,并解方程检验其结果.
解:设方程的两根为,.则
检验:由求根公式得
,
课堂小结
今天我们学习了一元二次方程根与系数的关系,刚才通过填空题我们小结了一下,知道这两个关系我们可以用来求两根和、两根积,而且可以验算所求的根是否正确,更重要的是利用韦达定理可以简捷地解决许多有关一元二次方程的问题.
一元二次方程根与系数的关系
教案
教学目标
知识技能:
掌握一元二次方程根和系数的关系,能不解方程求出一元二次方程的两根和与两根积.
能利用一元二次方程根与系数的关系来判断已知两数是否是原方程的根,能灵活解决一些简单的有关一元二次方程的问题.
过程与方法:
经过小组讨论和从特殊到一般的数学认知过程的体会.
教学重点
一元二次方程根与系数的关系.
教学难点
韦达定理的论证
教学过程
一、复习.
1、一元二次方程的一般式?
,
2、一元二次方程有实数根的条件是什么?(
3、>0
,即△>0,△=0,△<0
根的情况如何?
反过来,若方程有两个不相等的实数根,说明△怎么样等?
4、一元二次方程的求根公式.
二、引入.
由求根公式可知,一元二次方程的根由系数、、确定,换句话就是说根与系数有关系,今天我们将进一步来学习并发现一元二次方程的根与系数到底还有没有其他关系.
思考填表.
解出下列各方程的两根和,并计算和的值.
方程
三、新授
师:谁能发现两根和、两根积与系数的关系?
(两根和由一次项系数除以二次项系数所得的商的相反数得到;而两根和
是由常数项除以二次项系数所得)
(板书)若,,(假设成立)
则,
1、论证韦达定理.
师:刚才列举了部分方程发现两根和、两根积与系数有这样的关系,那么是不
是所有的一元二次方程根与系数都有关系呢?
证明:当△>0时,由求根根式得:,
∴
当△=0时,
即
师:假设成立,这就是一元二次方程根与系数的关系,也称韦达定理,因为是
法国数学家韦达最先发现的.
2、翻书P47.(让学生划下韦达定理)
3、写出方程的两根和与两根积,并解方程检验其结果.
解:设方程的两根为,.则
检验:由求根公式得
,
课堂小结
今天我们学习了一元二次方程根与系数的关系,刚才通过填空题我们小结了一下,知道这两个关系我们可以用来求两根和、两根积,而且可以验算所求的根是否正确,更重要的是利用韦达定理可以简捷地解决许多有关一元二次方程的问题.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
