人教A版数学必修一2.1 指数函数 课件 (共29张PPT)
文档属性
| 名称 | 人教A版数学必修一2.1 指数函数 课件 (共29张PPT) | 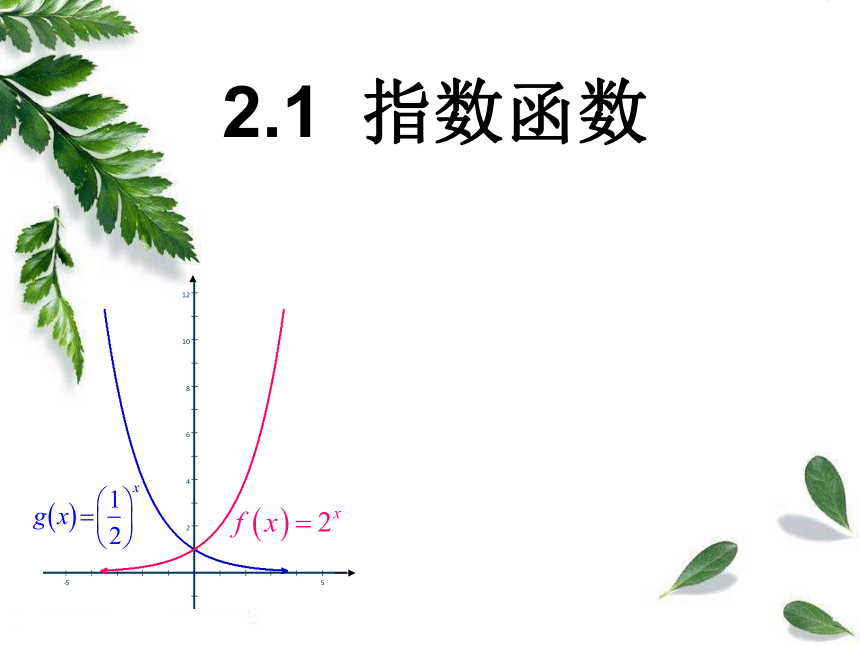 | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-19 14:54:58 | ||
图片预览





文档简介
课件29张PPT。
2.1 指数函数
学习目标1、了解指数函数模型的实际背景;
2、理解指数函数的概念、图像和性质。
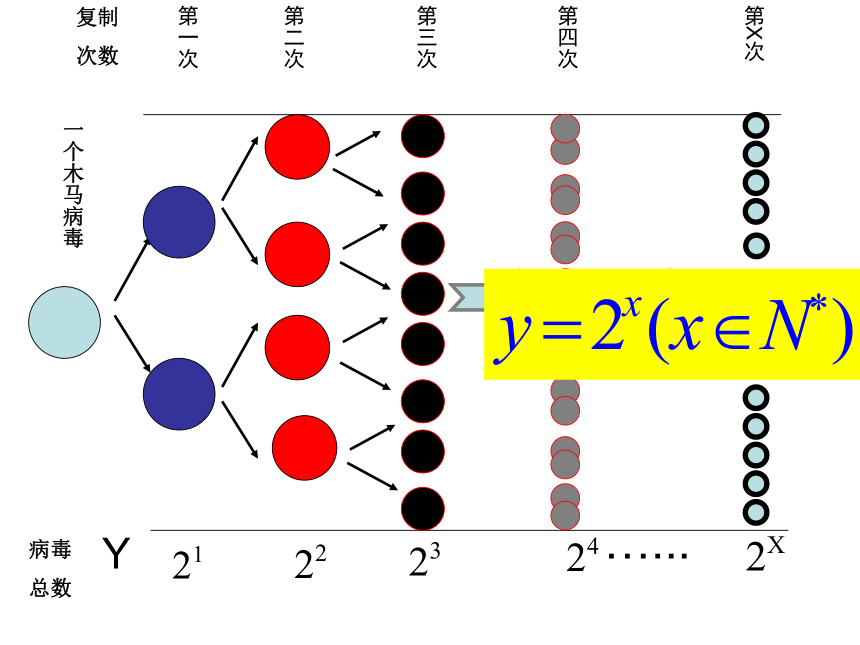
指数函数的性质和应用。 重点难点指数函数的概念和性质。庄子曰:一尺之棰,日取其半,万世不竭。 一尺长的棍子,第一天取掉其一半,第二天取其剩余的一半……,请写出取x次后,木棰的剩留量与y与x的函数关系式。 第1次第2次第3次第4次第X次 情景1“ 木马病毒”被认为是破坏性极强的计算机病毒之一,具有快速自我复制能力,它可以由1个变成2个,2个变成4个……复制x次后,你知道所得病毒个数y与x的函数关系式是什么?情景2复制
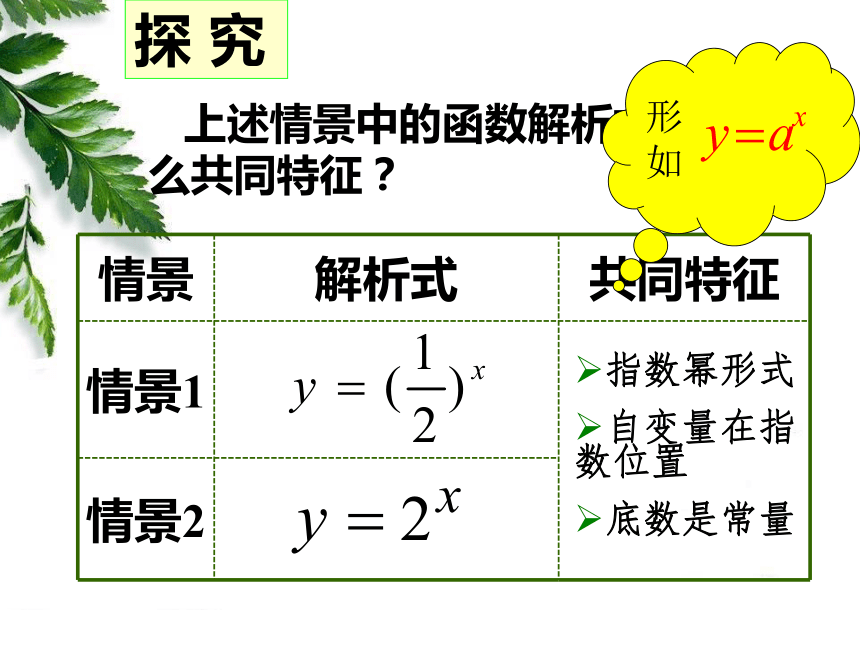
次数第一次第二次第三次第四次…...第X次 上述情景中的函数解析式有什么共同特征?2探 究指数幂形式
自变量在指数位置
底数是常量一、指数函数的定义 一般地,函数
y=a x(a>0 且 a ≠ 1,x ? R )
叫做指数函数.其中 x 是自变量,定义域为 R.解析式的特点:1、系数必须是1;
2、底数必须是大于零且不等于1的常数;
3、x在幂指数上且只能是x.
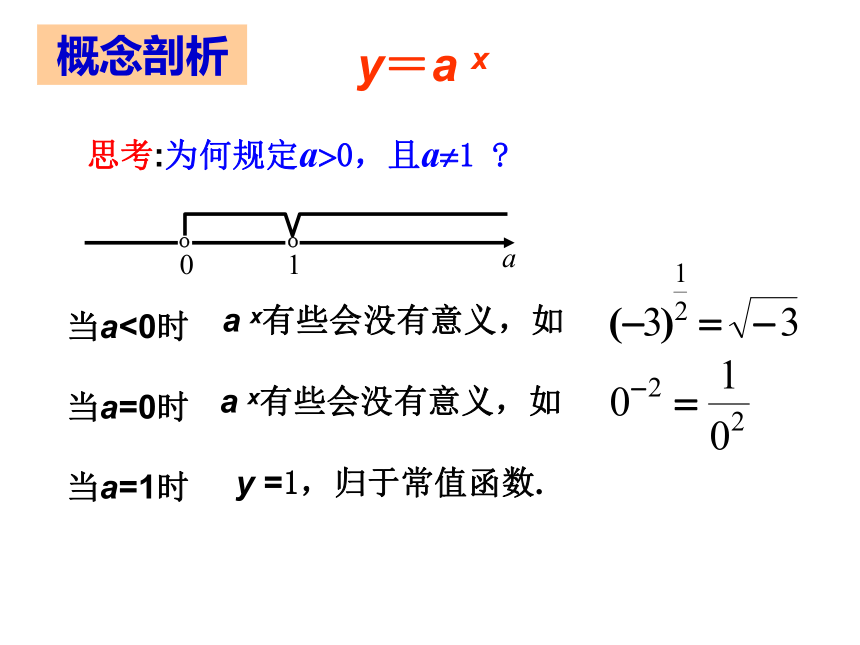
概念剖析y =1,归于常值函数.思考:为何规定a?0,且a?1 ?a x有些会没有意义,如 a x有些会没有意义,如 y=a x当a<0时
当a=0时
当a=1时
练习:指出下列函数哪些是指数函数:(1)y=(-3)x; (2) y=?x ;(3)y=0.7x; (4) y=x3.
(口答)判断下列函数是不是指 数函数,为什么?√√
二、指数函数的性质探究:用描点法画出指数函
数 和 的图象.… 8 4 21…y= 2x… 3 2 10-1-2-3… x.8 7 6 5 4 3 2 1 -3 -2 -1 0 1 2 3… 8 4 21…y= 2x… 3 2 10-1-2-3… xxyy =2x8 7 6 5 4 3 2 1 -3 -2 -1 0 1 2 3… 8 4 21…… 3 2 10-1-2-3… xxyy =2x -3 -2 -1 0 1 2 3yy =2x8 7 6 5 4 3 2 1 x(1)图象都位于x轴上方(2)图象都过点(0,1)(3) y=2x的图象从左到右上升
的图象从左到右下降(0,1)观察以下图形:你有什么奇妙的发现呢? a > 1 0R( 0 , + ∞)过定点 ( 0 , 1 ) 在R上是增函数在R上是减函数 (1)定义域 (2)值域 (3)定点 (4)单调性a > 10 < a < 1指数函数的图象和性质 指函图象半个八,
大一撇来小一捺,???????
图象必过(0,1)点,?
X轴上方为指家.? 例1 用指数函数的性质,判断下列各
函数的单调性:解:(1)因为3>1,所以 在R上是增函数.例题讲解 所以 y=( ) x 在R上是减函数.(2)因为0< <1,
知识接力
活动规则:每组分别仿照例1给下一组
出题,并指定相应学生回答。回答对的学生可继续出题依次类推。
要求:声音洪亮,使对方听清。
解:(1)因为3>1,所以 在R上是增函数.例2 比较下列各题中两个值的大小1.72.5与1.73
解:(1) 考虑指数函数 y=1.7x,它是增函数.∵2.5<3 ∴1.72.5<1.73.例题讲解例2 比较下列各题中两个值的大小 :1.72.5与1.73
解:(1) 考虑指数函数 y=1.7x它是增函数.∵2.5<3
∴1.72.5<1.73例题讲解(2) 1.2与 5解:(2)考虑指数函数它是 .∵例题讲解练习:比较100.2与1的大小.y= x,减函数1.2< 5∴ 课堂练习:用“>”或“<”填空:>><指数函数一、定义: 函数 y = a x (a>0,且a≠1)
叫做指数函数,其中x是自变量.
二、性质:小结 指函图象半个八,
大一撇来小一捺,???????
图象必过(0,1)点,?
X轴上方为指家.? 知识延展每人拿出一张纸,进行对折,你能折几次? “帮你发财”理财公司想和你签约,
从今天开始每天给你10万元,而你承担如下任务:
第一天给公司1元,
第二天给公司2元,
第三天给公司4元,
第四天给公司8元,依次下去…那么,
要和你签定15天的合同,你同意吗?
公司要和你签定30天的合同,你能签这个合同吗?
15天公司给你:150万 你给公司:32767元
30天公司给你:300万 你给公司:1073741824元学以致用
新版借钱又要钱?借多少?这样吧,从今天开始在一个月中,我每天都借你10万元,而你从今天开始,第一天还我1元,第二天2元,第三天4元,第四天8元,.......以后知道怎么还了吗?黄老板,能借点钱吗?10万可以吗? 哦,我每天还的钱是前一天的2倍是吧,那我需要很久才能还完你啊? 不,你只要还我三十天就可以了,剩下的就不要了。太好啦。作 业 2.课下通过调查和上网搜索生活中与指数函数相关的问题,并用学过知识加以分析应用,用数学去装扮自己的生活!
(这是一个长期作业,可以小组合作完成) 1. p81练习 第1题、第2题希望今天的学习
能让你有所收获!
同学们,再见!谢谢光临指导
2.1 指数函数
学习目标1、了解指数函数模型的实际背景;
2、理解指数函数的概念、图像和性质。
指数函数的性质和应用。 重点难点指数函数的概念和性质。庄子曰:一尺之棰,日取其半,万世不竭。 一尺长的棍子,第一天取掉其一半,第二天取其剩余的一半……,请写出取x次后,木棰的剩留量与y与x的函数关系式。 第1次第2次第3次第4次第X次 情景1“ 木马病毒”被认为是破坏性极强的计算机病毒之一,具有快速自我复制能力,它可以由1个变成2个,2个变成4个……复制x次后,你知道所得病毒个数y与x的函数关系式是什么?情景2复制
次数第一次第二次第三次第四次…...第X次 上述情景中的函数解析式有什么共同特征?2探 究指数幂形式
自变量在指数位置
底数是常量一、指数函数的定义 一般地,函数
y=a x(a>0 且 a ≠ 1,x ? R )
叫做指数函数.其中 x 是自变量,定义域为 R.解析式的特点:1、系数必须是1;
2、底数必须是大于零且不等于1的常数;
3、x在幂指数上且只能是x.
概念剖析y =1,归于常值函数.思考:为何规定a?0,且a?1 ?a x有些会没有意义,如 a x有些会没有意义,如 y=a x当a<0时
当a=0时
当a=1时
练习:指出下列函数哪些是指数函数:(1)y=(-3)x; (2) y=?x ;(3)y=0.7x; (4) y=x3.
(口答)判断下列函数是不是指 数函数,为什么?√√
二、指数函数的性质探究:用描点法画出指数函
数 和 的图象.… 8 4 21…y= 2x… 3 2 10-1-2-3… x.8 7 6 5 4 3 2 1 -3 -2 -1 0 1 2 3… 8 4 21…y= 2x… 3 2 10-1-2-3… xxyy =2x8 7 6 5 4 3 2 1 -3 -2 -1 0 1 2 3… 8 4 21…… 3 2 10-1-2-3… xxyy =2x -3 -2 -1 0 1 2 3yy =2x8 7 6 5 4 3 2 1 x(1)图象都位于x轴上方(2)图象都过点(0,1)(3) y=2x的图象从左到右上升
的图象从左到右下降(0,1)观察以下图形:你有什么奇妙的发现呢? a > 1 0
大一撇来小一捺,???????
图象必过(0,1)点,?
X轴上方为指家.? 例1 用指数函数的性质,判断下列各
函数的单调性:解:(1)因为3>1,所以 在R上是增函数.例题讲解 所以 y=( ) x 在R上是减函数.(2)因为0< <1,
知识接力
活动规则:每组分别仿照例1给下一组
出题,并指定相应学生回答。回答对的学生可继续出题依次类推。
要求:声音洪亮,使对方听清。
解:(1)因为3>1,所以 在R上是增函数.例2 比较下列各题中两个值的大小1.72.5与1.73
解:(1) 考虑指数函数 y=1.7x,它是增函数.∵2.5<3 ∴1.72.5<1.73.例题讲解例2 比较下列各题中两个值的大小 :1.72.5与1.73
解:(1) 考虑指数函数 y=1.7x它是增函数.∵2.5<3
∴1.72.5<1.73例题讲解(2) 1.2与 5解:(2)考虑指数函数它是 .∵例题讲解练习:比较100.2与1的大小.y= x,减函数1.2< 5∴ 课堂练习:用“>”或“<”填空:>><指数函数一、定义: 函数 y = a x (a>0,且a≠1)
叫做指数函数,其中x是自变量.
二、性质:小结 指函图象半个八,
大一撇来小一捺,???????
图象必过(0,1)点,?
X轴上方为指家.? 知识延展每人拿出一张纸,进行对折,你能折几次? “帮你发财”理财公司想和你签约,
从今天开始每天给你10万元,而你承担如下任务:
第一天给公司1元,
第二天给公司2元,
第三天给公司4元,
第四天给公司8元,依次下去…那么,
要和你签定15天的合同,你同意吗?
公司要和你签定30天的合同,你能签这个合同吗?
15天公司给你:150万 你给公司:32767元
30天公司给你:300万 你给公司:1073741824元学以致用
新版借钱又要钱?借多少?这样吧,从今天开始在一个月中,我每天都借你10万元,而你从今天开始,第一天还我1元,第二天2元,第三天4元,第四天8元,.......以后知道怎么还了吗?黄老板,能借点钱吗?10万可以吗? 哦,我每天还的钱是前一天的2倍是吧,那我需要很久才能还完你啊? 不,你只要还我三十天就可以了,剩下的就不要了。太好啦。作 业 2.课下通过调查和上网搜索生活中与指数函数相关的问题,并用学过知识加以分析应用,用数学去装扮自己的生活!
(这是一个长期作业,可以小组合作完成) 1. p81练习 第1题、第2题希望今天的学习
能让你有所收获!
同学们,再见!谢谢光临指导
