冲刺2010中考复习(6)一元一次不等式(组)
文档属性
| 名称 | 冲刺2010中考复习(6)一元一次不等式(组) |

|
|
| 格式 | zip | ||
| 文件大小 | 439.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-30 00:00:00 | ||
图片预览



文档简介
本系列资料系2010中考第一轮复习精品资料,每一篇内容分为三个版块:内容解读、考点剖析、真题训练,精选近几年各地中考题,适合全层次初三学生系统复习初中数学知识。
冲刺2010第一轮复习(6)
第六讲 一元一次不等式(组)
内容解读
中考对于不等式的要求主要包括不等式的性质,一元一次不等式(组)的解法和应用。其中一元一次不等式(组)及其解法是中考的考查热点之一,近年的中考还注重考查学生运用一元一次不等式(组)的知识分析和解决问题的能力。
考点剖析
1、不等式的性质
例1:(2009临沂)若,则下列式子错误的是( )
A. B.
C. D.
解答:B
例2、(2009佛山)据佛山日报报道,2009年6月1日佛山市最高气温是33℃,最低气温是24℃,则当天佛山市气温(℃)的变化范围是( )
A. B. C. D.
解答:D
2、不等式的解集
例3:(2008白银)把不等式组的解集表示在数轴上,正确的为图中的( )
A. B. C. D.
解答:B
3、不等式(组)的解法
例4:(2009荆州)解不等式:
解答:
例5:(2008青海)解不等式组并求出所有整数解的和.
解答:解不等式①,得,
解不等式②,得.
原不等式组的解集是.
则原不等式组的整数解是.
所有整数解的和是:.
4、不等式(组)的应用
例6:(2008襄樊)“六一”儿童节前夕,某消防队官兵了解到汶川地震灾区一帐篷小学的小朋友喜欢奥运福娃,就特意购买了一些送给这个小学的小朋友作为节日礼物.如果每班分10套,那么余5套;如果前面的班级每个班分13套,那么最后一个班级虽然分有福娃,但不足4套.问:该小学有多少个班级?奥运福娃共有多少套?
解答:解:设该小学有个班,则奥运福娃共有套.
由题意,得
解之,得.
只能取整数,,此时.
答:该小学有5个班级,共有奥运福娃55套.
真题训练
1、(2009柳州)若,则下列各式中一定成立的是( )
A. B.
C. D.
2、(2008永州)如图,a、b、c分别表示苹果、梨、桃子的质量.同类水果质量相等,则下列关系正确的是( )
A.a>c>b B.b>a>c C.a>b>c D.c>a>b
3、(2008烟台)关于不等式的解集如图所示,的值是( )
A、0 B、2 C、-2 D、-4
4、(2008黄石)若不等式组有实数解,则实数的取值范围是( )
A. B. C. D.
5、(2009恩施)如果一元一次不等式组的解集为.则的取值范围是( )
A. B. C. D.
6、(2007咸宁)不等式组的整数解是_________________.
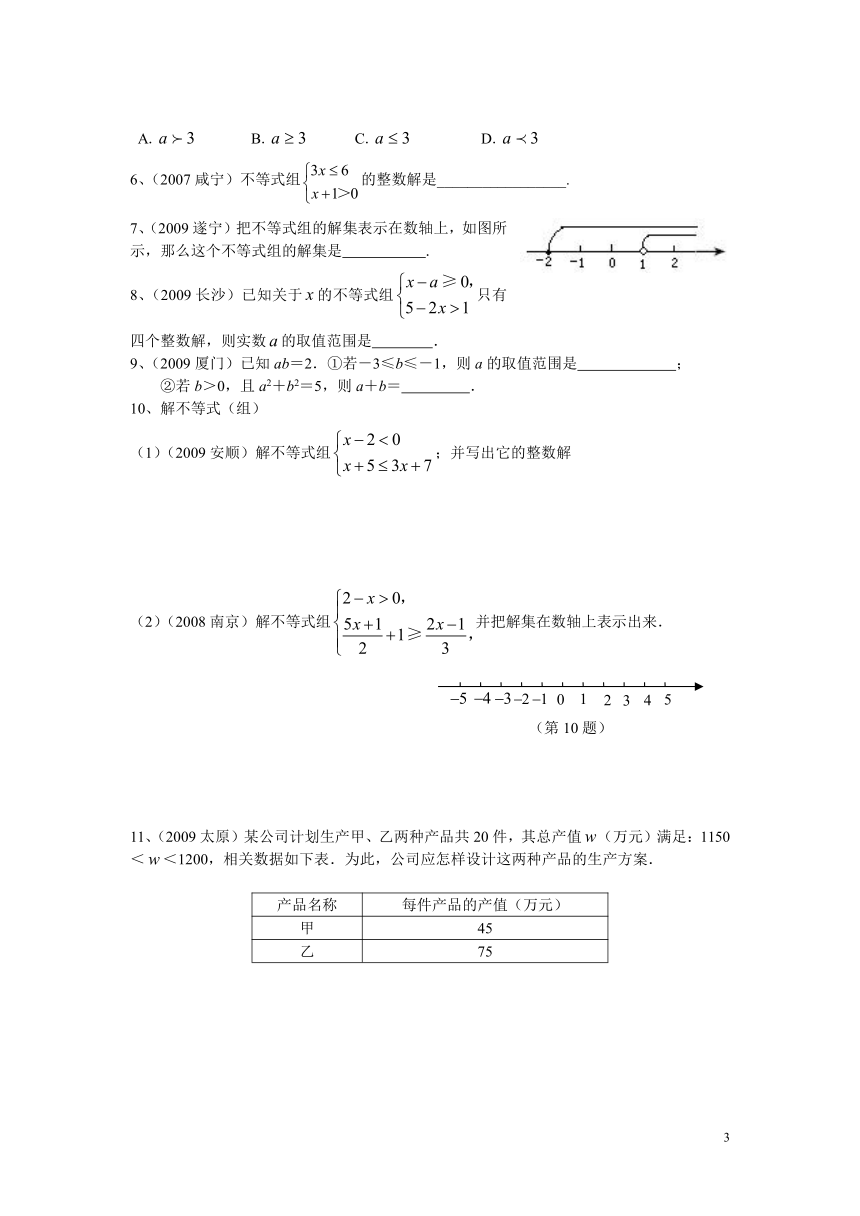
7、(2009遂宁)把不等式组的解集表示在数轴上,如图所示,那么这个不等式组的解集是 .
8、(2009长沙)已知关于的不等式组只有四个整数解,则实数的取值范围是 .
9、(2009厦门)已知ab=2.①若-3≤b≤-1,则a的取值范围是 ;
②若b>0,且a2+b2=5,则a+b= .
10、解不等式(组)
(1)(2009安顺)解不等式组;并写出它的整数解
(2)(2008南京)解不等式组并把解集在数轴上表示出来.
11、(2009太原)某公司计划生产甲、乙两种产品共20件,其总产值(万元)满足:1150<<1200,相关数据如下表.为此,公司应怎样设计这两种产品的生产方案.
产品名称 每件产品的产值(万元)
甲 45
乙 75
12、(2009威海)响应“家电下乡”的惠农政策,某商场决定从厂家购进甲、乙、丙三种不同型号的电冰箱80台,其中甲种电冰箱的台数是乙种电冰箱台数的2倍,购买三种电冰箱的总金额不超过132 000元.已知甲、乙、丙三种电冰箱的出厂价格分别为:1 200元/台、1 600元/台、2 000元/台.
(1) 至少购进乙种电冰箱多少台?
(1) 若要求甲种电冰箱的台数不超过丙种电冰箱的台数,则有哪些购买方案?
13、(2009遂宁)某校原有600张旧课桌急需维修,经过A、B、C三个工程队的竞标得知,A、B的工作效率相同,且都为C队的2倍,若由一个工程队单独完成,C队比A 队要多用10天.学校决定由三个工程队一齐施工,要求至多6天完成维修任务.三个工程队都按原来的工作效率施工2天时,学校又清理出需要维修的课桌360张,为了不超过6天时限,工程队决定从第3天开始,各自都提高工作效率,A、B队提高的工作效率仍然都是C队提高的2倍.这样他们至少还需要3天才能成整个维修任务.
⑴求工程队A原来平均每天维修课桌的张数;
⑵求工程队A提高工作效率后平均每天多维修课桌张数的取值范围.
14、(2008无锡)在“512大地震”灾民安置工作中,某企业接到一批生产甲种板材24000和乙种板材12000的任务.
(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30或乙种板材20.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间型板房和一间型板房所需板材及能安置的人数如下表所示:
板房型号 甲种板材 乙种板材 安置人数
型板房 54 26 5
型板房 78 41 8
问:这400间板房最多能安置多少灾民?
15、(2009温州)某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所彖的竖式与横式两种长方体形状的无盖纸盒.
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共l00个,设做竖式纸盒x个.①根据题意,完成以下表格:
竖式纸盒(个) 横式纸盒(个)
x
正方形纸板(张) 2(100-x)
长方形纸板(张) 4x
②按两种纸盒的生产个数来分,有哪几种生产方案
(2)若有正方形纸板162张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完.已知290参考答案
真题训练
1、A 2、C 3、A 4、A 5、C
6、0,1,2
7、x>1
8、
9、(1) -2≤a≤- ;(2) 3 .
10、(1)解:解①得 解②得
∴ ∴所求不等式组的整数解为:-1. 0. 1 .
(2)解:解不等式①,得.
解不等式②,得.
所以,不等式组的解集是.
不等式组的解集在数轴上表示如下:
11、解:设计划生产甲产品件,则生产乙产品件,
根据题意,得 ( http: / / www. / )
解得.
为整数,∴此时,( 件).
答:公司应安排生产甲产品11件,乙产品9件.
12、解:(1)设购买乙种电冰箱台,则购买甲种电冰箱台,
丙种电冰箱台,根据题意,列不等式:
.
解这个不等式,得.
至少购进乙种电冰箱14台.
(2)根据题意,得.
解这个不等式,得.
由(1)知.
.
又为正整数,
.
所以,有三种购买方案:
方案一:甲种电冰箱为28台,乙种电冰箱为14台,丙种电冰箱为38台;
方案二:甲种电冰箱为30台,乙种电冰箱为15台,丙种电冰箱为35台;
方案三:甲种电冰箱为32台,乙种电冰箱为16台,丙种电冰箱为32台.
13、⑴设C队原来平均每天维修课桌x张,
根据题意得:
解这个方程得:x=30
经检验x=30是原方程的根且符合题意,2x=60
答:A队原来平均每天维修课桌60张.
⑵设C队提高工效后平均每天多维修课桌x张,施工2天时,已维修(60+60+30)×2=300(张),从第3天起还需维修的张数应为(300+360)=600(张)
根据题意得:
3(2x+2x+x+150)≤660≤4(2x+2x+x+150)
解这个不等式组得::3≤x≤14
∴6≤2x≤28
答:A队提高工效后平均每天多维修的课桌张数的取值范围是:6≤2x≤28
14、解:(1)设安排人生产甲种板材,
则生产乙种板材的人数为人.
由题意,得,
解得:.经检验,是方程的根,且符合题意.
答:应安排80人生产甲种板材,60人生产乙种板材.
(2)设建造型板房间,则建造型板房为间,
由题意有:
解得.
又,.
这400间板房可安置灾民.
当时,取得最大值2300名.
答:这400间板房最多能安置灾民2300名.
15、
(第10题)
PAGE
6
冲刺2010第一轮复习(6)
第六讲 一元一次不等式(组)
内容解读
中考对于不等式的要求主要包括不等式的性质,一元一次不等式(组)的解法和应用。其中一元一次不等式(组)及其解法是中考的考查热点之一,近年的中考还注重考查学生运用一元一次不等式(组)的知识分析和解决问题的能力。
考点剖析
1、不等式的性质
例1:(2009临沂)若,则下列式子错误的是( )
A. B.
C. D.
解答:B
例2、(2009佛山)据佛山日报报道,2009年6月1日佛山市最高气温是33℃,最低气温是24℃,则当天佛山市气温(℃)的变化范围是( )
A. B. C. D.
解答:D
2、不等式的解集
例3:(2008白银)把不等式组的解集表示在数轴上,正确的为图中的( )
A. B. C. D.
解答:B
3、不等式(组)的解法
例4:(2009荆州)解不等式:
解答:
例5:(2008青海)解不等式组并求出所有整数解的和.
解答:解不等式①,得,
解不等式②,得.
原不等式组的解集是.
则原不等式组的整数解是.
所有整数解的和是:.
4、不等式(组)的应用
例6:(2008襄樊)“六一”儿童节前夕,某消防队官兵了解到汶川地震灾区一帐篷小学的小朋友喜欢奥运福娃,就特意购买了一些送给这个小学的小朋友作为节日礼物.如果每班分10套,那么余5套;如果前面的班级每个班分13套,那么最后一个班级虽然分有福娃,但不足4套.问:该小学有多少个班级?奥运福娃共有多少套?
解答:解:设该小学有个班,则奥运福娃共有套.
由题意,得
解之,得.
只能取整数,,此时.
答:该小学有5个班级,共有奥运福娃55套.
真题训练
1、(2009柳州)若,则下列各式中一定成立的是( )
A. B.
C. D.
2、(2008永州)如图,a、b、c分别表示苹果、梨、桃子的质量.同类水果质量相等,则下列关系正确的是( )
A.a>c>b B.b>a>c C.a>b>c D.c>a>b
3、(2008烟台)关于不等式的解集如图所示,的值是( )
A、0 B、2 C、-2 D、-4
4、(2008黄石)若不等式组有实数解,则实数的取值范围是( )
A. B. C. D.
5、(2009恩施)如果一元一次不等式组的解集为.则的取值范围是( )
A. B. C. D.
6、(2007咸宁)不等式组的整数解是_________________.
7、(2009遂宁)把不等式组的解集表示在数轴上,如图所示,那么这个不等式组的解集是 .
8、(2009长沙)已知关于的不等式组只有四个整数解,则实数的取值范围是 .
9、(2009厦门)已知ab=2.①若-3≤b≤-1,则a的取值范围是 ;
②若b>0,且a2+b2=5,则a+b= .
10、解不等式(组)
(1)(2009安顺)解不等式组;并写出它的整数解
(2)(2008南京)解不等式组并把解集在数轴上表示出来.
11、(2009太原)某公司计划生产甲、乙两种产品共20件,其总产值(万元)满足:1150<<1200,相关数据如下表.为此,公司应怎样设计这两种产品的生产方案.
产品名称 每件产品的产值(万元)
甲 45
乙 75
12、(2009威海)响应“家电下乡”的惠农政策,某商场决定从厂家购进甲、乙、丙三种不同型号的电冰箱80台,其中甲种电冰箱的台数是乙种电冰箱台数的2倍,购买三种电冰箱的总金额不超过132 000元.已知甲、乙、丙三种电冰箱的出厂价格分别为:1 200元/台、1 600元/台、2 000元/台.
(1) 至少购进乙种电冰箱多少台?
(1) 若要求甲种电冰箱的台数不超过丙种电冰箱的台数,则有哪些购买方案?
13、(2009遂宁)某校原有600张旧课桌急需维修,经过A、B、C三个工程队的竞标得知,A、B的工作效率相同,且都为C队的2倍,若由一个工程队单独完成,C队比A 队要多用10天.学校决定由三个工程队一齐施工,要求至多6天完成维修任务.三个工程队都按原来的工作效率施工2天时,学校又清理出需要维修的课桌360张,为了不超过6天时限,工程队决定从第3天开始,各自都提高工作效率,A、B队提高的工作效率仍然都是C队提高的2倍.这样他们至少还需要3天才能成整个维修任务.
⑴求工程队A原来平均每天维修课桌的张数;
⑵求工程队A提高工作效率后平均每天多维修课桌张数的取值范围.
14、(2008无锡)在“512大地震”灾民安置工作中,某企业接到一批生产甲种板材24000和乙种板材12000的任务.
(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30或乙种板材20.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间型板房和一间型板房所需板材及能安置的人数如下表所示:
板房型号 甲种板材 乙种板材 安置人数
型板房 54 26 5
型板房 78 41 8
问:这400间板房最多能安置多少灾民?
15、(2009温州)某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所彖的竖式与横式两种长方体形状的无盖纸盒.
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共l00个,设做竖式纸盒x个.①根据题意,完成以下表格:
竖式纸盒(个) 横式纸盒(个)
x
正方形纸板(张) 2(100-x)
长方形纸板(张) 4x
②按两种纸盒的生产个数来分,有哪几种生产方案
(2)若有正方形纸板162张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完.已知290
真题训练
1、A 2、C 3、A 4、A 5、C
6、0,1,2
7、x>1
8、
9、(1) -2≤a≤- ;(2) 3 .
10、(1)解:解①得 解②得
∴ ∴所求不等式组的整数解为:-1. 0. 1 .
(2)解:解不等式①,得.
解不等式②,得.
所以,不等式组的解集是.
不等式组的解集在数轴上表示如下:
11、解:设计划生产甲产品件,则生产乙产品件,
根据题意,得 ( http: / / www. / )
解得.
为整数,∴此时,( 件).
答:公司应安排生产甲产品11件,乙产品9件.
12、解:(1)设购买乙种电冰箱台,则购买甲种电冰箱台,
丙种电冰箱台,根据题意,列不等式:
.
解这个不等式,得.
至少购进乙种电冰箱14台.
(2)根据题意,得.
解这个不等式,得.
由(1)知.
.
又为正整数,
.
所以,有三种购买方案:
方案一:甲种电冰箱为28台,乙种电冰箱为14台,丙种电冰箱为38台;
方案二:甲种电冰箱为30台,乙种电冰箱为15台,丙种电冰箱为35台;
方案三:甲种电冰箱为32台,乙种电冰箱为16台,丙种电冰箱为32台.
13、⑴设C队原来平均每天维修课桌x张,
根据题意得:
解这个方程得:x=30
经检验x=30是原方程的根且符合题意,2x=60
答:A队原来平均每天维修课桌60张.
⑵设C队提高工效后平均每天多维修课桌x张,施工2天时,已维修(60+60+30)×2=300(张),从第3天起还需维修的张数应为(300+360)=600(张)
根据题意得:
3(2x+2x+x+150)≤660≤4(2x+2x+x+150)
解这个不等式组得::3≤x≤14
∴6≤2x≤28
答:A队提高工效后平均每天多维修的课桌张数的取值范围是:6≤2x≤28
14、解:(1)设安排人生产甲种板材,
则生产乙种板材的人数为人.
由题意,得,
解得:.经检验,是方程的根,且符合题意.
答:应安排80人生产甲种板材,60人生产乙种板材.
(2)设建造型板房间,则建造型板房为间,
由题意有:
解得.
又,.
这400间板房可安置灾民.
当时,取得最大值2300名.
答:这400间板房最多能安置灾民2300名.
15、
(第10题)
PAGE
6
同课章节目录
