冲刺2010中考复习(8)反比例函数
图片预览


文档简介
本系列资料系2010中考复习精品资料,每一篇内容分为三个版块:内容解读、考点剖析、真题训练,精选近几年各地中考题,适合全层次初三学生系统复习初中数学知识。
冲刺2010中考复习(8)
第八讲 反比例函数
内容解读
反比例函数也是中考重点考查的内容之一,它要求考生能结合具体情境体会反比例函数的意义,根据已知条件确定反比例函数的关系式;会画反比例函数的图象,并能根据图象和关系式探索其性质;能用反比例函数解决实际问题。
考点剖析
1、反比例函数的概念
例1:(2009柳州)反比例函数 的图象经过点(2,1),则的值是 .
解答:1
2、反比例函数的图象和性质
例2:(2008常州)若反比例函数的图象在其每个象限内,y随x的增大而减小,则k的值可以是( )
A.-1 B.3 C.0 D.-3
解答:B
例3:(2008新疆)在函数的图象上有三个点的坐标分别为(1,)、(,)、(,),函数值y1、y2、y3的大小关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y2<y1<y3 D.y3<y1<y2
解答:D
3、反比例函数的关系式
例4:(2008宁波)如图,正方形的边长为2,反比例函数过点,
则的值是( )
A. B. C. D.
解答:D
例5:(2009天津)已知图中的曲线是反比例函数(为常数)图象的一支.
(Ⅰ) 这个反比例函数图象的另一支在第几象限?常数的取值范围是什么?
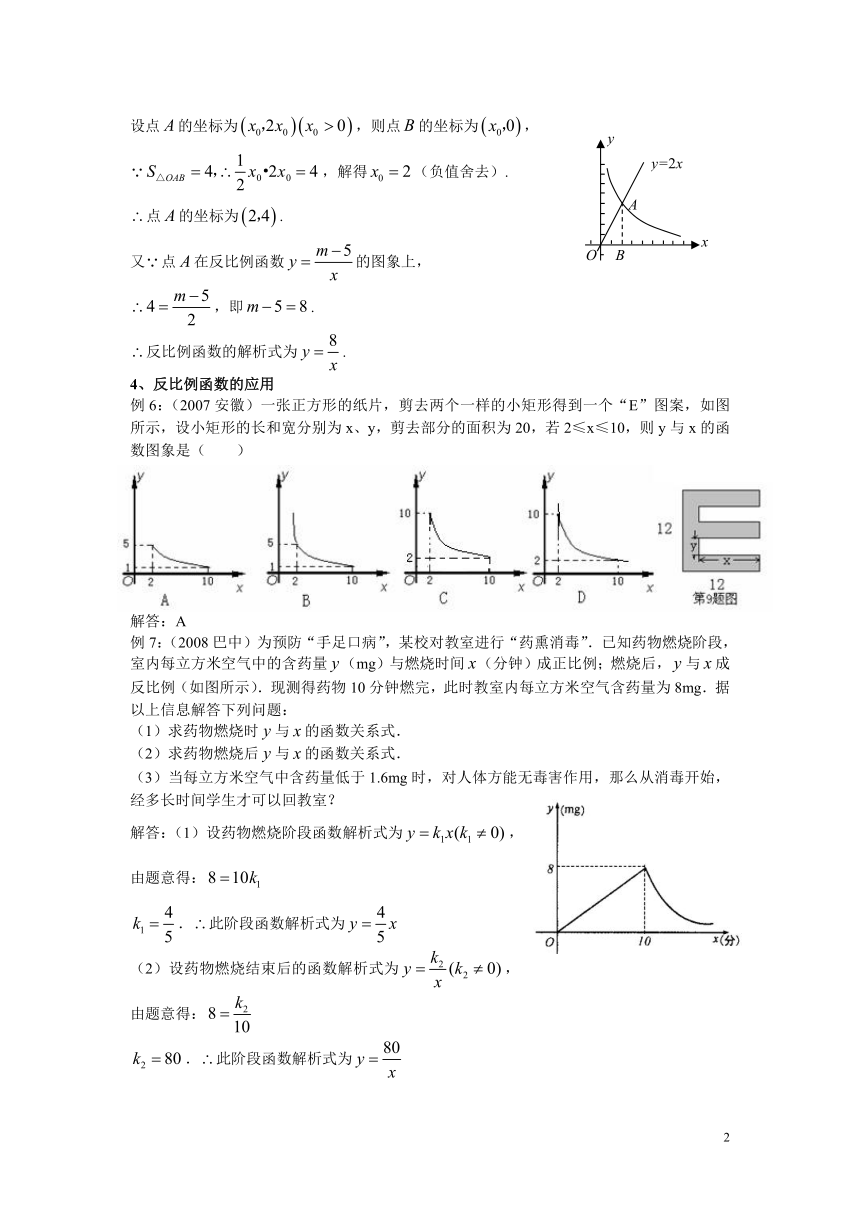
(Ⅱ)若该函数的图象与正比例函数的图象在第一象内限的交点为,过点作轴的垂线,垂足为,当的面积为4时,求点的坐标及反比例函数的解析式.
解答:(Ⅰ)这个反比例函数图象的另一支在第三象限.
因为这个反比例函数的图象分布在第一、第三象限,
所以,解得.
(Ⅱ)如图,由第一象限内的点在正比例函数的图象上,
设点的坐标为,则点的坐标为,
,解得(负值舍去).
点的坐标为.
又点在反比例函数的图象上,
,即.
反比例函数的解析式为.
4、反比例函数的应用
例6:(2007安徽)一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为x、y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( )
解答:A
例7:(2008巴中)为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量(mg)与燃烧时间(分钟)成正比例;燃烧后,与成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
(1)求药物燃烧时与的函数关系式.
(2)求药物燃烧后与的函数关系式.
(3)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室?
解答:(1)设药物燃烧阶段函数解析式为,由题意得:
.此阶段函数解析式为
(2)设药物燃烧结束后的函数解析式为,由题意得:
.此阶段函数解析式为
(3)当时,得
从消毒开始经过50分钟后学生才可回教室.
真题训练
1、(2007南昌)对于反比例函数,下列说法不正确的是( )
A.点在它的图象上 B.它的图象在第一、三象限
C.当时,随的增大而增大 D.当时,随的增大而减小
2、(2009青岛)一块蓄电池的电压为定值,使用此蓄电池为电源时,电流(A)与电阻(Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过10A,那么此用电器的可变电阻应( )
A.不小于4.8Ω B.不大于4.8Ω C.不小于14Ω D.不大于14Ω
3、(2009泰安)如图,双曲线经过矩形QABC的边BC的中点E,交AB于点D。若梯形ODBC的面积为3,则双曲线的解析式为( )
A. B. C. D.
4、(2007孝感)在反比例函数图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k>3 B.k>0 C.k<3 D. k<0
5、(2008济南)如图:等腰直角三角形ABC位于第一象限,
AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,
且两条直角边AB、AC分别平行于x轴、y轴,若双曲线
(k≠0)与有交点,则k的取值范围是( )
A. B. C. D.
6、(2009铁岭)如图所示,反比例函数与正比例函数的图象的一个交点坐标是,若,则的取值范围在数轴上表示为( )
7、(2008河北)点在反比例函数的图象上,则 .
8、(2009山西)若反比例函数的表达式为,则当时,的取值范围是 .
9、(2009佳木斯)反比例函数的图象在每个象限内,随的增大而增大,则的值可以是 .(写出一个符合条件的实数即可)
10、(2008兰州)如图,已知双曲线()经过
矩形的边的中点,且四边形的
面积为2,则 .
11、(2009温州)如图,在平面直角坐标系中,直线AB与Y轴和X轴分别交于点A、点8,与反比例函数y一罟在第一象限的图象交于点c(1,6)、点D(3,x).过点C作CE上y轴于E,过点D作DF上X轴于F.
(1)求m,n的值;
(2)求直线AB的函数解析式;
(3)求证:△AEC∽△DFB.
12、(2009兰州)如图,已知 HYPERLINK "http://www." EMBED Equation.DSMT4 ,是一次函数的图象和反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线与轴的交点的坐标及△的面积;
(3)求方程的解(请直接写出答案);
(4)求不等式的解集(请直接写出答案).
13、(2009河池)为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量(毫克)与时间(分钟)成正比例;药物释放完毕后,与成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,与之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
14、(2009舟山)水产公司有一种海产品共2 104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:
第1天 第2天 第3天 第4天 第5天 第6天 第7天 第8天
售价x(元/千克) 400 250 240 200 150 125 120
销售量y(千克) 30 40 48 60 80 96 100
观察表中数据,发现可以用反比例函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系.
(1) 写出这个反比例函数的解析式,并补全表格;
(2) 在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
(3) 在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?
参考答案
真题训练
题号 1 2 3 4 5 6
答案 C A B A C D
7、2
8、
9、(符合题意即可)
10、2
11、
12、解:(1)在函数的图象上
.
反比例函数的解析式为:.
点在函数的图象上
经过,,
解之得
一次函数的解析式为:
(2)是直线与轴的交点
当时,
点
(3)
(4)
13、解:(1)药物释放过程中与的函数关系式为
(0≤≤12)
药物释放完毕后与的函数关系式为(≥12)
(2) 解之,得 (分钟)(小时)
答: 从药物释放开始,至少需要经过4小时后,学生才能进入教室.
14、解:(1) 函数解析式为.
填表如下:
第1天 第2天 第3天 第4天 第5天 第6天 第7天 第8天
售价x(元/千克) 400 300 250 240 200 150 125 120
销售量y(千克) 30 40 48 50 60 80 96 100
(2) 2 104-(30+40+48+50+60+80+96+100)=1 600,
即8天试销后,余下的海产品还有1 600千克.
当x=150时,=80.
1 600÷80=20,所以余下的这些海产品预计再用20天可以全部售出.
(3) 1 600-80×15=400,400÷2=200,
即如果正好用2天售完,那么每天需要售出200千克.
当y=200时, ( http: / / www. / )=60.
所以新确定的价格最高不超过60元/千克才能完成销售任务.
C
E
B
A
F
O
x
y
(分钟)
12
x
y=2x
A
B
O
y
x
O
y
D.
0
2
1
C.
0
2
1
B.
0
2
1
0
2
A.
1
第6题图
8
I/A
R/Ω
O
6
O
x
y1
y2
第5题图
C
B
A
O
x
1
y
1
2
2
1
y
(毫克)
9
O
B
A
O
C
y
x
PAGE
7
冲刺2010中考复习(8)
第八讲 反比例函数
内容解读
反比例函数也是中考重点考查的内容之一,它要求考生能结合具体情境体会反比例函数的意义,根据已知条件确定反比例函数的关系式;会画反比例函数的图象,并能根据图象和关系式探索其性质;能用反比例函数解决实际问题。
考点剖析
1、反比例函数的概念
例1:(2009柳州)反比例函数 的图象经过点(2,1),则的值是 .
解答:1
2、反比例函数的图象和性质
例2:(2008常州)若反比例函数的图象在其每个象限内,y随x的增大而减小,则k的值可以是( )
A.-1 B.3 C.0 D.-3
解答:B
例3:(2008新疆)在函数的图象上有三个点的坐标分别为(1,)、(,)、(,),函数值y1、y2、y3的大小关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y2<y1<y3 D.y3<y1<y2
解答:D
3、反比例函数的关系式
例4:(2008宁波)如图,正方形的边长为2,反比例函数过点,
则的值是( )
A. B. C. D.
解答:D
例5:(2009天津)已知图中的曲线是反比例函数(为常数)图象的一支.
(Ⅰ) 这个反比例函数图象的另一支在第几象限?常数的取值范围是什么?
(Ⅱ)若该函数的图象与正比例函数的图象在第一象内限的交点为,过点作轴的垂线,垂足为,当的面积为4时,求点的坐标及反比例函数的解析式.
解答:(Ⅰ)这个反比例函数图象的另一支在第三象限.
因为这个反比例函数的图象分布在第一、第三象限,
所以,解得.
(Ⅱ)如图,由第一象限内的点在正比例函数的图象上,
设点的坐标为,则点的坐标为,
,解得(负值舍去).
点的坐标为.
又点在反比例函数的图象上,
,即.
反比例函数的解析式为.
4、反比例函数的应用
例6:(2007安徽)一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为x、y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( )
解答:A
例7:(2008巴中)为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量(mg)与燃烧时间(分钟)成正比例;燃烧后,与成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
(1)求药物燃烧时与的函数关系式.
(2)求药物燃烧后与的函数关系式.
(3)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室?
解答:(1)设药物燃烧阶段函数解析式为,由题意得:
.此阶段函数解析式为
(2)设药物燃烧结束后的函数解析式为,由题意得:
.此阶段函数解析式为
(3)当时,得
从消毒开始经过50分钟后学生才可回教室.
真题训练
1、(2007南昌)对于反比例函数,下列说法不正确的是( )
A.点在它的图象上 B.它的图象在第一、三象限
C.当时,随的增大而增大 D.当时,随的增大而减小
2、(2009青岛)一块蓄电池的电压为定值,使用此蓄电池为电源时,电流(A)与电阻(Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过10A,那么此用电器的可变电阻应( )
A.不小于4.8Ω B.不大于4.8Ω C.不小于14Ω D.不大于14Ω
3、(2009泰安)如图,双曲线经过矩形QABC的边BC的中点E,交AB于点D。若梯形ODBC的面积为3,则双曲线的解析式为( )
A. B. C. D.
4、(2007孝感)在反比例函数图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k>3 B.k>0 C.k<3 D. k<0
5、(2008济南)如图:等腰直角三角形ABC位于第一象限,
AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,
且两条直角边AB、AC分别平行于x轴、y轴,若双曲线
(k≠0)与有交点,则k的取值范围是( )
A. B. C. D.
6、(2009铁岭)如图所示,反比例函数与正比例函数的图象的一个交点坐标是,若,则的取值范围在数轴上表示为( )
7、(2008河北)点在反比例函数的图象上,则 .
8、(2009山西)若反比例函数的表达式为,则当时,的取值范围是 .
9、(2009佳木斯)反比例函数的图象在每个象限内,随的增大而增大,则的值可以是 .(写出一个符合条件的实数即可)
10、(2008兰州)如图,已知双曲线()经过
矩形的边的中点,且四边形的
面积为2,则 .
11、(2009温州)如图,在平面直角坐标系中,直线AB与Y轴和X轴分别交于点A、点8,与反比例函数y一罟在第一象限的图象交于点c(1,6)、点D(3,x).过点C作CE上y轴于E,过点D作DF上X轴于F.
(1)求m,n的值;
(2)求直线AB的函数解析式;
(3)求证:△AEC∽△DFB.
12、(2009兰州)如图,已知 HYPERLINK "http://www." EMBED Equation.DSMT4 ,是一次函数的图象和反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线与轴的交点的坐标及△的面积;
(3)求方程的解(请直接写出答案);
(4)求不等式的解集(请直接写出答案).
13、(2009河池)为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量(毫克)与时间(分钟)成正比例;药物释放完毕后,与成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,与之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
14、(2009舟山)水产公司有一种海产品共2 104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:
第1天 第2天 第3天 第4天 第5天 第6天 第7天 第8天
售价x(元/千克) 400 250 240 200 150 125 120
销售量y(千克) 30 40 48 60 80 96 100
观察表中数据,发现可以用反比例函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系.
(1) 写出这个反比例函数的解析式,并补全表格;
(2) 在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
(3) 在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?
参考答案
真题训练
题号 1 2 3 4 5 6
答案 C A B A C D
7、2
8、
9、(符合题意即可)
10、2
11、
12、解:(1)在函数的图象上
.
反比例函数的解析式为:.
点在函数的图象上
经过,,
解之得
一次函数的解析式为:
(2)是直线与轴的交点
当时,
点
(3)
(4)
13、解:(1)药物释放过程中与的函数关系式为
(0≤≤12)
药物释放完毕后与的函数关系式为(≥12)
(2) 解之,得 (分钟)(小时)
答: 从药物释放开始,至少需要经过4小时后,学生才能进入教室.
14、解:(1) 函数解析式为.
填表如下:
第1天 第2天 第3天 第4天 第5天 第6天 第7天 第8天
售价x(元/千克) 400 300 250 240 200 150 125 120
销售量y(千克) 30 40 48 50 60 80 96 100
(2) 2 104-(30+40+48+50+60+80+96+100)=1 600,
即8天试销后,余下的海产品还有1 600千克.
当x=150时,=80.
1 600÷80=20,所以余下的这些海产品预计再用20天可以全部售出.
(3) 1 600-80×15=400,400÷2=200,
即如果正好用2天售完,那么每天需要售出200千克.
当y=200时, ( http: / / www. / )=60.
所以新确定的价格最高不超过60元/千克才能完成销售任务.
C
E
B
A
F
O
x
y
(分钟)
12
x
y=2x
A
B
O
y
x
O
y
D.
0
2
1
C.
0
2
1
B.
0
2
1
0
2
A.
1
第6题图
8
I/A
R/Ω
O
6
O
x
y1
y2
第5题图
C
B
A
O
x
1
y
1
2
2
1
y
(毫克)
9
O
B
A
O
C
y
x
PAGE
7
同课章节目录
