冲刺2010中考复习(10)图形的初步认识
文档属性
| 名称 | 冲刺2010中考复习(10)图形的初步认识 |  | |
| 格式 | zip | ||
| 文件大小 | 383.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-30 20:19:00 | ||
图片预览


文档简介
本系列资料系2010中考复习精品资料,每一篇内容分为三个版块:内容解读、考点剖析、真题训练,精选近几年各地中考题,适合全层次初三学生系统复习初中数学知识。
冲刺2010中考复习(10)
第十讲 图形的初步认识
内容解读
图形的认识是历届中考的基础考点,学生应掌握:线段、射线、直线的性质,角的基础知识与基本计算;平行线的性质和判定。
考点剖析
1、线段、射线、直线的性质
例1:(2009云南)如图,点C是线段AB上的点,点D是线段BC的中点,若AB=10,AC=6 ,则CD=_______________.
解答:2
2、角的基本性质
例2:(2006河南)两条直线相交所成的四个角中,下列说法正确的是( )
A.一定有一个锐角B.一定有一个钝角 C.一定有一个直角 D.一定有一个不是钝角
解答:D
例3:(2008永州)一个角的补角是这个角的余角的3倍,则这个角为度 .
解答:45°
3、同位角、内错角和同旁内角
例4:(2009桂林)如图,在所标识的角中,同位角是( )
A.和 B.和
C.和 D.和
解答:C
4、平行线的性质
例5:(2009安徽)如图,直线l1∥l2,则α为( )
A.150° B.140° C.130° D.120°
解答:D
例6:(2008孝感)如图,分别在上,为两平行线间一点,那么( )
A. B. C. D.
解答:C
5、平行线的判定
例7:(2008永州)如图,直线a、b被直线c所截,若要a∥b,需增加条件 (填一个即可).
解答:或或
6、平行线的综合运用
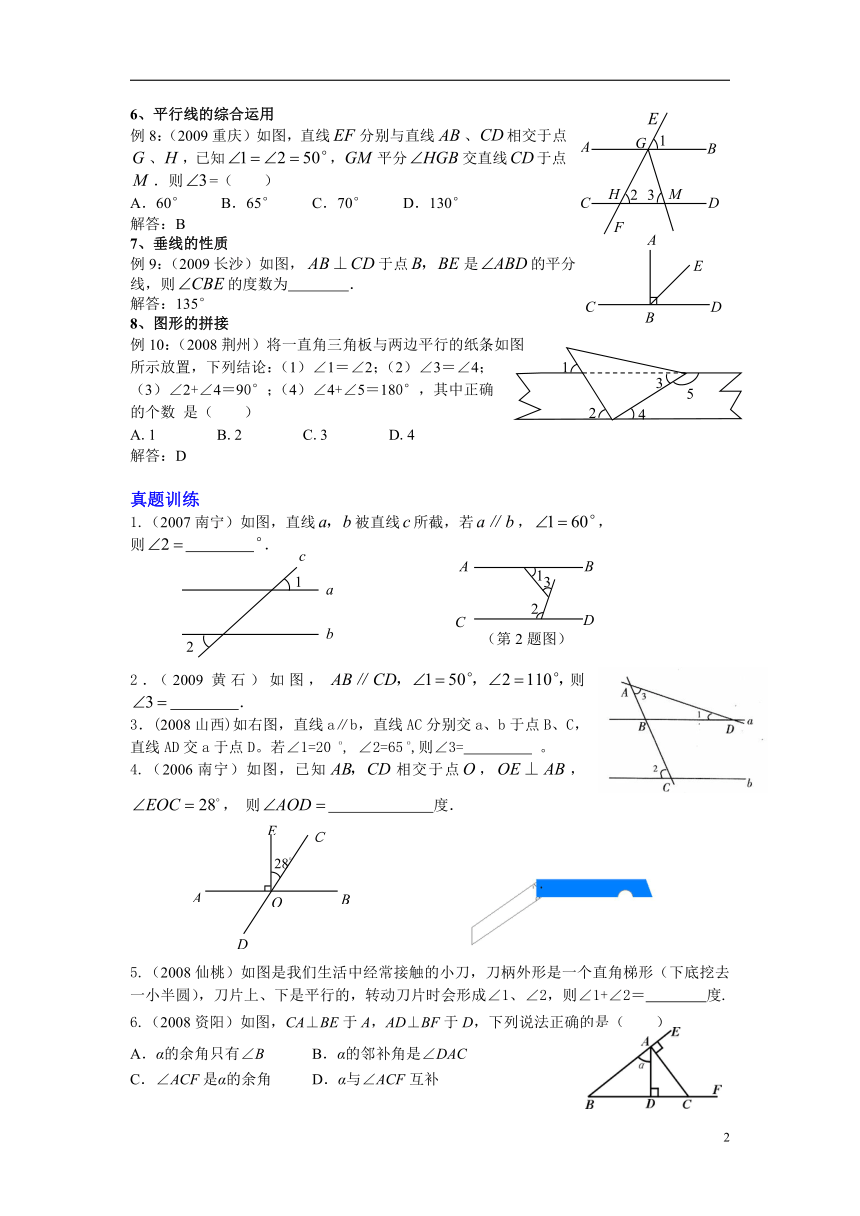
例8:(2009重庆)如图,直线分别与直线、相交于点、,已知,平分交直线于点.则=( )
A.60° B.65° C.70° D.130°
解答:B
7、垂线的性质
例9:(2009长沙)如图,于点是的平分
线,则的度数为 .
解答:135°
8、图形的拼接
例10:(2008荆州)将一直角三角板与两边平行的纸条如图
所示放置,下列结论:(1)∠1=∠2;(2)∠3=∠4;
(3)∠2+∠4=90°;(4)∠4+∠5=180°,其中正确
的个数 是( )
A.1 B.2 C.3 D.4
解答:D
真题训练
1.(2007南宁)如图,直线被直线所截,若,,
则 .
2.(2009黄石)如图,则 .
3.(2008山西)如右图,直线a∥b,直线AC分别交a、b于点B、C,直线AD交a于点D。若∠1=20 o, ∠2=65 o,则∠3= 。
4.(2006南宁)如图,已知相交于点,,, 则 度.
5.(2008仙桃)如图是我们生活中经常接触的小刀,刀柄外形是一个直角梯形(下底挖去一小半圆),刀片上、下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2= 度.
6.(2008资阳)如图,CA⊥BE于A,AD⊥BF于D,下列说法正确的是( )
A.α的余角只有∠B B.α的邻补角是∠DAC
C.∠ACF是α的余角 D.α与∠ACF互补
7.(2008烟台)如图,小明从A 处出发沿北偏东60°向行走至B处,又沿北偏西20°方向行走至 C 处,此时需把方向调整到与出发时一致,则方向的调整应是( )
A.右转80° B.左传80° C.右转100° D.左传100°
8.(2007绍兴)学行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如上图(1)~(4) ):
从图中可知,小敏画平行线的依据有( )
①两直线平行,同位角相等; ②两直线平行,内错角相等;
③同位角相等,两直线平行; ④内错角相等,两直线平行.
A.①② B.②③ C.③④ D.①④
9.(2009崇左)如图,把矩形沿对折后使两部分重合,若,则=( )
A.110° B.115° C.120° D.130°
10.(2008杭州)设一个锐角与这个角的补角的差的绝对值为,则( )
A. 0°<<90° B. 0°<≤90°
C. 0°<<90°或90°<<180° D. 0°<<180°
11.(2006河南)如图,线段AB=4,点O是线段AB上的点,点C、D是线段OA、OB的中点,小明很轻松地求得CD=2.他在反思过程中突发奇想:若点O运动到线段AB的延长线上或直线AB外,原有的结论“CD=2”是仍然成立呢?请帮小明画出图形分析,并说明理由.
12.(2009淄博)如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37 ,求∠D的度数.
13.(2008衢州)如图,AB∥CD
(1)用直尺和圆规作的平分线CP,CP交AB于点E(保留作图痕迹,不写作法)
(2)在(1)中作出的线段CE上取一点F,连结AF。要使△ACF≌△AEF,还需要添加一个什么条件?请你写出这个条件(只要给出一种情况即可;图中不再增加字母和线段;不要求证明)。
14.(2007福州)如图,直线AC∥BD,连结AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分。当动点P落在某个部分时,连结PA、PB,构成∠PAC、∠APB、∠PBD三个角。(提示:有公共端点的两条重合的射线所组成的角是0°)
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立(直接回答成立或不成立)?
(3)当动点P落在第③部分时,全面探究∠PAC、∠APB、∠PBD之间的关系,并写出动点P的具体位置和相应的结论。选择其中一种结论加以证明。
参考答案
真题训练
1. 60 2. 60° 3.45 o 4.62 5.90
6.D 7.A 8.D 9.B 10.D
11.
12. 解: ∵AB∥CD, ∠A=37 ,
∴∠ECD=∠A=37 .
∵DE⊥AE,
∴∠D=90 –∠ECD=90 –37 =53 .
13. 解:(1)作图略;
(2)取点F和画AF正确(如图);
添加的条件可以是:F是CE的中点;
AF⊥CE;∠CAF=∠EAF等。(选一个即可)
14. (1)解法一:如图9-1
延长BP交直线AC于点E
∵ AC∥BD , ∴ ∠PEA = ∠PBD .
∵ ∠APB = ∠PAE + ∠PEA ,
∴ ∠APB = ∠PAC + ∠PBD .
解法二:如图9-2
过点P作FP∥AC ,
∴ ∠PAC = ∠APF .
∵ AC∥BD , ∴FP∥BD .
∴ ∠FPB =∠PBD .
∴ ∠APB =∠APF +∠FPB =∠PAC + ∠PBD .
解法三:如图9-3,
∵ AC∥BD , ∴ ∠CAB +∠ABD = 180°
即 ∠PAC +∠PAB +∠PBA +∠PBD = 180°.
又∠APB +∠PBA +∠PAB = 180°,
∴ ∠APB =∠PAC +∠PBD .
(2)不成立.
(3)(a)当动点P在射线BA的右侧时,结论是
∠PBD=∠PAC+∠APB .
(b)当动点P在射线BA上,
结论是∠PBD =∠PAC +∠APB .
或∠PAC =∠PBD +∠APB 或 ∠APB = 0°,
∠PAC =∠PBD(任写一个即可).
(c) 当动点P在射线BA的左侧时,
结论是∠PAC =∠APB +∠PBD .
选择(a) 证明:
如图9-4,连接PA,连接PB交AC于M
∵ AC∥BD ,
∴ ∠PMC =∠PBD .
又∵∠PMC =∠PAM +∠APM ,
∴ ∠PBD =∠PAC +∠APB .
选择(b) 证明:如图9-5
∵ 点P在射线BA上,∴∠APB = 0°.
∵ AC∥BD , ∴∠PBD =∠PAC .
∴ ∠PBD =∠PAC +∠APB
或∠PAC =∠PBD+∠APB
或∠APB = 0°,∠PAC =∠PBD.
选择(c) 证明:
如图9-6,连接PA,连接PB交AC于F
∵ AC∥BD , ∴∠PFA =∠PBD .
∵ ∠PAC =∠APF +∠PFA ,
∴ ∠PAC =∠APB +∠PBD .
F
H
C
B
D
E
A
3
2
1
130°
A
D
C
G
B
A
(例4图)
4
④
③
②
①
B
A
④
③
②
①
B
A
B
C
D
E
A
1
C
D
F
P
E
B
A
C
D
A
B
E
D
1
(第2题图)
C
D
B
A
(第9题)
F
C
O
2
1
B
D
C
A
D
B
E
b
a
c
C
B
A
5
4
3
2
1
3
2
M
3
2
1
N
P
M
b
a
A
l2
l1
α
70°
3
2
1
B
①
②
③
④
P
(第14题图)
C
D
C
D
C
D
PAGE
1
冲刺2010中考复习(10)
第十讲 图形的初步认识
内容解读
图形的认识是历届中考的基础考点,学生应掌握:线段、射线、直线的性质,角的基础知识与基本计算;平行线的性质和判定。
考点剖析
1、线段、射线、直线的性质
例1:(2009云南)如图,点C是线段AB上的点,点D是线段BC的中点,若AB=10,AC=6 ,则CD=_______________.
解答:2
2、角的基本性质
例2:(2006河南)两条直线相交所成的四个角中,下列说法正确的是( )
A.一定有一个锐角B.一定有一个钝角 C.一定有一个直角 D.一定有一个不是钝角
解答:D
例3:(2008永州)一个角的补角是这个角的余角的3倍,则这个角为度 .
解答:45°
3、同位角、内错角和同旁内角
例4:(2009桂林)如图,在所标识的角中,同位角是( )
A.和 B.和
C.和 D.和
解答:C
4、平行线的性质
例5:(2009安徽)如图,直线l1∥l2,则α为( )
A.150° B.140° C.130° D.120°
解答:D
例6:(2008孝感)如图,分别在上,为两平行线间一点,那么( )
A. B. C. D.
解答:C
5、平行线的判定
例7:(2008永州)如图,直线a、b被直线c所截,若要a∥b,需增加条件 (填一个即可).
解答:或或
6、平行线的综合运用
例8:(2009重庆)如图,直线分别与直线、相交于点、,已知,平分交直线于点.则=( )
A.60° B.65° C.70° D.130°
解答:B
7、垂线的性质
例9:(2009长沙)如图,于点是的平分
线,则的度数为 .
解答:135°
8、图形的拼接
例10:(2008荆州)将一直角三角板与两边平行的纸条如图
所示放置,下列结论:(1)∠1=∠2;(2)∠3=∠4;
(3)∠2+∠4=90°;(4)∠4+∠5=180°,其中正确
的个数 是( )
A.1 B.2 C.3 D.4
解答:D
真题训练
1.(2007南宁)如图,直线被直线所截,若,,
则 .
2.(2009黄石)如图,则 .
3.(2008山西)如右图,直线a∥b,直线AC分别交a、b于点B、C,直线AD交a于点D。若∠1=20 o, ∠2=65 o,则∠3= 。
4.(2006南宁)如图,已知相交于点,,, 则 度.
5.(2008仙桃)如图是我们生活中经常接触的小刀,刀柄外形是一个直角梯形(下底挖去一小半圆),刀片上、下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2= 度.
6.(2008资阳)如图,CA⊥BE于A,AD⊥BF于D,下列说法正确的是( )
A.α的余角只有∠B B.α的邻补角是∠DAC
C.∠ACF是α的余角 D.α与∠ACF互补
7.(2008烟台)如图,小明从A 处出发沿北偏东60°向行走至B处,又沿北偏西20°方向行走至 C 处,此时需把方向调整到与出发时一致,则方向的调整应是( )
A.右转80° B.左传80° C.右转100° D.左传100°
8.(2007绍兴)学行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如上图(1)~(4) ):
从图中可知,小敏画平行线的依据有( )
①两直线平行,同位角相等; ②两直线平行,内错角相等;
③同位角相等,两直线平行; ④内错角相等,两直线平行.
A.①② B.②③ C.③④ D.①④
9.(2009崇左)如图,把矩形沿对折后使两部分重合,若,则=( )
A.110° B.115° C.120° D.130°
10.(2008杭州)设一个锐角与这个角的补角的差的绝对值为,则( )
A. 0°<<90° B. 0°<≤90°
C. 0°<<90°或90°<<180° D. 0°<<180°
11.(2006河南)如图,线段AB=4,点O是线段AB上的点,点C、D是线段OA、OB的中点,小明很轻松地求得CD=2.他在反思过程中突发奇想:若点O运动到线段AB的延长线上或直线AB外,原有的结论“CD=2”是仍然成立呢?请帮小明画出图形分析,并说明理由.
12.(2009淄博)如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37 ,求∠D的度数.
13.(2008衢州)如图,AB∥CD
(1)用直尺和圆规作的平分线CP,CP交AB于点E(保留作图痕迹,不写作法)
(2)在(1)中作出的线段CE上取一点F,连结AF。要使△ACF≌△AEF,还需要添加一个什么条件?请你写出这个条件(只要给出一种情况即可;图中不再增加字母和线段;不要求证明)。
14.(2007福州)如图,直线AC∥BD,连结AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分。当动点P落在某个部分时,连结PA、PB,构成∠PAC、∠APB、∠PBD三个角。(提示:有公共端点的两条重合的射线所组成的角是0°)
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立(直接回答成立或不成立)?
(3)当动点P落在第③部分时,全面探究∠PAC、∠APB、∠PBD之间的关系,并写出动点P的具体位置和相应的结论。选择其中一种结论加以证明。
参考答案
真题训练
1. 60 2. 60° 3.45 o 4.62 5.90
6.D 7.A 8.D 9.B 10.D
11.
12. 解: ∵AB∥CD, ∠A=37 ,
∴∠ECD=∠A=37 .
∵DE⊥AE,
∴∠D=90 –∠ECD=90 –37 =53 .
13. 解:(1)作图略;
(2)取点F和画AF正确(如图);
添加的条件可以是:F是CE的中点;
AF⊥CE;∠CAF=∠EAF等。(选一个即可)
14. (1)解法一:如图9-1
延长BP交直线AC于点E
∵ AC∥BD , ∴ ∠PEA = ∠PBD .
∵ ∠APB = ∠PAE + ∠PEA ,
∴ ∠APB = ∠PAC + ∠PBD .
解法二:如图9-2
过点P作FP∥AC ,
∴ ∠PAC = ∠APF .
∵ AC∥BD , ∴FP∥BD .
∴ ∠FPB =∠PBD .
∴ ∠APB =∠APF +∠FPB =∠PAC + ∠PBD .
解法三:如图9-3,
∵ AC∥BD , ∴ ∠CAB +∠ABD = 180°
即 ∠PAC +∠PAB +∠PBA +∠PBD = 180°.
又∠APB +∠PBA +∠PAB = 180°,
∴ ∠APB =∠PAC +∠PBD .
(2)不成立.
(3)(a)当动点P在射线BA的右侧时,结论是
∠PBD=∠PAC+∠APB .
(b)当动点P在射线BA上,
结论是∠PBD =∠PAC +∠APB .
或∠PAC =∠PBD +∠APB 或 ∠APB = 0°,
∠PAC =∠PBD(任写一个即可).
(c) 当动点P在射线BA的左侧时,
结论是∠PAC =∠APB +∠PBD .
选择(a) 证明:
如图9-4,连接PA,连接PB交AC于M
∵ AC∥BD ,
∴ ∠PMC =∠PBD .
又∵∠PMC =∠PAM +∠APM ,
∴ ∠PBD =∠PAC +∠APB .
选择(b) 证明:如图9-5
∵ 点P在射线BA上,∴∠APB = 0°.
∵ AC∥BD , ∴∠PBD =∠PAC .
∴ ∠PBD =∠PAC +∠APB
或∠PAC =∠PBD+∠APB
或∠APB = 0°,∠PAC =∠PBD.
选择(c) 证明:
如图9-6,连接PA,连接PB交AC于F
∵ AC∥BD , ∴∠PFA =∠PBD .
∵ ∠PAC =∠APF +∠PFA ,
∴ ∠PAC =∠APB +∠PBD .
F
H
C
B
D
E
A
3
2
1
130°
A
D
C
G
B
A
(例4图)
4
④
③
②
①
B
A
④
③
②
①
B
A
B
C
D
E
A
1
C
D
F
P
E
B
A
C
D
A
B
E
D
1
(第2题图)
C
D
B
A
(第9题)
F
C
O
2
1
B
D
C
A
D
B
E
b
a
c
C
B
A
5
4
3
2
1
3
2
M
3
2
1
N
P
M
b
a
A
l2
l1
α
70°
3
2
1
B
①
②
③
④
P
(第14题图)
C
D
C
D
C
D
PAGE
1
同课章节目录
