3.2 简单图形的坐标表示 学案(无答案)
文档属性
| 名称 | 3.2 简单图形的坐标表示 学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 144.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-20 00:00:00 | ||
图片预览

文档简介
3.2
简单图形的坐标表示
学案
学习目标
(一)教学知识点
能在方格纸上建立适当的直角坐标系,描述物体的位置;能结合具体情景灵活应用多种方式确定物体的位置.
(二)能力目标
根据已知条件有不同的解决问题的方式,灵活地选取既简便又易懂的方法求解是本节的重点,通过多角度的探索既可以拓宽学生的思维,又可以从中找到解决问题的捷径,使大家的解决问题的能力得以提高.
(三)情感与价值观
培养学生重视实践,善于观察的习惯.
学习重点
建立适当的直角坐标系,确定点的位置.
学习难点
利用给定点的坐标建立直角坐标系.
学习过程
一、创设问题情境,引入新课:
出示一张以方格纸为背景的示意图,提出问题:请你以某个景点为原点,画出直角坐标系,并向大家介绍其他景点的位置.
二、讲授新课
如下图,矩形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标.
分析:在没有直角坐标系的情况下是不能写出各个顶点的坐标的,所以应先建立直角坐标系,那么应如何选取直角坐标系呢?请大家思考.
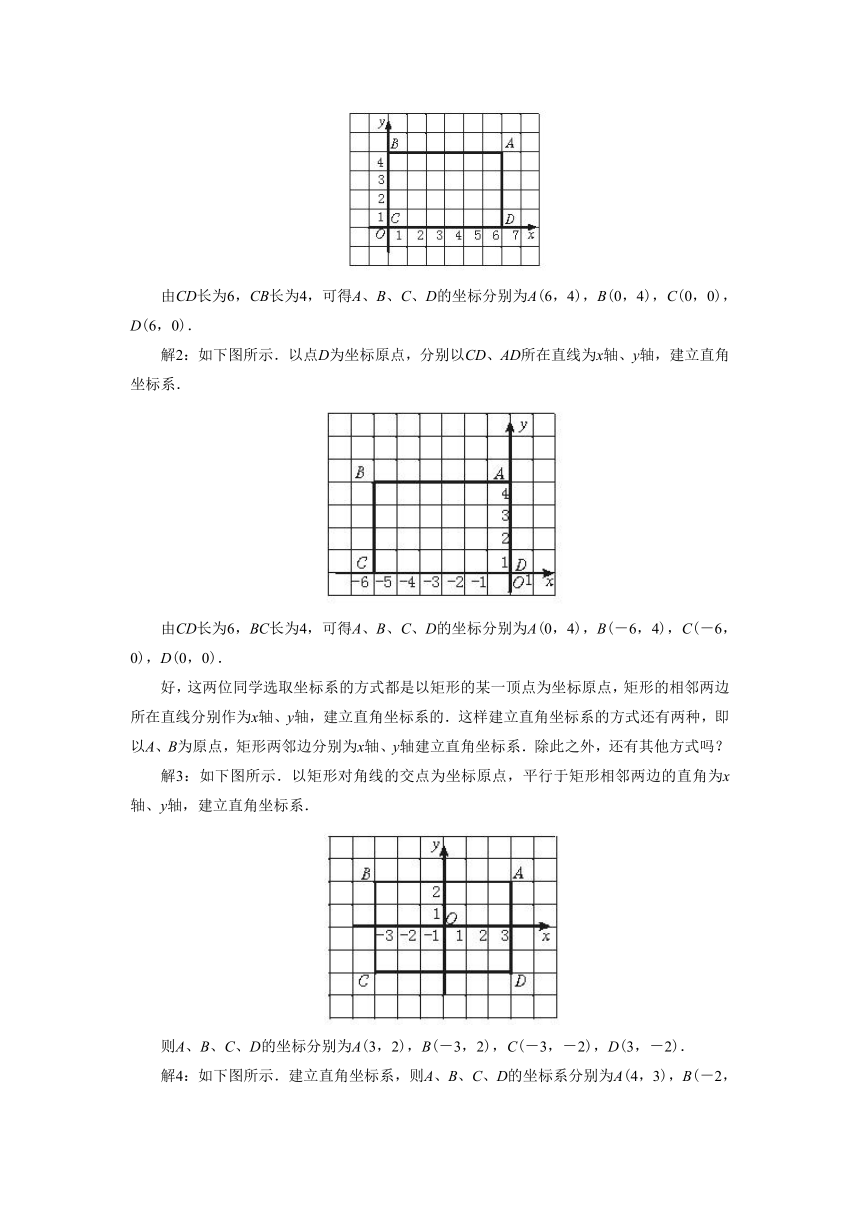
解1:如下图所示,以点C为坐标原点,分别以CD、CB所在直线为x轴、y轴,建立直角坐标系.
由CD长为6,CB长为4,可得A、B、C、D的坐标分别为A(6,4),B(0,4),C(0,0),D(6,0).
解2:如下图所示.以点D为坐标原点,分别以CD、AD所在直线为x轴、y轴,建立直角坐标系.
由CD长为6,BC长为4,可得A、B、C、D的坐标分别为A(0,4),B(-6,4),C(-6,0),D(0,0).
好,这两位同学选取坐标系的方式都是以矩形的某一顶点为坐标原点,矩形的相邻两边所在直线分别作为x轴、y轴,建立直角坐标系的.这样建立直角坐标系的方式还有两种,即以A、B为原点,矩形两邻边分别为x轴、y轴建立直角坐标系.除此之外,还有其他方式吗?
解3:如下图所示.以矩形对角线的交点为坐标原点,平行于矩形相邻两边的直角为x轴、y轴,建立直角坐标系.
则A、B、C、D的坐标分别为A(3,2),B(-3,2),C(-3,-2),D(3,-2).
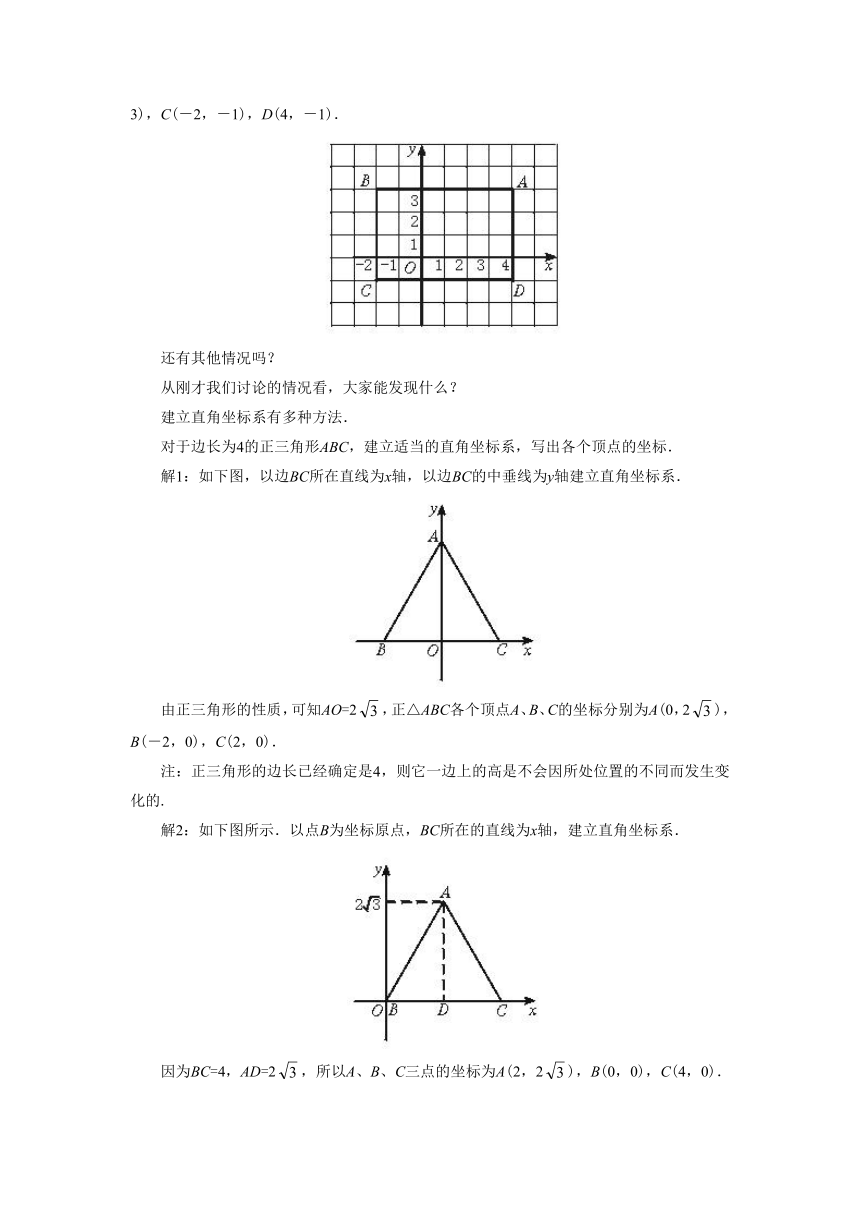
解4:如下图所示.建立直角坐标系,则A、B、C、D的坐标系分别为A(4,3),B(-2,3),C(-2,-1),D(4,-1).
还有其他情况吗?
从刚才我们讨论的情况看,大家能发现什么?
建立直角坐标系有多种方法.
对于边长为4的正三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标.
解1:如下图,以边BC所在直线为x轴,以边BC的中垂线为y轴建立直角坐标系.
由正三角形的性质,可知AO=2,正△ABC各个顶点A、B、C的坐标分别为A(0,2),B(-2,0),C(2,0).
注:正三角形的边长已经确定是4,则它一边上的高是不会因所处位置的不同而发生变化的.
解2:如下图所示.以点B为坐标原点,BC所在的直线为x轴,建立直角坐标系.
因为BC=4,AD=2,所以A、B、C三点的坐标为A(2,2),B(0,0),C(4,0).
也可以分别以A、C为坐标原点,以平行于线段BC或线段BC所在的直线为x轴,建立直角坐标系,则A、B、C的坐标相应地发生变化.
例题解析:
例1:如课本第92页图3-14,矩形ABCD的长和宽分别为8和6,试建立适当的平面直角坐标系表示矩形ABCD各顶点的坐标,并作出矩形ABCD.
例2:如课本第92页图3-16是一个机器零件的尺寸规格示意图,试建立适当的平面直角坐标系表示其各顶点的坐标,并作出这个示意图.
议一议:
在一次“寻宝”游戏中,寻宝人员已经找到了坐标为(3,2)和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4,4),除此外不知道其他信息.如何确定直角坐标系找到“宝藏”?与同伴进行交流.
三、课堂练习:书上的随堂练习.如下图,五个儿童正在做游戏,建立适当的直角坐标系,写出这五个儿童所在位置的坐标.
四、课时小节:本节课的目的是能在方格纸上建立适当的直角坐标系,描述物体的位置.
基础练习
1、分别说出下列各点在哪个象限内或在哪条坐标轴上?
A(6,-2),B(0,3),C(3,7),
D(-6,-3),E(-2,0),F(-9,5)
2、在直角坐标系中,描出下列各点:A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4)
(1)E点到原点O的距离是_______个单位长.
(2)点D到x轴的距离是_______,到y轴的距离是_______.点C呢?
思考:设点P的坐标为(a,b),则点P到x轴的距离为_________.
到y轴的距离为_________.
3、如图,建立平面直角坐标系,使点B,C的坐标分别为(0,0)和(4,0),写出点A,D,E,F,G的坐标,并指出它们所在的象限.
4、如图为风筝的图案.
(1)若原点用字母O表示,写出图中点A,B,C的坐标.
(2)试求(1)中风筝所覆盖的平面的面积.
5、三角形ABO是以OB为底的等腰三角形,点O为坐标原点,点B在x轴上,点B与坐标原点的距离为3,点A与x轴的距离为2,写出A,B的坐标.
6.如图,根据坐标平面内点的位置,写出以下各点的坐标:
A(
),B(
),C(
),D(
),E(
),F(
)
7.建立适当的平面直角坐标系,并在图中描出坐标
A(2,3),B(-2,3),C(3,-2),D(5,1),
E(0,-4),F(-3,0)的各点.
简单图形的坐标表示
学案
学习目标
(一)教学知识点
能在方格纸上建立适当的直角坐标系,描述物体的位置;能结合具体情景灵活应用多种方式确定物体的位置.
(二)能力目标
根据已知条件有不同的解决问题的方式,灵活地选取既简便又易懂的方法求解是本节的重点,通过多角度的探索既可以拓宽学生的思维,又可以从中找到解决问题的捷径,使大家的解决问题的能力得以提高.
(三)情感与价值观
培养学生重视实践,善于观察的习惯.
学习重点
建立适当的直角坐标系,确定点的位置.
学习难点
利用给定点的坐标建立直角坐标系.
学习过程
一、创设问题情境,引入新课:
出示一张以方格纸为背景的示意图,提出问题:请你以某个景点为原点,画出直角坐标系,并向大家介绍其他景点的位置.
二、讲授新课
如下图,矩形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标.
分析:在没有直角坐标系的情况下是不能写出各个顶点的坐标的,所以应先建立直角坐标系,那么应如何选取直角坐标系呢?请大家思考.
解1:如下图所示,以点C为坐标原点,分别以CD、CB所在直线为x轴、y轴,建立直角坐标系.
由CD长为6,CB长为4,可得A、B、C、D的坐标分别为A(6,4),B(0,4),C(0,0),D(6,0).
解2:如下图所示.以点D为坐标原点,分别以CD、AD所在直线为x轴、y轴,建立直角坐标系.
由CD长为6,BC长为4,可得A、B、C、D的坐标分别为A(0,4),B(-6,4),C(-6,0),D(0,0).
好,这两位同学选取坐标系的方式都是以矩形的某一顶点为坐标原点,矩形的相邻两边所在直线分别作为x轴、y轴,建立直角坐标系的.这样建立直角坐标系的方式还有两种,即以A、B为原点,矩形两邻边分别为x轴、y轴建立直角坐标系.除此之外,还有其他方式吗?
解3:如下图所示.以矩形对角线的交点为坐标原点,平行于矩形相邻两边的直角为x轴、y轴,建立直角坐标系.
则A、B、C、D的坐标分别为A(3,2),B(-3,2),C(-3,-2),D(3,-2).
解4:如下图所示.建立直角坐标系,则A、B、C、D的坐标系分别为A(4,3),B(-2,3),C(-2,-1),D(4,-1).
还有其他情况吗?
从刚才我们讨论的情况看,大家能发现什么?
建立直角坐标系有多种方法.
对于边长为4的正三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标.
解1:如下图,以边BC所在直线为x轴,以边BC的中垂线为y轴建立直角坐标系.
由正三角形的性质,可知AO=2,正△ABC各个顶点A、B、C的坐标分别为A(0,2),B(-2,0),C(2,0).
注:正三角形的边长已经确定是4,则它一边上的高是不会因所处位置的不同而发生变化的.
解2:如下图所示.以点B为坐标原点,BC所在的直线为x轴,建立直角坐标系.
因为BC=4,AD=2,所以A、B、C三点的坐标为A(2,2),B(0,0),C(4,0).
也可以分别以A、C为坐标原点,以平行于线段BC或线段BC所在的直线为x轴,建立直角坐标系,则A、B、C的坐标相应地发生变化.
例题解析:
例1:如课本第92页图3-14,矩形ABCD的长和宽分别为8和6,试建立适当的平面直角坐标系表示矩形ABCD各顶点的坐标,并作出矩形ABCD.
例2:如课本第92页图3-16是一个机器零件的尺寸规格示意图,试建立适当的平面直角坐标系表示其各顶点的坐标,并作出这个示意图.
议一议:
在一次“寻宝”游戏中,寻宝人员已经找到了坐标为(3,2)和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4,4),除此外不知道其他信息.如何确定直角坐标系找到“宝藏”?与同伴进行交流.
三、课堂练习:书上的随堂练习.如下图,五个儿童正在做游戏,建立适当的直角坐标系,写出这五个儿童所在位置的坐标.
四、课时小节:本节课的目的是能在方格纸上建立适当的直角坐标系,描述物体的位置.
基础练习
1、分别说出下列各点在哪个象限内或在哪条坐标轴上?
A(6,-2),B(0,3),C(3,7),
D(-6,-3),E(-2,0),F(-9,5)
2、在直角坐标系中,描出下列各点:A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4)
(1)E点到原点O的距离是_______个单位长.
(2)点D到x轴的距离是_______,到y轴的距离是_______.点C呢?
思考:设点P的坐标为(a,b),则点P到x轴的距离为_________.
到y轴的距离为_________.
3、如图,建立平面直角坐标系,使点B,C的坐标分别为(0,0)和(4,0),写出点A,D,E,F,G的坐标,并指出它们所在的象限.
4、如图为风筝的图案.
(1)若原点用字母O表示,写出图中点A,B,C的坐标.
(2)试求(1)中风筝所覆盖的平面的面积.
5、三角形ABO是以OB为底的等腰三角形,点O为坐标原点,点B在x轴上,点B与坐标原点的距离为3,点A与x轴的距离为2,写出A,B的坐标.
6.如图,根据坐标平面内点的位置,写出以下各点的坐标:
A(
),B(
),C(
),D(
),E(
),F(
)
7.建立适当的平面直角坐标系,并在图中描出坐标
A(2,3),B(-2,3),C(3,-2),D(5,1),
E(0,-4),F(-3,0)的各点.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
