2010年高三数学专题复习“数形结合思想”
文档属性
| 名称 | 2010年高三数学专题复习“数形结合思想” |
|
|
| 格式 | rar | ||
| 文件大小 | 273.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-05 00:00:00 | ||
图片预览








文档简介
课件20张PPT。热烈欢迎各位专家老师----------新 马 桥 中 学专题:"数形结合思想"
时间: 2010 年 4 月 23日
数形结合思想知识整合 数形结合就是根据数量关系与直观的图形之间的对应关系,通过数与形的相互转化来解决数学问题的一种重要思想方法,数形结合思想通过“以形助数”或“以数解形”,可使得复杂问题简单化,抽象问题具体化,从而将抽象思维转化为形象思维,有助于 把握数学问题的本质,它是数学的规律性与灵活性的有机结合。数形结合应用广泛,不仅在选择题、填空题中显示它的优越性,而且在解决一些抽象数学问题中常起到事半功倍的效果,数形结合的重点是研究“以形助数”,但“以数解形”在近年高考试题中也得到加强,应注意培养这种思想意识,要争取胸中有图,见数想图,以开拓自己的思维视野。数形结合思想应用方法1、在解方程与解不等式问题的应用2、在求函数的值域、最值问题中的应用3、在求复数和三角函数问题中的应用4、在向量和几何中的应用1.与方程有关的问题例1 解析:作出两个函数图象,易知两图象只有两个交点,故方程有2个实根 A. 1个 B. 2个 C. 3个 D. 1个或2个或3个 ( )。 B点拨: 对于一些不规则方程判断根的个数问题,用解方程的方法求出解来,再说有几个根是不可能的,而借助数形结合,将根的个数问题转化为图像的交点个数问题.yox1y=a│x│y=│log x│a练习:(08年高考湖北卷文13)方程的实数解的个数为 。解析: 如图,在同一坐标系内分别画出和的图象由图可知,两函数图象有两个交点,
即方程有两个根。2例2、若对任意x∈R ,不等式│X│≥ax恒
成立实数a的取值范围是()
A、 a<-1 B、│a│≦1
C、│a│<1 D、 a≥1
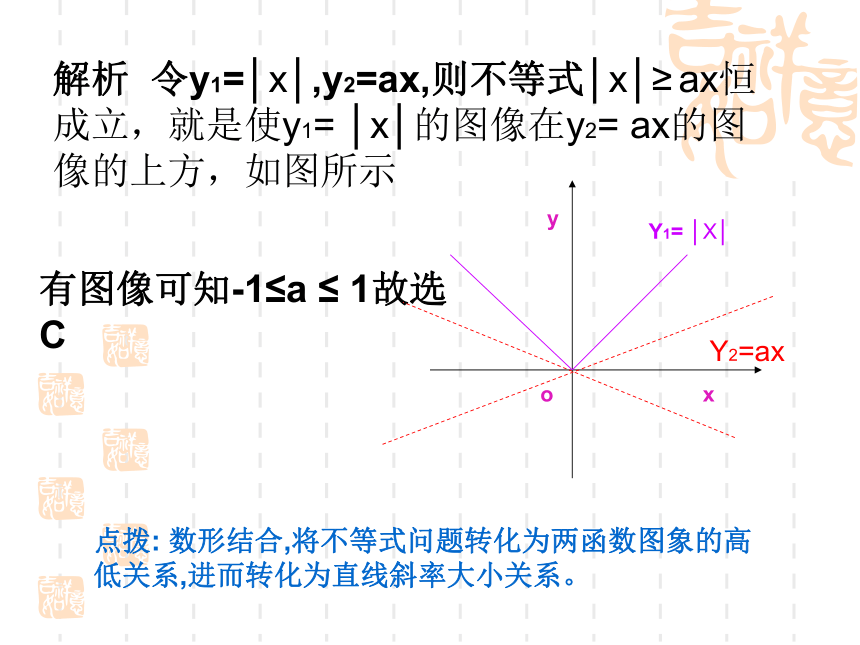
2、与不等式有关的问题解析 令y1=│x│,y2=ax,则不等式│x│≥ ax恒成立,就是使y1= │x│的图像在y2= ax的图像的上方,如图所示Y1= │X│Y2=axyxo有图像可知-1≤a ≤ 1故选C点拨: 数形结合,将不等式问题转化为两函数图象的高低关系,进而转化为直线斜率大小关系。练习解析:
. 点拨: 数形结合,将不等式问题转化为两函数图象的高低关系,进而转化为解方程,求交点的横坐标.例3已知函数f(x)(0≤x≦1)的图像是一段圆弧(如图所示)。若0B C D 以上都不对。A3 与函数有关的问题解析 构造函数g(x)= ,其几何意义是过曲线y=f(x)上的点(x,f(x))与原点(0,0)的直线的斜率。由图像可知,x由0到1变化时斜率逐渐减小,即g(x)为减函数。0点拨:通过构造一个函数,利用代数式的几何意义,
由斜率的递减得函数的单调性,将不等式中大小
比较转化为由函数单调性,巧妙地进行判别,
在这里构造函数是关键,数形结合是解题的法宝。A(x1,f(x1))B(x2,f(x2))x1x24、与几何有关的问题例4 截距。反思:对于形如y-3x的二元一次函数求最值,如果限制条件是表示的是几何区域或曲线,常采用借助直线的截距来求.解析( )DA 4√2, 0B 4, 4√2C 16, 0 D 4, 0点拨 由于向量具有双重性,既有代数的一面,又有几何的一面,因此利用它的几何意义解决选择题与填空题更直观,更简捷b课堂小结(一)利用函数图象性质解题(二)利用曲线方程图象的性质解题(三)利用几何图形的性质解题 本节主要讨论了利用数形结合思想来解决一些抽象数学问题的题型和方法: 数形结合的重点在于“以形助数”,通过“以形助数”使得复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的。练习解答1x分析:构造两个函数y= -a 与y= - +2x
由两个函数交点个数求得方程解的个数1)a>12)0由两个函数交点个数求得方程解的个数(1)a >1时xyo(2)0 N={ (x,y)| y= x + b},若M∩N=φ 则b满足 。分析:点集M表示的图形是半圆,点集N表示为直线,它随b值变化位置不断变化。本题即转化为b取何值时两图形没有公共点,由图形变化可得结论。xyoy=x+b即b>3 或b< -3问题:b取何值时M∩N分别有两个子集;四个子集。b3l1l2l3M={(x,y)|x=3cosθ,y=3sinθ,0 θ π },N={ (x,y)| y= x + b}练习(07年高考浙江卷理10)设g(x)是二次函数,若f(g(x)),则g(x)的值域是( )的值域是ABCD解析:C, 因为 g(x)是二次函数,值域不会是A、B,画出函数y=f(x)的图像(图1)易知,当g(x)值域是[0, ∞)时,f(g(x))[0,的值域是[0, ∞) 。点评:本题主要考查分段函数、复合函数、二次函数的图象和性质,通过函数的图象确定解题思路,直观、清晰,体现了数形结合的优越性。谢谢!再见!
时间: 2010 年 4 月 23日
数形结合思想知识整合 数形结合就是根据数量关系与直观的图形之间的对应关系,通过数与形的相互转化来解决数学问题的一种重要思想方法,数形结合思想通过“以形助数”或“以数解形”,可使得复杂问题简单化,抽象问题具体化,从而将抽象思维转化为形象思维,有助于 把握数学问题的本质,它是数学的规律性与灵活性的有机结合。数形结合应用广泛,不仅在选择题、填空题中显示它的优越性,而且在解决一些抽象数学问题中常起到事半功倍的效果,数形结合的重点是研究“以形助数”,但“以数解形”在近年高考试题中也得到加强,应注意培养这种思想意识,要争取胸中有图,见数想图,以开拓自己的思维视野。数形结合思想应用方法1、在解方程与解不等式问题的应用2、在求函数的值域、最值问题中的应用3、在求复数和三角函数问题中的应用4、在向量和几何中的应用1.与方程有关的问题例1 解析:作出两个函数图象,易知两图象只有两个交点,故方程有2个实根 A. 1个 B. 2个 C. 3个 D. 1个或2个或3个 ( )。 B点拨: 对于一些不规则方程判断根的个数问题,用解方程的方法求出解来,再说有几个根是不可能的,而借助数形结合,将根的个数问题转化为图像的交点个数问题.yox1y=a│x│y=│log x│a练习:(08年高考湖北卷文13)方程的实数解的个数为 。解析: 如图,在同一坐标系内分别画出和的图象由图可知,两函数图象有两个交点,
即方程有两个根。2例2、若对任意x∈R ,不等式│X│≥ax恒
成立实数a的取值范围是()
A、 a<-1 B、│a│≦1
C、│a│<1 D、 a≥1
2、与不等式有关的问题解析 令y1=│x│,y2=ax,则不等式│x│≥ ax恒成立,就是使y1= │x│的图像在y2= ax的图像的上方,如图所示Y1= │X│Y2=axyxo有图像可知-1≤a ≤ 1故选C点拨: 数形结合,将不等式问题转化为两函数图象的高低关系,进而转化为直线斜率大小关系。练习解析:
. 点拨: 数形结合,将不等式问题转化为两函数图象的高低关系,进而转化为解方程,求交点的横坐标.例3已知函数f(x)(0≤x≦1)的图像是一段圆弧(如图所示)。若0
由斜率的递减得函数的单调性,将不等式中大小
比较转化为由函数单调性,巧妙地进行判别,
在这里构造函数是关键,数形结合是解题的法宝。A(x1,f(x1))B(x2,f(x2))x1x24、与几何有关的问题例4 截距。反思:对于形如y-3x的二元一次函数求最值,如果限制条件是表示的是几何区域或曲线,常采用借助直线的截距来求.解析( )DA 4√2, 0B 4, 4√2C 16, 0 D 4, 0点拨 由于向量具有双重性,既有代数的一面,又有几何的一面,因此利用它的几何意义解决选择题与填空题更直观,更简捷b课堂小结(一)利用函数图象性质解题(二)利用曲线方程图象的性质解题(三)利用几何图形的性质解题 本节主要讨论了利用数形结合思想来解决一些抽象数学问题的题型和方法: 数形结合的重点在于“以形助数”,通过“以形助数”使得复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的。练习解答1x分析:构造两个函数y= -a 与y= - +2x
由两个函数交点个数求得方程解的个数1)a>12)0
同课章节目录
