选修1-2 数系的扩充
图片预览






文档简介
课件14张PPT。3.1 数系的扩充和复数的概念从社会生活来看,数的概念是从实践中产生和发展起
来的,人类早在蒙昧时代就已具有识别事物多寡的
能力,从这种原始“数觉”到抽象的“数”概念的形成,
是一个缓慢的、渐进的过程。开始时用手指计数,
当手指不敷运用时,用小石子检查放牧归来的羊的
只数,出现了石子记数;用结绳的方法统计猎物的
个数,称为结绳记数;用在木头上刻道的方法记录
捕鱼的数量为刻痕记数等等。
为了记数的需要产生了自然数,为了测量产生了
分数,为了刻画相反意义的数产生了负数,为解决
度量正方形对角线长的问题出现了无理数。一 数系的扩充从数学内部来看,数集是在按某种“规则”不断扩充的。在
自然数集中,加法和乘法总可以实施。由于小数不能减大数,
要使x+4=0有解,从而引入_______.自然数集扩充到整数集;
在整数集中,加法、减法和乘法总可以实施。由于除法只能
解决整除问题,要使方程3x-2=0有解,为此引入________.
整数集扩充到有理数集;在有理数集里加、减、乘和除(除数
不为零)总可实施;要使x2-2=0有解,为此引入________,有
理数扩充到实数集。思考1:以上数系扩充的过程是___________________.每一次数的概念发展,都是在原来数集基础上“添加”一种新
的数得来在新的数集中,原来的运算和性质仍然使用。同时
解决了某些运算在原来数集中不是总可以实施的矛盾。无理数分数负数思考2:在实数集中,方程x2+1=0无解,为使方程x2+1=0有解
,实数集应怎样扩充呢?为此,我们引入一个新数 , 叫做虚数单位,并规定: (1)它的平方等于 -1,即新授课(2)实数可以与它进行四则运算,进行四则运算时,原有的加、乘运算律仍然成立. 二.复数的有关概念 复数z=a+bi(a, b∈R)由两部分组成,实数a与b分别称为复数a+bi的实部与虚部,1与i分别是实数单位和虚数单位 形如 a+bi (a,b∈R)的数叫做复数. 其中i 叫做虚数
单位,由全体复数组成的集合C={a+bi}叫做复数集.
说明:
复数常用字母z 表示,即z=a+bi (a,b∈R)叫复数的
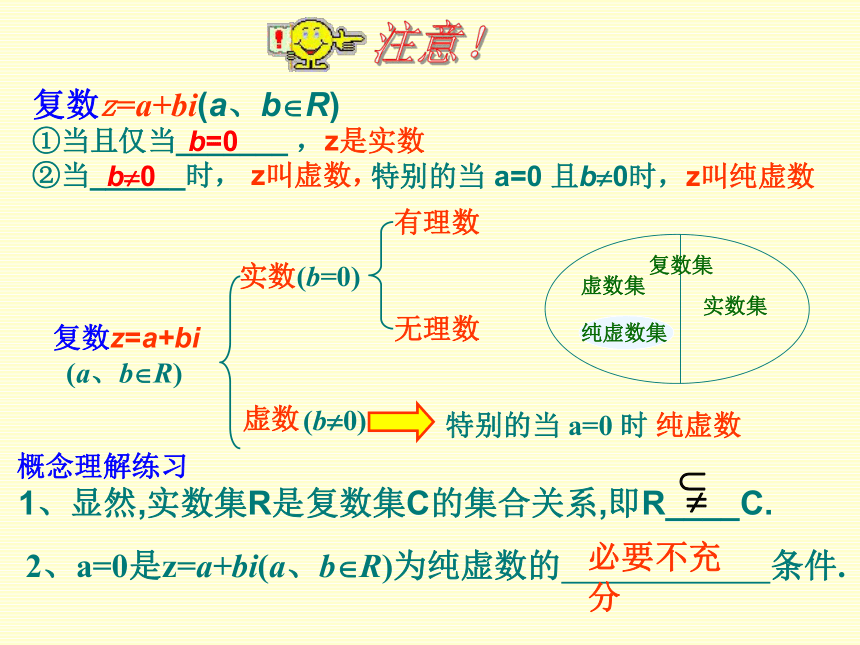
代数形式。复数z=a+bi(a、b?R)
①当且仅当_______ ,z是实数
②当______时, z叫虚数,(b=0)虚数(b?0)特别的当 a=0 时纯虚数2、a=0是z=a+bi(a、b?R)为纯虚数的 条件. 必要不充分注意! 概念理解练习
1、显然,实数集R是复数集C的集合关系,即R____C.b=0b?0特别的当 a=0 且b?0时,z叫纯虚数3练习:设集合C={复数},A={实数},B={纯虚数},若全集S=C,则下列结论正确的是( )
A. A∪B = C B.CSA = B
C. A∩(CSB) = D.B∪(CSB) = C数集扩充之后,常用的数集之间的关系如何?1 下列复数中,哪些是实数、哪些是虚数、哪些是纯虚数?例1、实数m取什么值时,复数Z=m+1+(m-1)i是
(1)实数?(2)虚数?(3)纯虚数?变式:已知复数Z=
试求实数a取什么值时,Z分别为 :
(1)实数?(2)虚数?(3)纯虚数?三 两个复数相等设z1=a+bi,z2=c+di(a、b、c、d?R),则 z1=z2? , 即实部等于实部,虚部等于虚部.特别地,a+bi=0? .a=b=0注意:一般地,两个复数只能说相等或不相等,而不能比较大小.思考3:对于任意的两个复数到底能否比较大小?答案:当且仅当两个复数都是实数时,才能比较大小.即:若z1>z2 z1,z2∈R且z1>z2.练习1、已知(x+y)+(x-2y)i=(2x-5)+(3x+y)i,求实数x,y的值.解:有两个复数相等的充要条件得:解得:x=3、y=-2例2 已知(x-2y-1)+(2x+y)i=-4+4i,求实数x,y的值练习2 方程2x2-3x-2+(x2-5x+6)i=0(x∈R),求x1. 由于i2= = -1,知i为-1的一个 、-1的另一个 ;一般地,a(a>0)的平方根为 、(-i)2平方根平方根为-i- a (a>0)的平方根为2、已知Z=m2(1+i)-(m+i),m为实数,当m为何值时,复数Z是
(1)实数 (2)虚数 (3)纯虚数通过本节课的学习,你掌握了那些知识?1.数的概念的发展及数系的扩充过程;
2.复数的有关概念;
3.复数相等的充要条件.
作业:习题3.1 - 1、22、已知关于x的方程x2+(1+2i)x-3mi+i=0有实根,求纯虚数
m的值.1、已知方程(1+i)x2-2(m+i)x+5-3i=0有实数解,m为实数,
求a的值.解:设方程的解为x0
来的,人类早在蒙昧时代就已具有识别事物多寡的
能力,从这种原始“数觉”到抽象的“数”概念的形成,
是一个缓慢的、渐进的过程。开始时用手指计数,
当手指不敷运用时,用小石子检查放牧归来的羊的
只数,出现了石子记数;用结绳的方法统计猎物的
个数,称为结绳记数;用在木头上刻道的方法记录
捕鱼的数量为刻痕记数等等。
为了记数的需要产生了自然数,为了测量产生了
分数,为了刻画相反意义的数产生了负数,为解决
度量正方形对角线长的问题出现了无理数。一 数系的扩充从数学内部来看,数集是在按某种“规则”不断扩充的。在
自然数集中,加法和乘法总可以实施。由于小数不能减大数,
要使x+4=0有解,从而引入_______.自然数集扩充到整数集;
在整数集中,加法、减法和乘法总可以实施。由于除法只能
解决整除问题,要使方程3x-2=0有解,为此引入________.
整数集扩充到有理数集;在有理数集里加、减、乘和除(除数
不为零)总可实施;要使x2-2=0有解,为此引入________,有
理数扩充到实数集。思考1:以上数系扩充的过程是___________________.每一次数的概念发展,都是在原来数集基础上“添加”一种新
的数得来在新的数集中,原来的运算和性质仍然使用。同时
解决了某些运算在原来数集中不是总可以实施的矛盾。无理数分数负数思考2:在实数集中,方程x2+1=0无解,为使方程x2+1=0有解
,实数集应怎样扩充呢?为此,我们引入一个新数 , 叫做虚数单位,并规定: (1)它的平方等于 -1,即新授课(2)实数可以与它进行四则运算,进行四则运算时,原有的加、乘运算律仍然成立. 二.复数的有关概念 复数z=a+bi(a, b∈R)由两部分组成,实数a与b分别称为复数a+bi的实部与虚部,1与i分别是实数单位和虚数单位 形如 a+bi (a,b∈R)的数叫做复数. 其中i 叫做虚数
单位,由全体复数组成的集合C={a+bi}叫做复数集.
说明:
复数常用字母z 表示,即z=a+bi (a,b∈R)叫复数的
代数形式。复数z=a+bi(a、b?R)
①当且仅当_______ ,z是实数
②当______时, z叫虚数,(b=0)虚数(b?0)特别的当 a=0 时纯虚数2、a=0是z=a+bi(a、b?R)为纯虚数的 条件. 必要不充分注意! 概念理解练习
1、显然,实数集R是复数集C的集合关系,即R____C.b=0b?0特别的当 a=0 且b?0时,z叫纯虚数3练习:设集合C={复数},A={实数},B={纯虚数},若全集S=C,则下列结论正确的是( )
A. A∪B = C B.CSA = B
C. A∩(CSB) = D.B∪(CSB) = C数集扩充之后,常用的数集之间的关系如何?1 下列复数中,哪些是实数、哪些是虚数、哪些是纯虚数?例1、实数m取什么值时,复数Z=m+1+(m-1)i是
(1)实数?(2)虚数?(3)纯虚数?变式:已知复数Z=
试求实数a取什么值时,Z分别为 :
(1)实数?(2)虚数?(3)纯虚数?三 两个复数相等设z1=a+bi,z2=c+di(a、b、c、d?R),则 z1=z2? , 即实部等于实部,虚部等于虚部.特别地,a+bi=0? .a=b=0注意:一般地,两个复数只能说相等或不相等,而不能比较大小.思考3:对于任意的两个复数到底能否比较大小?答案:当且仅当两个复数都是实数时,才能比较大小.即:若z1>z2 z1,z2∈R且z1>z2.练习1、已知(x+y)+(x-2y)i=(2x-5)+(3x+y)i,求实数x,y的值.解:有两个复数相等的充要条件得:解得:x=3、y=-2例2 已知(x-2y-1)+(2x+y)i=-4+4i,求实数x,y的值练习2 方程2x2-3x-2+(x2-5x+6)i=0(x∈R),求x1. 由于i2= = -1,知i为-1的一个 、-1的另一个 ;一般地,a(a>0)的平方根为 、(-i)2平方根平方根为-i- a (a>0)的平方根为2、已知Z=m2(1+i)-(m+i),m为实数,当m为何值时,复数Z是
(1)实数 (2)虚数 (3)纯虚数通过本节课的学习,你掌握了那些知识?1.数的概念的发展及数系的扩充过程;
2.复数的有关概念;
3.复数相等的充要条件.
作业:习题3.1 - 1、22、已知关于x的方程x2+(1+2i)x-3mi+i=0有实根,求纯虚数
m的值.1、已知方程(1+i)x2-2(m+i)x+5-3i=0有实数解,m为实数,
求a的值.解:设方程的解为x0
