3.2.1复数代数形式的加减运算及几何意义
文档属性
| 名称 | 3.2.1复数代数形式的加减运算及几何意义 |  | |
| 格式 | rar | ||
| 文件大小 | 129.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-05 22:34:00 | ||
图片预览







文档简介
课件27张PPT。3.2 复数的代数形式的四则运算3.2.1复数代数形式的加减运算及几何意义知识回顾1、复数的概念:形如______________的数叫做复数,a,b分别叫做它的_____________。
2、复数Z1=a1+b1i与Z2=a2+b2i 相等的充要条件是
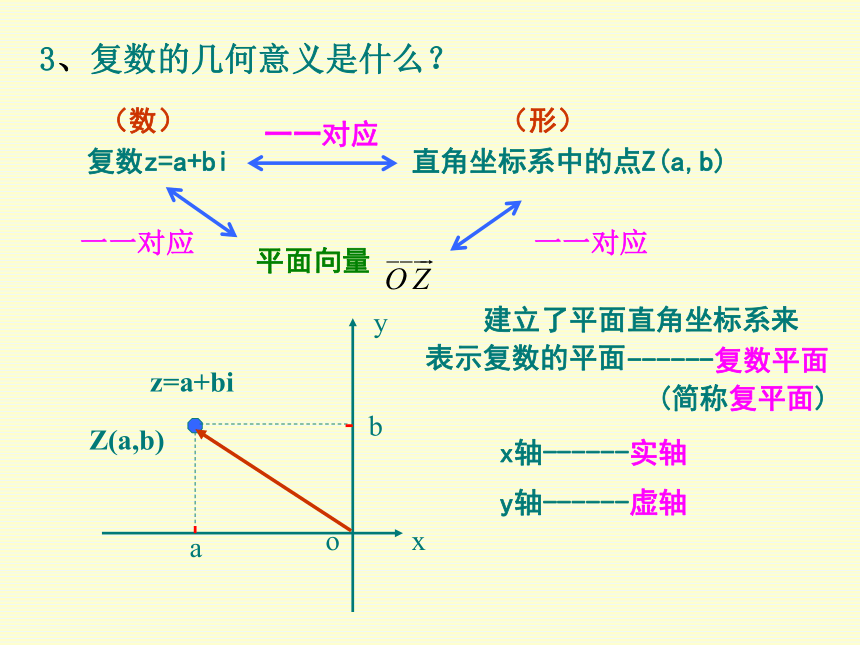
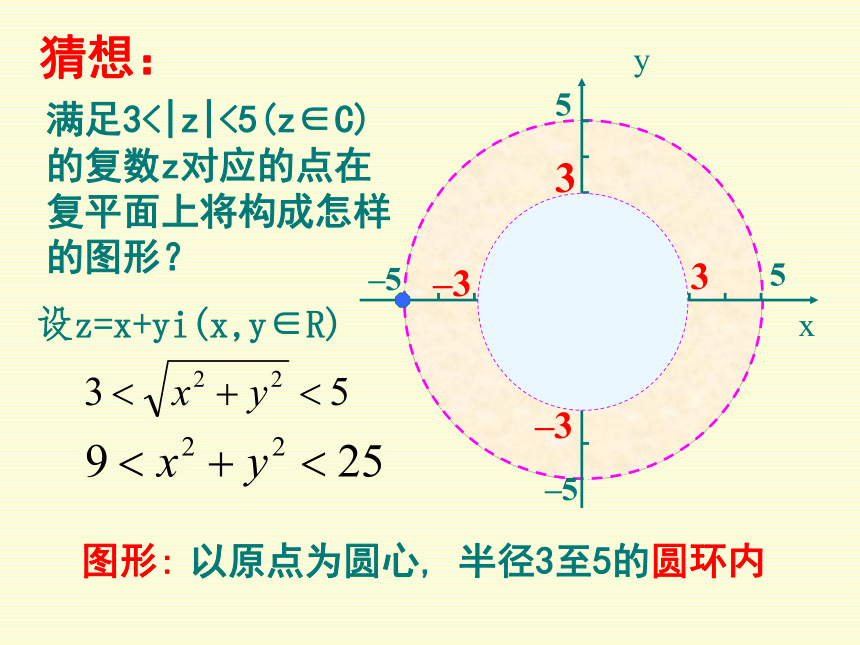
_____________。a1=a2,b1=b2a+bi(a,b∈R)实部和虚部3、复数的几何意义是什么?复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应xyobaZ(a,b)z=a+bix轴------实轴y轴------虚轴 建立了平面直角坐标系来表示复数的平面------复数平面 (简称复平面)(数)(形)3、复数的几何意义是什么?xOz=a+biyZ (a,b)对应平面向量 的模| |,即复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。| z | = 4、复数的绝对值(复数的模)的几何意义是什么?思考:(1)满足|z|=5(z∈R)的z值有几个? (2)这些复数对应的点在复平面上构成怎样的图形? xyO设z=x+yi(x,y∈R)满足|z|=5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–5图形:以原点为圆心,5为半径的圆上5xyO设z=x+yi(x,y∈R)满足3<|z|<5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–53–3–33图形:以原点为圆心, 半径3至5的圆环内猜想: 对一般的两个复数相加有什么猜想,即z1=a1+b1i, z2=a2+b2i ,z1+z2=? 问题猜想(a+bi)+(c+di)=(a+c)+(b+d)i我们规定复数的加法法则:点评:(1)复数的加法运算法则是一种规定。当b=0,
d=0时与实数加法法则保持一致。 (2)两个复数的和仍然是一个复数。对于复数的加法可以推广到多个复数相加的情形。点评:实数加法运算的交换律、结合律在复数集C中依然成立。设问1:复数的加法满足交换律,结合律吗?
即:对于任意的 ,有则Z1+Z2=(a1+a2)+(b1+b2)i,
Z2+Z1=(a2+a1)+(b2+b1)i证:设Z1=a1+b1i,Z2=a2+b2i,Z3=a3+b3i (a1,a2,a3,b1,b2,b3∈R)类比猜想设问2、类比复数的加法法则,你认为复数有减法吗?复数的减法法则如何呢?复数的减法规定是加法的逆运算,即把满足 (c+di)+(x+yi)= a+bi的复数x+yi 叫做复数a+bi减去复数c+di的差,记作(a+bi)-(c+di)(a+bi)-(c+di)=(a-c)+(b-d)i点评:根据复数相等的定义,我们可以得出复数的减法法则,且知两个复数的差是唯一确定的复数。复数的减法法则:即:两个复数相加(减)就是实部与实部,虚部与虚部分别相加(减).结果还是一个复数。
归纳总结一、复数加法与减法的运算法则例1、计算(5-6i )+(-2-i) - (3+4i)= -11i .例题讲解点评:复数可以求和差,虚实各自相加减练习:计算下列各式⑴ (2+4i)+(3-4i)
⑵ (-3+2i)-(-3-2i)
⑶ (4-i)+3i
⑷ 5-(3+2i)
⑸ (-3-4i)+(2+i)-(1-5i)
⑹ (2-i)-(2+3i)+4i学以致用复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应xyobaZ(a,b)z=a+bi二、复数加法与减法运算的几何意义?由此出发探讨复数加法的几何意义xoyZ1(a,b)Z2(c,d)Z(a+c,b+d)z1+ z2=OZ1 +OZ2 = OZ符合向量加法的平行四边形法则.1.复数加法运算的几何意义?问题探索xoyZ1(a,b)Z2(c,d)符合向量减法的三角形法则.2.复数减法运算的几何意义?问题探索二、复数加法与减法运算的几何意义 复数的和对应向量的和 复数的差对应向量的差归纳总结练习、如图的向量 对应复数z,试作出下列运算的结果对应的向量 xyo1z几何意义运用例3 已知 求向量 对应的复数.
变式1 已知复平面内一平行四边形AOBC顶点A,O,B对应复数是 -3+2i, 0, 2+i ,求点C对应的复数.
几何意义运用变式1 已知复平面内一平行四边形AOBC顶点A,O,B对应复数是 -3+2i, 0, 2+i ,求点C对应的复数.解:复数-3+2i ,2+i,0对应点A(-3,2),B(2,1),O(0,0),如图. ∴ 点C对应的复数是-1+3i 在平行四边形 AOBC中,xyA 0CB几何意义运用第四个顶点对应的复数是6+4i,-4+6i,-2-i变式2 已知复平面内一平行四边形三个顶点A,B,C对应复数分别是-3+2i, 2+i, 1+5i求第四个对应的复数.XyxoyZ1(a,b)Z2(c,d)复数z2-z1符合向量减法的三角形法则.2.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1 ,Z2的距离拓展延伸复平面内两点间距离复平面内两点距离就是对应两个复数的差的模转化推广(1)|z-(1+2i)|(2)|z+(1+2i)| 已知复数z对应点A,说明下列各式所表示的几何意义.点A到点(1,2)的距离点A到点(-1, -2)的距离(3)|z-1|(4)|z+2i|点A到点(1,0)的距离点A到点(0, -2)的距离复数加减复平面的点坐标运算一一对应一一对应一一对应平面向量加减1.复数代数形式的加减运算:
复数可以求和差,虚实各自相加减。2.复数加减运算的几何意义:课堂小结1)教材P63习题3.2 A组ex1~3
2)类比实数的乘法和除法,试探讨复数的乘除法运算。
3)预习3.2.2复数代数形式的乘除运算。反馈作业再见!
2、复数Z1=a1+b1i与Z2=a2+b2i 相等的充要条件是
_____________。a1=a2,b1=b2a+bi(a,b∈R)实部和虚部3、复数的几何意义是什么?复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应xyobaZ(a,b)z=a+bix轴------实轴y轴------虚轴 建立了平面直角坐标系来表示复数的平面------复数平面 (简称复平面)(数)(形)3、复数的几何意义是什么?xOz=a+biyZ (a,b)对应平面向量 的模| |,即复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。| z | = 4、复数的绝对值(复数的模)的几何意义是什么?思考:(1)满足|z|=5(z∈R)的z值有几个? (2)这些复数对应的点在复平面上构成怎样的图形? xyO设z=x+yi(x,y∈R)满足|z|=5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–5图形:以原点为圆心,5为半径的圆上5xyO设z=x+yi(x,y∈R)满足3<|z|<5(z∈C)的复数z对应的点在复平面上将构成怎样的图形?55–5–53–3–33图形:以原点为圆心, 半径3至5的圆环内猜想: 对一般的两个复数相加有什么猜想,即z1=a1+b1i, z2=a2+b2i ,z1+z2=? 问题猜想(a+bi)+(c+di)=(a+c)+(b+d)i我们规定复数的加法法则:点评:(1)复数的加法运算法则是一种规定。当b=0,
d=0时与实数加法法则保持一致。 (2)两个复数的和仍然是一个复数。对于复数的加法可以推广到多个复数相加的情形。点评:实数加法运算的交换律、结合律在复数集C中依然成立。设问1:复数的加法满足交换律,结合律吗?
即:对于任意的 ,有则Z1+Z2=(a1+a2)+(b1+b2)i,
Z2+Z1=(a2+a1)+(b2+b1)i证:设Z1=a1+b1i,Z2=a2+b2i,Z3=a3+b3i (a1,a2,a3,b1,b2,b3∈R)类比猜想设问2、类比复数的加法法则,你认为复数有减法吗?复数的减法法则如何呢?复数的减法规定是加法的逆运算,即把满足 (c+di)+(x+yi)= a+bi的复数x+yi 叫做复数a+bi减去复数c+di的差,记作(a+bi)-(c+di)(a+bi)-(c+di)=(a-c)+(b-d)i点评:根据复数相等的定义,我们可以得出复数的减法法则,且知两个复数的差是唯一确定的复数。复数的减法法则:即:两个复数相加(减)就是实部与实部,虚部与虚部分别相加(减).结果还是一个复数。
归纳总结一、复数加法与减法的运算法则例1、计算(5-6i )+(-2-i) - (3+4i)= -11i .例题讲解点评:复数可以求和差,虚实各自相加减练习:计算下列各式⑴ (2+4i)+(3-4i)
⑵ (-3+2i)-(-3-2i)
⑶ (4-i)+3i
⑷ 5-(3+2i)
⑸ (-3-4i)+(2+i)-(1-5i)
⑹ (2-i)-(2+3i)+4i学以致用复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应xyobaZ(a,b)z=a+bi二、复数加法与减法运算的几何意义?由此出发探讨复数加法的几何意义xoyZ1(a,b)Z2(c,d)Z(a+c,b+d)z1+ z2=OZ1 +OZ2 = OZ符合向量加法的平行四边形法则.1.复数加法运算的几何意义?问题探索xoyZ1(a,b)Z2(c,d)符合向量减法的三角形法则.2.复数减法运算的几何意义?问题探索二、复数加法与减法运算的几何意义 复数的和对应向量的和 复数的差对应向量的差归纳总结练习、如图的向量 对应复数z,试作出下列运算的结果对应的向量 xyo1z几何意义运用例3 已知 求向量 对应的复数.
变式1 已知复平面内一平行四边形AOBC顶点A,O,B对应复数是 -3+2i, 0, 2+i ,求点C对应的复数.
几何意义运用变式1 已知复平面内一平行四边形AOBC顶点A,O,B对应复数是 -3+2i, 0, 2+i ,求点C对应的复数.解:复数-3+2i ,2+i,0对应点A(-3,2),B(2,1),O(0,0),如图. ∴ 点C对应的复数是-1+3i 在平行四边形 AOBC中,xyA 0CB几何意义运用第四个顶点对应的复数是6+4i,-4+6i,-2-i变式2 已知复平面内一平行四边形三个顶点A,B,C对应复数分别是-3+2i, 2+i, 1+5i求第四个对应的复数.XyxoyZ1(a,b)Z2(c,d)复数z2-z1符合向量减法的三角形法则.2.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1 ,Z2的距离拓展延伸复平面内两点间距离复平面内两点距离就是对应两个复数的差的模转化推广(1)|z-(1+2i)|(2)|z+(1+2i)| 已知复数z对应点A,说明下列各式所表示的几何意义.点A到点(1,2)的距离点A到点(-1, -2)的距离(3)|z-1|(4)|z+2i|点A到点(1,0)的距离点A到点(0, -2)的距离复数加减复平面的点坐标运算一一对应一一对应一一对应平面向量加减1.复数代数形式的加减运算:
复数可以求和差,虚实各自相加减。2.复数加减运算的几何意义:课堂小结1)教材P63习题3.2 A组ex1~3
2)类比实数的乘法和除法,试探讨复数的乘除法运算。
3)预习3.2.2复数代数形式的乘除运算。反馈作业再见!
