2.1函数的概念及其表示方法
图片预览







文档简介
课件27张PPT。2.1函数的概念及其表示方法要点·疑点·考点1.映射
设A,B是两个非空集合,如果按照某种对应法则f,对于集合A中的任何一个元素,在集合B中都有惟一的元素和它对应,那么这样的对应叫做集合A到集合B的映射,记作f:A→B .给定一个集合A到B的映射,且a∈A,b∈B.如果元素a和元素b对应,那么,我们把元素b叫做元素a的象,元素a叫做元素b的原象
设f:A→B是集合A到集合B的一个映射.如果在这个映射下,对于集合A中的不同元素,在集合B中有不同的象,而且B中每一个元素都有原象,那么这个映射就叫做A到B上的一一映射.
(1) 映射三要素: 原象、象、对应法则;
(2) 取元任意性,成象唯一性;(3) A中元素不可剩,B中元素可剩;即:多对一行,一对多不行;(4) 映射具有方向性:f : A→B与
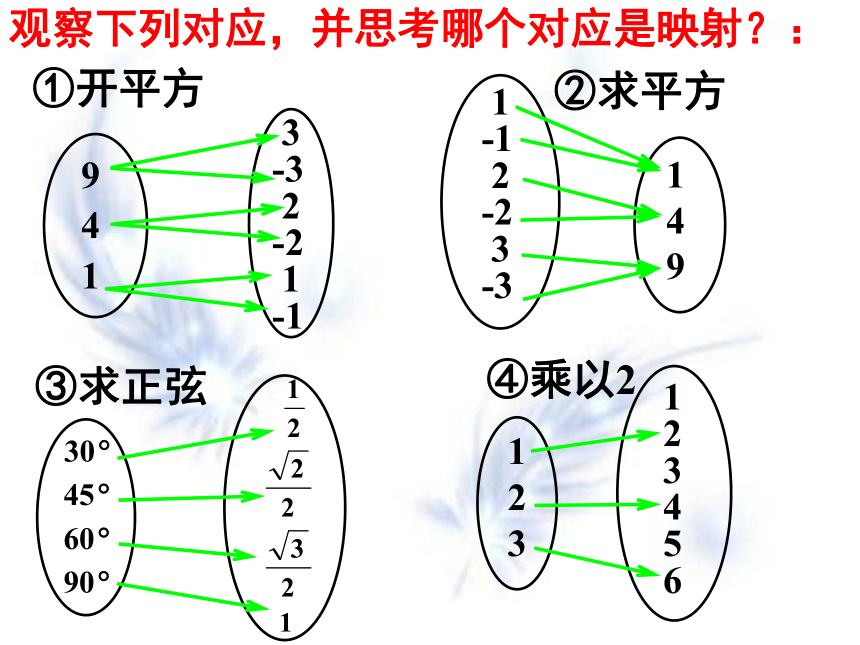
f : B→A是不同的映射;(5) 原象的集合为A, 象集C?B.说明:①开平方③求正弦 ④乘以2 1
-1
2
-2
3
-31
4
9②求平方 观察下列对应,并思考哪个对应是映射?:一种对应是映射,必须满足两个条件: ①A中任何一个元素在B中都有元素与之
对应(至于B中元素是否在A中有元素对应
不必考虑,即B中可有“多余”元素). ②B中所对应的元素是唯一的 (即“一对
多”不是映射,而“多对一”可构成映
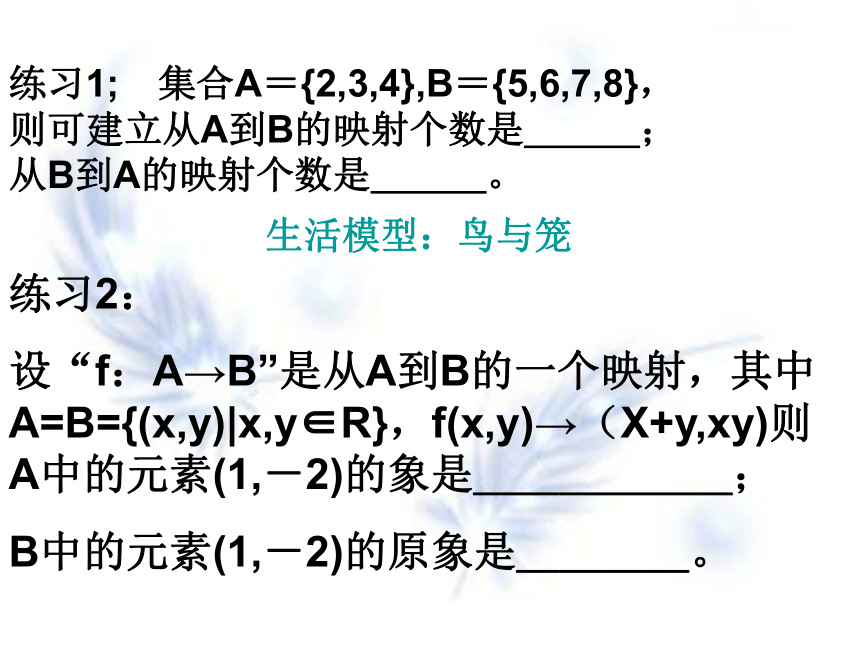
射,如图(1)中对应不是映射).理 解:练习1; 集合A={2,3,4},B={5,6,7,8},则可建立从A到B的映射个数是___;从B到A的映射个数是___。生活模型:鸟与笼练习2:
设“f:A→B”是从A到B的一个映射,其中A=B={(x,y)|x,y∈R},f(x,y)→(X+y,xy)则A中的元素(1,-2)的象是______;
B中的元素(1,-2)的原象是____。初中已经学过:正比例函数、反比例函数、
一次函数、二次函数等。 设在一个变化过程中有两个变量x和y,如果对于x
的每一个值,y都有唯一的值与它对应,那么就说
x是自变量,y是x的函数.并将自变量x取值的集合
叫做函数的定义域,和自变量x的值对应的y值叫
做函数值,函数值的集合叫做函数的值域.这种用
变量叙述的函数定义我们称之为函数的传统定义.二 函数的概念1 传统定义2 近代定义 定义:设A、B是非空的数集,如果按照某种确定的对
应关系f,使对于集合A中的任意一个数x,在集合B中
都有唯一确定的数f(x)和它对应,那么就称
f: A→B为从集合A到集合B的一个函数(fun_ction),
记作y=f (x),x∈A。定义域(domain):x的取值范围A叫做函数的定义域;
与x值相对应的y值叫做函数值。
值域(range):函数值的集合叫做函数的值域。函数概念理解应注意的问题
(1)函数是一种特殊的映射,f:A→B必须满足A、B都是非空数集,其象的集合是B的子集.(2)构成函数的三要素是:定义域、值域和对应法则,而值域由定义域和对应法则可以确定.分析判断两函数是否为同一函数时,就从这三个方面进行分析,只有三者完全相同时才为同一个函数.(3)不同的函数,会有不同的对应法则,如y=f(x)=sinx,其对应法则为“取正弦”.练习:以下四组函数中,表示同一函数的是
A.f(x)=x-1,g(x)=(x2-1)/(x+1)
B.f(x)=x-1,
C.f(x)=x-1,
D.f(x)=(x-1)0,g(x)=(x―1)/(x―1)1.判断对应是否为映射,即看A中元素是否满足“每元有象”和“象唯一”,即可以是“一对一”或者“多对一”.
2.f:A→B形成函数时,A即函数的定义域,但B不一定是值域.如果B中的元素都有原象,则B才是值域,即函数就是从定义域到值域的映射.课堂互动讲练已知函数f(x),g(x)分别由下表给出
则f[g(1)]的值为________;满足f[g(x)]>g[f(x)]的x的值是________.【思路点拨】 由表格的映射可看出f(1)=f(3)=1,
f(2)=3,g(1)=3,g(2)=2,g(3)=1,可解决问题.【解析】 ∵g(1)=3,∴f[g(1)]=f(3)=1.
当x=1时,g(1)=3,f(3)=1,
而f(1)=1,g(1)=3,不适合f[g(x)]>g[f(x)],
同理可验证x=2,3时f[g(x)]与g[f(x)]的大小关系,当x=2时不等式成立.
【答案】 1 2基础知识梳理思考?映射与函数有什么区别?
【思考·提示】 函数是特殊的映射,二者区别在于映射定义中的两个集合是非空集合,可以不是数集,而函数中的两个集合必须是非空数集. 解析法
列表法
图象法三 函数的表示法: 把两个变量的关系, 用一个等式
表示, 这个等式就叫做函数的解析式.1. 解析法:函数的表示法用解析式表示函数关系的优点是:函数关系清楚,容易根据自变量的值求出对应的函数值,便于用解析式来研究函数的性质.2. 列表法:优点:不必通过计算就知道自变量取某些值时函数的对应值.
列出表格来表示两个变量的关系.如:平方表,平方根表,汽车、
火车站的里程价目表、银行里的
“利率表”等等. 优点:直观形象表示出函数值的变化情况. 3. 图象法:如:一次函数的图象是一条直线;
如函数 y=kx+b (k<0、b>0) 用函数图象来表示两个变量之
间的关系.课堂互动讲练已知某人在2009年1月份至6月份的月经济收入如下:1月份为1000元,从2月份起每月的月经济收入是其上一个月的2倍,用列表、图象、解析式三种不同形式来表示该人1月份至6月份的月经济收入y(元)与月份序号x的函数关系,并指出该函数的定义域、值域和对应法则.【思路点拨】 月份为自变量,月工资为函数值.【解】 列表:课堂互动讲练图象:解析式:y=1000·2x-1(x∈{1,2,3,4,5,6}).
其中定义域为{1,2,3,4,5,6},值域为{1000,2000,4000,8000,16000,32000}.
对应法则f:x→y=1000·2x-1.
【规律小结】 列表法、图象法和解析式法是表示函数的三种方法,其实质是一样的,只是形式上的区别,列表和图象更加直观,解析式更适合计算和应用.在对待不同题目时,选择不同的表示方法,因为有的函数根本写不出其解析式.课堂互动讲练练习: 2.已知34.5求f(x+1)
3.设函数 ,
则x0的取值范围是( )
(A)(-1,1) (B)(-1,+∞)
(C)(-∞,-2)∪(0,+∞) (D)(-∞,-1)∪(1,+∞)D小结2.函数的三要素定义域A值域B对应法则f定义域对应法则值域1函数的概念:设A、B是非空数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有惟一确定的数f(x)和它对应,那么就称f:A B为从集合A到集合 B的函数.五 复合函数如果y=f(u),u=g(x),那么,y=f[g(x)]叫做f和g的复合函数,其中, g(x)叫内层函数,f(u)为外层函数 函数
对应映射函数情,约束条件渐渐增。
任一原象唯一象,分段函数段段清。
设A,B是两个非空集合,如果按照某种对应法则f,对于集合A中的任何一个元素,在集合B中都有惟一的元素和它对应,那么这样的对应叫做集合A到集合B的映射,记作f:A→B .给定一个集合A到B的映射,且a∈A,b∈B.如果元素a和元素b对应,那么,我们把元素b叫做元素a的象,元素a叫做元素b的原象
设f:A→B是集合A到集合B的一个映射.如果在这个映射下,对于集合A中的不同元素,在集合B中有不同的象,而且B中每一个元素都有原象,那么这个映射就叫做A到B上的一一映射.
(1) 映射三要素: 原象、象、对应法则;
(2) 取元任意性,成象唯一性;(3) A中元素不可剩,B中元素可剩;即:多对一行,一对多不行;(4) 映射具有方向性:f : A→B与
f : B→A是不同的映射;(5) 原象的集合为A, 象集C?B.说明:①开平方③求正弦 ④乘以2 1
-1
2
-2
3
-31
4
9②求平方 观察下列对应,并思考哪个对应是映射?:一种对应是映射,必须满足两个条件: ①A中任何一个元素在B中都有元素与之
对应(至于B中元素是否在A中有元素对应
不必考虑,即B中可有“多余”元素). ②B中所对应的元素是唯一的 (即“一对
多”不是映射,而“多对一”可构成映
射,如图(1)中对应不是映射).理 解:练习1; 集合A={2,3,4},B={5,6,7,8},则可建立从A到B的映射个数是___;从B到A的映射个数是___。生活模型:鸟与笼练习2:
设“f:A→B”是从A到B的一个映射,其中A=B={(x,y)|x,y∈R},f(x,y)→(X+y,xy)则A中的元素(1,-2)的象是______;
B中的元素(1,-2)的原象是____。初中已经学过:正比例函数、反比例函数、
一次函数、二次函数等。 设在一个变化过程中有两个变量x和y,如果对于x
的每一个值,y都有唯一的值与它对应,那么就说
x是自变量,y是x的函数.并将自变量x取值的集合
叫做函数的定义域,和自变量x的值对应的y值叫
做函数值,函数值的集合叫做函数的值域.这种用
变量叙述的函数定义我们称之为函数的传统定义.二 函数的概念1 传统定义2 近代定义 定义:设A、B是非空的数集,如果按照某种确定的对
应关系f,使对于集合A中的任意一个数x,在集合B中
都有唯一确定的数f(x)和它对应,那么就称
f: A→B为从集合A到集合B的一个函数(fun_ction),
记作y=f (x),x∈A。定义域(domain):x的取值范围A叫做函数的定义域;
与x值相对应的y值叫做函数值。
值域(range):函数值的集合叫做函数的值域。函数概念理解应注意的问题
(1)函数是一种特殊的映射,f:A→B必须满足A、B都是非空数集,其象的集合是B的子集.(2)构成函数的三要素是:定义域、值域和对应法则,而值域由定义域和对应法则可以确定.分析判断两函数是否为同一函数时,就从这三个方面进行分析,只有三者完全相同时才为同一个函数.(3)不同的函数,会有不同的对应法则,如y=f(x)=sinx,其对应法则为“取正弦”.练习:以下四组函数中,表示同一函数的是
A.f(x)=x-1,g(x)=(x2-1)/(x+1)
B.f(x)=x-1,
C.f(x)=x-1,
D.f(x)=(x-1)0,g(x)=(x―1)/(x―1)1.判断对应是否为映射,即看A中元素是否满足“每元有象”和“象唯一”,即可以是“一对一”或者“多对一”.
2.f:A→B形成函数时,A即函数的定义域,但B不一定是值域.如果B中的元素都有原象,则B才是值域,即函数就是从定义域到值域的映射.课堂互动讲练已知函数f(x),g(x)分别由下表给出
则f[g(1)]的值为________;满足f[g(x)]>g[f(x)]的x的值是________.【思路点拨】 由表格的映射可看出f(1)=f(3)=1,
f(2)=3,g(1)=3,g(2)=2,g(3)=1,可解决问题.【解析】 ∵g(1)=3,∴f[g(1)]=f(3)=1.
当x=1时,g(1)=3,f(3)=1,
而f(1)=1,g(1)=3,不适合f[g(x)]>g[f(x)],
同理可验证x=2,3时f[g(x)]与g[f(x)]的大小关系,当x=2时不等式成立.
【答案】 1 2基础知识梳理思考?映射与函数有什么区别?
【思考·提示】 函数是特殊的映射,二者区别在于映射定义中的两个集合是非空集合,可以不是数集,而函数中的两个集合必须是非空数集. 解析法
列表法
图象法三 函数的表示法: 把两个变量的关系, 用一个等式
表示, 这个等式就叫做函数的解析式.1. 解析法:函数的表示法用解析式表示函数关系的优点是:函数关系清楚,容易根据自变量的值求出对应的函数值,便于用解析式来研究函数的性质.2. 列表法:优点:不必通过计算就知道自变量取某些值时函数的对应值.
列出表格来表示两个变量的关系.如:平方表,平方根表,汽车、
火车站的里程价目表、银行里的
“利率表”等等. 优点:直观形象表示出函数值的变化情况. 3. 图象法:如:一次函数的图象是一条直线;
如函数 y=kx+b (k<0、b>0) 用函数图象来表示两个变量之
间的关系.课堂互动讲练已知某人在2009年1月份至6月份的月经济收入如下:1月份为1000元,从2月份起每月的月经济收入是其上一个月的2倍,用列表、图象、解析式三种不同形式来表示该人1月份至6月份的月经济收入y(元)与月份序号x的函数关系,并指出该函数的定义域、值域和对应法则.【思路点拨】 月份为自变量,月工资为函数值.【解】 列表:课堂互动讲练图象:解析式:y=1000·2x-1(x∈{1,2,3,4,5,6}).
其中定义域为{1,2,3,4,5,6},值域为{1000,2000,4000,8000,16000,32000}.
对应法则f:x→y=1000·2x-1.
【规律小结】 列表法、图象法和解析式法是表示函数的三种方法,其实质是一样的,只是形式上的区别,列表和图象更加直观,解析式更适合计算和应用.在对待不同题目时,选择不同的表示方法,因为有的函数根本写不出其解析式.课堂互动讲练练习: 2.已知34.5求f(x+1)
3.设函数 ,
则x0的取值范围是( )
(A)(-1,1) (B)(-1,+∞)
(C)(-∞,-2)∪(0,+∞) (D)(-∞,-1)∪(1,+∞)D小结2.函数的三要素定义域A值域B对应法则f定义域对应法则值域1函数的概念:设A、B是非空数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有惟一确定的数f(x)和它对应,那么就称f:A B为从集合A到集合 B的函数.五 复合函数如果y=f(u),u=g(x),那么,y=f[g(x)]叫做f和g的复合函数,其中, g(x)叫内层函数,f(u)为外层函数 函数
对应映射函数情,约束条件渐渐增。
任一原象唯一象,分段函数段段清。
