《第二章 点、线、面之间的位置关系》习题一
文档属性
| 名称 | 《第二章 点、线、面之间的位置关系》习题一 |  | |
| 格式 | zip | ||
| 文件大小 | 42.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-06 09:52:00 | ||
图片预览

文档简介
课题:《第二章 点、线、面之间的位置关系》习题课一
高一数学教案40 设计人:唐桂荣 设计时间:5.5 授课时间: 组长签字:
一、教学目标
1.知识与能力:
(1)使学生掌握知识结构与联系,进一步巩固、深化所学知识;
(2)通过对知识的梳理,提高学生的归纳知识和综合运用知识的能力。
2.过程与方法:利用框图对本章知识进行系统的小结,直观、简明再现所学知识,化抽象学习为直观学习,易于识记;同时凸现数学知识的发展和联系。
3.态度与价值观:学生通过知识的整合、梳理,理会空间点、线面间的位置关系及其互相联系,进一步培养学生的空间想象能力和解决问题能力。
二、教学重点:知识点间的网络关系;
教学难点:在空间如何实现平行关系、垂直关系、垂直与平行关系之间的转化。
三、学法指导: 启发、引导、归纳、分类等
四、知识链接:(一)知识回顾,整体认识:
1、本章知识回顾
(1)空间点、线、面间的位置关系;
(2)直线、平面平行的判定及性质;
(3)直线、平面垂直的判定及性质。
2、本章知识结构框图:
(二)整合知识,发展思维
1、刻画平面的三个公理是立体几何公理体系的基石,是研究空间图形问题,进行逻辑推理的基础。
公理1——判定直线是否在平面内的依据;公理2——提供确定平面最基本的依据;
公理3——判定两个平面交线位置的依据;公理4——判定空间直线之间平行的依据。
2、空间问题解决的重要思想方法:化空间问题为平面问题;
3、空间平行、垂直之间的转化与联系:
【注】 :以上模块大约用时2-3分钟
五、学习过程:(本模块大约用时5-7分钟)
A1:下面四个命题:①分别在两个平面内的直线平行;②若两个平面平行,则其中一个平面内的任何一条直线必平行于另一个平面;③如果一个平面内的两条直线平行于另一个平面,则这两个平面平行;④如果一个平面内的任何一条直线都平行于另一个平面,则这两个平面平行.其中正确的命题是 : ( B )
A. ①② B. ②④ C. ①③ D. ②③
A2:设正方体的全面积为24,一个球内切于正方体,那么这个球的体积是 : ( D )
A. B. C. D.
A3:若三个平面两两相交,有三条交线,则下列命题中正确的是: ( D )
A. 三条交线为异面直线 B. 三条交线两两平行
C. 三条交线交与一点 D. 三条交线两两平行或交与一点
B4:菱形ABCD在平面内,,则PA与对角线BD的位置关系是 : ( D )
A.平行 B.相交但不垂直 C.垂直相交 D.异面垂直
六、当堂检测:(本模块大约用时25-27分钟)
B5:在正三棱柱ABC-中,若AB=,则与所成的角的大小为 : ( B )
A. B. C. D.
B6:设m、n是两条不同的直线,、是两个不同的平面,下列命题中正确的命题是:( B )
A. B.
C. D.
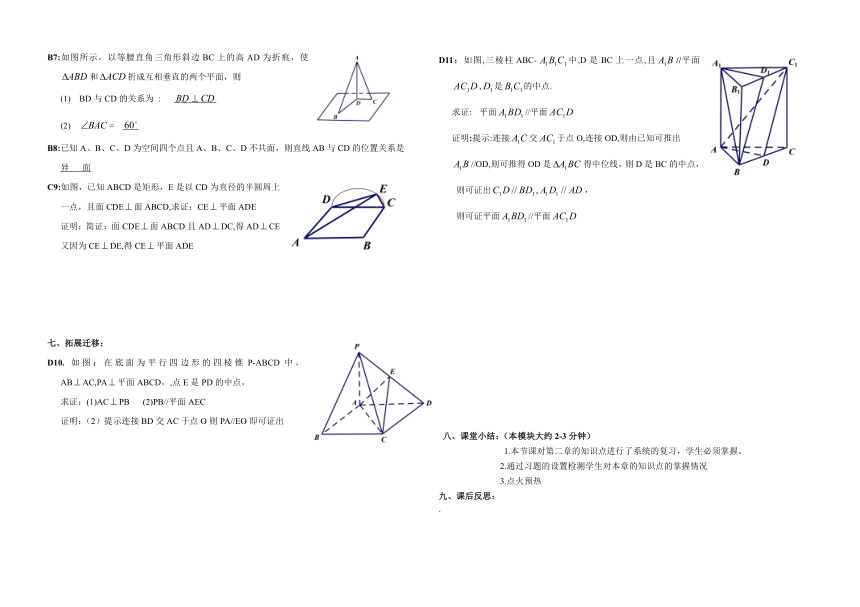
B7:如图所示,以等腰直角三角形斜边BC上的高AD为折痕,使 和折成互相垂直的两个平面,则
(1) BD与CD的关系为 :
(2) =
B8:已知A、B、C、D为空间四个点且A、B、C、D不共面,则直线AB与CD的位置关系是
异 面
C9:如图,已知ABCD是矩形,E是以CD为直径的半圆周上一点,且面CDE面ABCD,求证:CE平面ADE
证明:简证:面CDE面ABCD且ADDC,得ADCE又因为CEDE,得CE平面ADE
七、拓展迁移:
D10. 如图:在底面为平行四边形的四棱锥P-ABCD中,ABAC,PA平面ABCD,,点E是PD的中点,
求证:(1)ACPB (2)PB//平面AEC
证明:(2)提示连接BD交AC于点O则PA//EO即可证出
D11:如图,三棱柱ABC-中,D是BC上一点,且//平面,是的中点.
求证:平面//平面
证明:提示:连接交于点O,连接OD,则由已知可推出
//OD,则可推得OD是得中位线,则D是BC的中点,
则可证出,
则可证平面//平面
八、课堂小结:(本模块大约2-3分钟)
1.本节课对第二章的知识点进行了系统的复习,学生必须掌握。
2.通过习题的设置检测学生对本章的知识点的掌握情况
3.点火预热
九、课后反思:
.
课题:《第二章 点、线、面之间的位置关系》习题课一
高一数学学案40 设计人:唐桂荣 设计时间:5.5 授课时间: 组长签字:
一、学习目标
1.知识与能力:
(1)使学生掌握知识结构与联系,进一步巩固、深化所学知识;
(2)通过对知识的梳理,提高学生的归纳知识和综合运用知识的能力。
2.过程与方法:利用框图对本章知识进行系统的小结,直观、简明再现所学知识,化抽象学习为直观学习,易于识记;同时凸现数学知识的发展和联系。
3.态度与价值观:学生通过知识的整合、梳理,理会空间点、线面间的位置关系及其互相联系,进一步培养学生的空间想象能力和解决问题能力。
二、学习重点:知识点间的网络关系;
学习难点:在空间如何实现平行关系、垂直关系、垂直与平行关系之间的转化。
三、学法指导: 启发、引导、归纳、分类等
四、知识链接:(一)知识回顾,整体认识:
1、本章知识回顾
(1)空间点、线、面间的位置关系;
(2)直线、平面平行的判定及性质;
(3)直线、平面垂直的判定及性质。
2、本章知识结构框图:
(二)整合知识,发展思维
1、刻画平面的三个公理是立体几何公理体系的基石,是研究空间图形问题,进行逻辑推理的基础。
公理1——判定直线是否在平面内的依据;公理2——提供确定平面最基本的依据;
公理3——判定两个平面交线位置的依据;公理4——判定空间直线之间平行的依据。
2、空间问题解决的重要思想方法:化空间问题为平面问题;
3、空间平行、垂直之间的转化与联系:
【注】 :以上模块大约用时2-3分钟
高一( ) 班 . 第 ( )小组 . 姓名:
五、学习过程:(本模块大约用时5-7分钟)
A1:下面四个命题:①分别在两个平面内的直线平行;②若两个平面平行,则其中一个平面内的任何一条直线必平行于另一个平面;③如果一个平面内的两条直线平行于另一个平面,则这两个平面平行;④如果一个平面内的任何一条直线都平行于另一个平面,则这两个平面平行.其中正确的命题是 : ( )
A. ①② B. ②④ C. ①③ D. ②③
A2:设正方体的全面积为24,一个球内切于正方体,那么这个球的体积是 : ( )
A. B. C. D.
A3:若三个平面两两相交,有三条交线,则下列命题中正确的是: ( )
A. 三条交线为异面直线 B. 三条交线两两平行
C. 三条交线交与一点 D. 三条交线两两平行或交与一点
B4:菱形ABCD在平面内,,则PA与对角线BD的位置关系是 : ( )
A.平行 B.相交但不垂直 C.垂直相交 D.异面垂直
六、当堂检测:(本模块大约用时25-27分钟)
B5:在正三棱柱ABC-中,若AB=,则与所成的角的大小为 : ( )
A. B. C. D.
B6:设m、n是两条不同的直线,、是两个不同的平面,下列命题中正确的命题是:( )
A. B.
C. D.
B7:如图所示,以等腰直角三角形斜边BC上的高AD为折痕,使 和折成互相垂直的两个平面,则
(1) BD与CD的关系为
(2) =
B8:已知A、B、C、D为空间四个点且A、B、C、D不共面,
则直线AB与CD的位置关系是
C9:如图,已知ABCD是矩形,E是以CD为直径的半圆周上一点,且面CDE面ABCD,
求证:CE平面ADE
七、拓展迁移:
D10. 如图:在底面为平行四边形的四棱锥P-ABCD中, ABAC,PA平面ABCD,,点E是PD的中点,
求证:(1)ACPB (2)PB//平面AEC
D11:如图,三棱柱ABC-中,D是BC上一点,且//平面,是的中点.
求证:平面//平面
.
批改时间:第一次:2010年5 月 日 等级: 第二次:2010年5月 日
寄语: 只要再多一点努力,你就会多一点成功.
平面(公理1、公理2、公理3、公理4)
空间直线、平面的位置关系
直线与直线的位置关系
直线与平面的位置关系
平面与平面的位置关系
平面与平面平行
直线与直线平行
直线与平面平行
直线与平面垂直
平面与平面垂直
直线与直线垂直
平面(公理1、公理2、公理3、公理4)
空间直线、平面的位置关系
直线与直线的位置关系
直线与平面的位置关系
平面与平面的位置关系
平面与平面平行
直线与直线平行
直线与平面平行
直线与平面垂直
平面与平面垂直
直线与直线垂直
高一数学教案40 设计人:唐桂荣 设计时间:5.5 授课时间: 组长签字:
一、教学目标
1.知识与能力:
(1)使学生掌握知识结构与联系,进一步巩固、深化所学知识;
(2)通过对知识的梳理,提高学生的归纳知识和综合运用知识的能力。
2.过程与方法:利用框图对本章知识进行系统的小结,直观、简明再现所学知识,化抽象学习为直观学习,易于识记;同时凸现数学知识的发展和联系。
3.态度与价值观:学生通过知识的整合、梳理,理会空间点、线面间的位置关系及其互相联系,进一步培养学生的空间想象能力和解决问题能力。
二、教学重点:知识点间的网络关系;
教学难点:在空间如何实现平行关系、垂直关系、垂直与平行关系之间的转化。
三、学法指导: 启发、引导、归纳、分类等
四、知识链接:(一)知识回顾,整体认识:
1、本章知识回顾
(1)空间点、线、面间的位置关系;
(2)直线、平面平行的判定及性质;
(3)直线、平面垂直的判定及性质。
2、本章知识结构框图:
(二)整合知识,发展思维
1、刻画平面的三个公理是立体几何公理体系的基石,是研究空间图形问题,进行逻辑推理的基础。
公理1——判定直线是否在平面内的依据;公理2——提供确定平面最基本的依据;
公理3——判定两个平面交线位置的依据;公理4——判定空间直线之间平行的依据。
2、空间问题解决的重要思想方法:化空间问题为平面问题;
3、空间平行、垂直之间的转化与联系:
【注】 :以上模块大约用时2-3分钟
五、学习过程:(本模块大约用时5-7分钟)
A1:下面四个命题:①分别在两个平面内的直线平行;②若两个平面平行,则其中一个平面内的任何一条直线必平行于另一个平面;③如果一个平面内的两条直线平行于另一个平面,则这两个平面平行;④如果一个平面内的任何一条直线都平行于另一个平面,则这两个平面平行.其中正确的命题是 : ( B )
A. ①② B. ②④ C. ①③ D. ②③
A2:设正方体的全面积为24,一个球内切于正方体,那么这个球的体积是 : ( D )
A. B. C. D.
A3:若三个平面两两相交,有三条交线,则下列命题中正确的是: ( D )
A. 三条交线为异面直线 B. 三条交线两两平行
C. 三条交线交与一点 D. 三条交线两两平行或交与一点
B4:菱形ABCD在平面内,,则PA与对角线BD的位置关系是 : ( D )
A.平行 B.相交但不垂直 C.垂直相交 D.异面垂直
六、当堂检测:(本模块大约用时25-27分钟)
B5:在正三棱柱ABC-中,若AB=,则与所成的角的大小为 : ( B )
A. B. C. D.
B6:设m、n是两条不同的直线,、是两个不同的平面,下列命题中正确的命题是:( B )
A. B.
C. D.
B7:如图所示,以等腰直角三角形斜边BC上的高AD为折痕,使 和折成互相垂直的两个平面,则
(1) BD与CD的关系为 :
(2) =
B8:已知A、B、C、D为空间四个点且A、B、C、D不共面,则直线AB与CD的位置关系是
异 面
C9:如图,已知ABCD是矩形,E是以CD为直径的半圆周上一点,且面CDE面ABCD,求证:CE平面ADE
证明:简证:面CDE面ABCD且ADDC,得ADCE又因为CEDE,得CE平面ADE
七、拓展迁移:
D10. 如图:在底面为平行四边形的四棱锥P-ABCD中,ABAC,PA平面ABCD,,点E是PD的中点,
求证:(1)ACPB (2)PB//平面AEC
证明:(2)提示连接BD交AC于点O则PA//EO即可证出
D11:如图,三棱柱ABC-中,D是BC上一点,且//平面,是的中点.
求证:平面//平面
证明:提示:连接交于点O,连接OD,则由已知可推出
//OD,则可推得OD是得中位线,则D是BC的中点,
则可证出,
则可证平面//平面
八、课堂小结:(本模块大约2-3分钟)
1.本节课对第二章的知识点进行了系统的复习,学生必须掌握。
2.通过习题的设置检测学生对本章的知识点的掌握情况
3.点火预热
九、课后反思:
.
课题:《第二章 点、线、面之间的位置关系》习题课一
高一数学学案40 设计人:唐桂荣 设计时间:5.5 授课时间: 组长签字:
一、学习目标
1.知识与能力:
(1)使学生掌握知识结构与联系,进一步巩固、深化所学知识;
(2)通过对知识的梳理,提高学生的归纳知识和综合运用知识的能力。
2.过程与方法:利用框图对本章知识进行系统的小结,直观、简明再现所学知识,化抽象学习为直观学习,易于识记;同时凸现数学知识的发展和联系。
3.态度与价值观:学生通过知识的整合、梳理,理会空间点、线面间的位置关系及其互相联系,进一步培养学生的空间想象能力和解决问题能力。
二、学习重点:知识点间的网络关系;
学习难点:在空间如何实现平行关系、垂直关系、垂直与平行关系之间的转化。
三、学法指导: 启发、引导、归纳、分类等
四、知识链接:(一)知识回顾,整体认识:
1、本章知识回顾
(1)空间点、线、面间的位置关系;
(2)直线、平面平行的判定及性质;
(3)直线、平面垂直的判定及性质。
2、本章知识结构框图:
(二)整合知识,发展思维
1、刻画平面的三个公理是立体几何公理体系的基石,是研究空间图形问题,进行逻辑推理的基础。
公理1——判定直线是否在平面内的依据;公理2——提供确定平面最基本的依据;
公理3——判定两个平面交线位置的依据;公理4——判定空间直线之间平行的依据。
2、空间问题解决的重要思想方法:化空间问题为平面问题;
3、空间平行、垂直之间的转化与联系:
【注】 :以上模块大约用时2-3分钟
高一( ) 班 . 第 ( )小组 . 姓名:
五、学习过程:(本模块大约用时5-7分钟)
A1:下面四个命题:①分别在两个平面内的直线平行;②若两个平面平行,则其中一个平面内的任何一条直线必平行于另一个平面;③如果一个平面内的两条直线平行于另一个平面,则这两个平面平行;④如果一个平面内的任何一条直线都平行于另一个平面,则这两个平面平行.其中正确的命题是 : ( )
A. ①② B. ②④ C. ①③ D. ②③
A2:设正方体的全面积为24,一个球内切于正方体,那么这个球的体积是 : ( )
A. B. C. D.
A3:若三个平面两两相交,有三条交线,则下列命题中正确的是: ( )
A. 三条交线为异面直线 B. 三条交线两两平行
C. 三条交线交与一点 D. 三条交线两两平行或交与一点
B4:菱形ABCD在平面内,,则PA与对角线BD的位置关系是 : ( )
A.平行 B.相交但不垂直 C.垂直相交 D.异面垂直
六、当堂检测:(本模块大约用时25-27分钟)
B5:在正三棱柱ABC-中,若AB=,则与所成的角的大小为 : ( )
A. B. C. D.
B6:设m、n是两条不同的直线,、是两个不同的平面,下列命题中正确的命题是:( )
A. B.
C. D.
B7:如图所示,以等腰直角三角形斜边BC上的高AD为折痕,使 和折成互相垂直的两个平面,则
(1) BD与CD的关系为
(2) =
B8:已知A、B、C、D为空间四个点且A、B、C、D不共面,
则直线AB与CD的位置关系是
C9:如图,已知ABCD是矩形,E是以CD为直径的半圆周上一点,且面CDE面ABCD,
求证:CE平面ADE
七、拓展迁移:
D10. 如图:在底面为平行四边形的四棱锥P-ABCD中, ABAC,PA平面ABCD,,点E是PD的中点,
求证:(1)ACPB (2)PB//平面AEC
D11:如图,三棱柱ABC-中,D是BC上一点,且//平面,是的中点.
求证:平面//平面
.
批改时间:第一次:2010年5 月 日 等级: 第二次:2010年5月 日
寄语: 只要再多一点努力,你就会多一点成功.
平面(公理1、公理2、公理3、公理4)
空间直线、平面的位置关系
直线与直线的位置关系
直线与平面的位置关系
平面与平面的位置关系
平面与平面平行
直线与直线平行
直线与平面平行
直线与平面垂直
平面与平面垂直
直线与直线垂直
平面(公理1、公理2、公理3、公理4)
空间直线、平面的位置关系
直线与直线的位置关系
直线与平面的位置关系
平面与平面的位置关系
平面与平面平行
直线与直线平行
直线与平面平行
直线与平面垂直
平面与平面垂直
直线与直线垂直
