两角差的余弦公式
图片预览







文档简介
课件20张PPT。 太子灵踪塔,即宝相寺塔。俗称“黄金塔”。座落在山东 省汶上县西北隅,始建于唐,是屈指可数的中国佛教建筑之一。 思考:现从围墙外测量塔的高度,可以怎样测量?
BD= AB tan60°= 如图所示,可在地平面取一点
A,测得A、C两点间距离约为27米,
从A观测塔的视角(∠CAD)为45°
∠CAB=15°。试求塔的高度。
想一想?问题: 已知 , 那么.
COS15°=COS(60°-45°)=?大家可以猜想,
是不是等于 COS60°-COS45°呢?
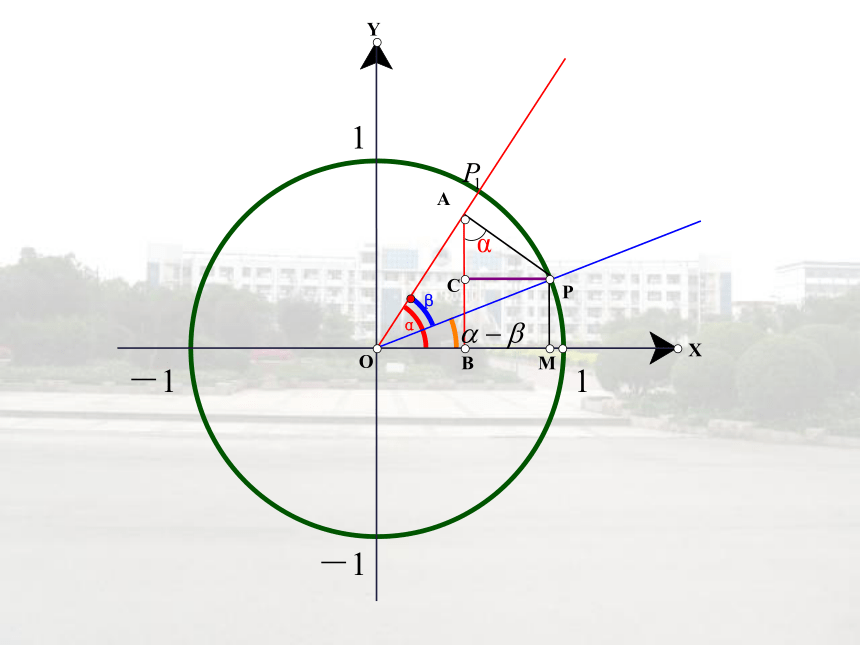
易知 : 探究:如何用任意角α,β的正弦、余弦值表示 ?两角差的余弦公式βαCBAMPOXYα1-11-1(1)、结合图形,明确 可以表示成哪两个向量的夹角,它们怎么表示?
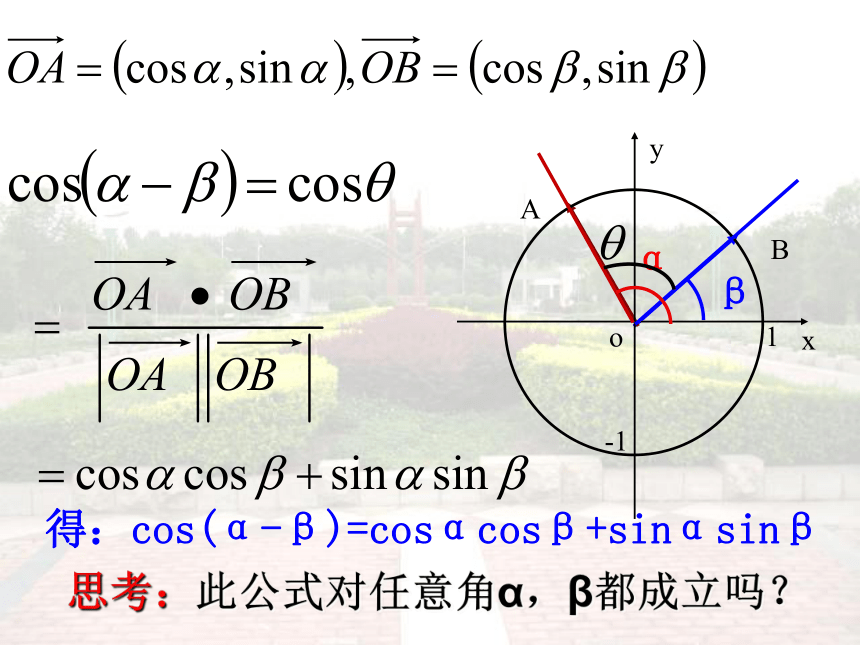
(2)、怎样利用向量数量积的概念和计算公式得到探索结果?得:cos(α-β)=cosαcosβ+sinαsinβ思考:此公式对任意角α,β都成立吗?若 则 若 则 且 ABβθα于是,对于任意角α、β都有 ①任意角 ②同名积 ③符号反两角差的余弦公式 例1:利用余弦公式求 的值分析:此题关键是把15°的角分解成两个特殊角的差。解法一:
学以致用!公式的正用!解法二: 试求:cos75°,sin75°的值 BD= AB tan60°= 所以 塔高为: 米 分析:根据公式的条件,需求出cosα与sinβ的值 例2 已知β是第三象限角,求 的值。解:由得又由β是第三象限角, 得所以为什么取负的?为什么取负的?强调:
角的范围!变式训练:将题目中的条件 去掉,
对解题的过程和结果会有什么影响?如何求解?答案: 当 是第一象限角时:
当 是第二象限角时:公式的逆用!
(1)cos115°cos25°+sin115°sin25° (2) (4)(3)cos80°cos35°+cos10°cos55°公式的变形!思考题:已知 都是锐角, 求的值。作业: (1) 阅读课本,体验公式的得出,证明过程;
分析公式结构,通过习题加强公式的灵活应用.
(2) 完成课本第127页2,3,4题. 同学们再见
BD= AB tan60°= 如图所示,可在地平面取一点
A,测得A、C两点间距离约为27米,
从A观测塔的视角(∠CAD)为45°
∠CAB=15°。试求塔的高度。
想一想?问题: 已知 , 那么.
COS15°=COS(60°-45°)=?大家可以猜想,
是不是等于 COS60°-COS45°呢?
易知 : 探究:如何用任意角α,β的正弦、余弦值表示 ?两角差的余弦公式βαCBAMPOXYα1-11-1(1)、结合图形,明确 可以表示成哪两个向量的夹角,它们怎么表示?
(2)、怎样利用向量数量积的概念和计算公式得到探索结果?得:cos(α-β)=cosαcosβ+sinαsinβ思考:此公式对任意角α,β都成立吗?若 则 若 则 且 ABβθα于是,对于任意角α、β都有 ①任意角 ②同名积 ③符号反两角差的余弦公式 例1:利用余弦公式求 的值分析:此题关键是把15°的角分解成两个特殊角的差。解法一:
学以致用!公式的正用!解法二: 试求:cos75°,sin75°的值 BD= AB tan60°= 所以 塔高为: 米 分析:根据公式的条件,需求出cosα与sinβ的值 例2 已知β是第三象限角,求 的值。解:由得又由β是第三象限角, 得所以为什么取负的?为什么取负的?强调:
角的范围!变式训练:将题目中的条件 去掉,
对解题的过程和结果会有什么影响?如何求解?答案: 当 是第一象限角时:
当 是第二象限角时:公式的逆用!
(1)cos115°cos25°+sin115°sin25° (2) (4)(3)cos80°cos35°+cos10°cos55°公式的变形!思考题:已知 都是锐角, 求的值。作业: (1) 阅读课本,体验公式的得出,证明过程;
分析公式结构,通过习题加强公式的灵活应用.
(2) 完成课本第127页2,3,4题. 同学们再见
