《第二章 点、线、面之间的位置关系》习题二
文档属性
| 名称 | 《第二章 点、线、面之间的位置关系》习题二 |
|
|
| 格式 | zip | ||
| 文件大小 | 70.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-06 00:00:00 | ||
图片预览

文档简介
课题:《第二章 点、线、面之间的位置关系》习题二
高一数学教案41 设计人:唐桂荣 设计时间:5.9 授课时间: 组长签字:
一、教学目标:
1.知识与能力:
(1)使学生掌握知识结构与联系,进一步巩固、深化所学知识;
(2)通过对知识的梳理,提高学生的归纳知识和综合运用知识的能力。
2.过程与方法:利用框图对本章知识进行系统的小结,直观、简明再现所学知识,化抽象学习为直观学习,易于识记;同时凸现数学知识的发展和联系。
3.态度与价值观:学生通过知识的整合、梳理,理会空间点、线面间的位置关系及其互相联系,进一步培养学生的空间想象能力和解决问题能力。
二、教学重点:知识点间的网络关系;
教学难点:在空间如何实现平行关系、垂直关系、垂直与平行关系之间的转化。
三、学法指导: 启发、引导、归纳、分类等
四、知识链接:本章知识回顾
(1)空间点、线、面间的位置关系;
(2)直线、平面平行的判定及性质;
(3)直线、平面垂直的判定及性质。
【注】 :以上模块大约用时2-3分钟
五、学习过程:(本模块大约用时4-5分钟)
A1.若三个平面两两相交,且三条交线平行,则这三个平面把空间分成( C)
A.5部分 B 。6部分 C。7部分 D。8部分
A2.下列四个命题:①若直线a与b异面,b与c异面,则a与c异面。②若直线a与b相交,b与c相交,则a与c相交。③若直线a//b, b//c, 则a//b//c ④若直线a//b,则a,b与直线c所成的角相等。其中真命题的个数是 ( C )
A。4 B。3 C。2 D。1
A3.如图,在中,,,
AB=AC,D是BC的中点,则图中直角三角形的个数是 ( B )
A.5 B.8 C.10 D.6
B4:如图:三棱锥P-ABC的顶点P在底面ABC内射影为O
(O在内部,即过P作,交与O), 且
P到AB.BC.CD距离相等,则O是的 ( C )
A.外心。 B. 垂心 C.内心 D.重心
六、当堂检测:(本模块大约用时28-30分钟)
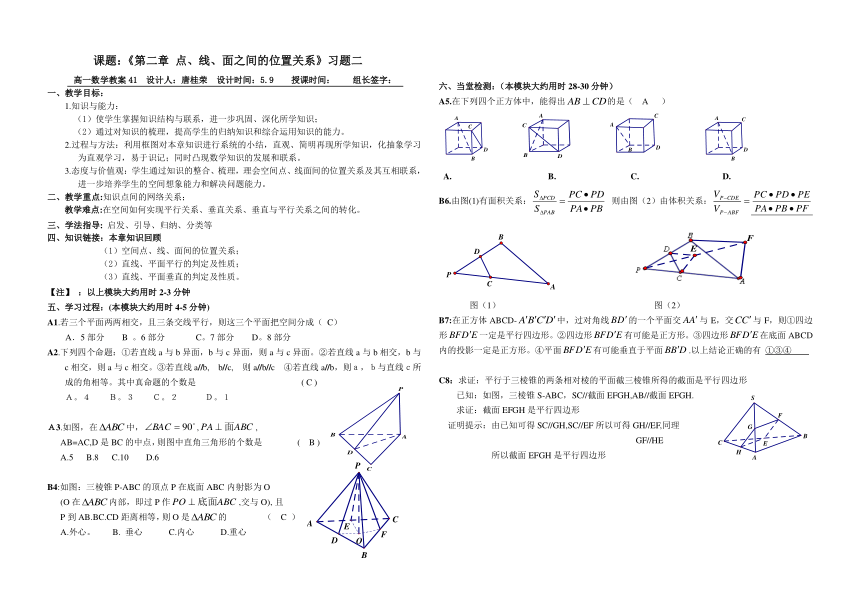
A5.在下列四个正方体中,能得出的是( A )
A. B. C. D.
B6.由图(1)有面积关系: 则由图(2)由体积关系:
图(1) 图(2)
B7:在正方体ABCD-中,过对角线的一个平面交与E,交与F,则①四边形一定是平行四边形。②四边形有可能是正方形。③四边形在底面ABCD内的投影一定是正方形。④平面有可能垂直于平面.以上结论正确的有 ①③④
C8:求证:平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形
已知:如图,三棱锥S-ABC,SC//截面EFGH,AB//截面EFGH.
求证:截面EFGH是平行四边形
证明提示:由已知可得SC//GH,SC//EF所以可得GH//EF,同理
GF//HE
所以截面EFGH是平行四边形
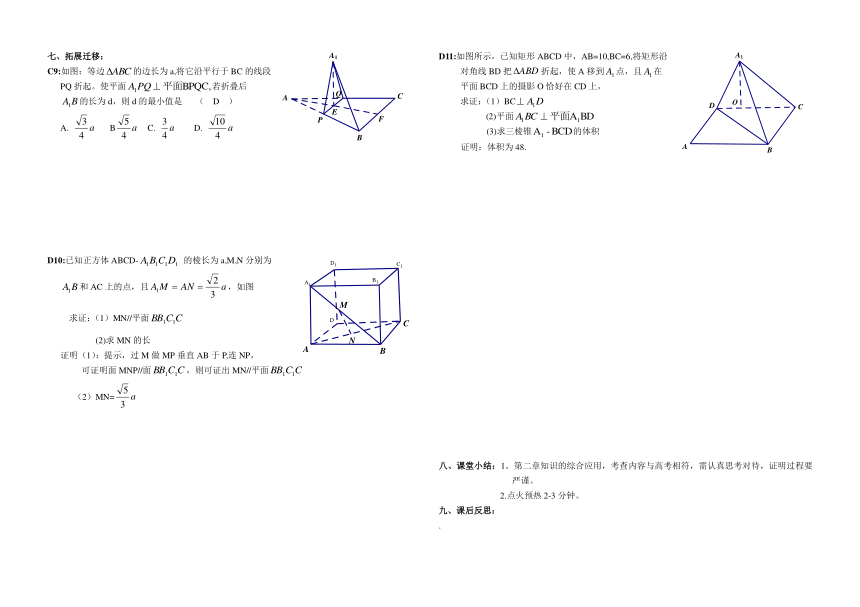
七、拓展迁移:
C9:如图:等边的边长为a,将它沿平行于BC的线段
PQ折起。使平面若折叠后
的长为d,则d的最小值是 ( D )
A. B C. D.
D10:已知正方体ABCD- 的棱长为a,M,N分别为
和AC上的点,且,如图
求证:(1)MN//平面
(2)求MN的长
证明(1):提示,过M做MP垂直AB于P,连NP,
可证明面MNP//面,则可证出MN//平面
(2)MN=
D11:如图所示,已知矩形ABCD中,AB=10,BC=6,将矩形沿
对角线BD把折起,使A移到点,且在
平面BCD上的摄影O恰好在CD上,
求证:(1)BC
(2)平面
(3)求三棱锥的体积
证明:体积为48.
八、课堂小结:1。第二章知识的综合应用,考查内容与高考相符,需认真思考对待,证明过程要严谨。
2.点火预热2-3分钟。
九、课后反思:
.
课题:《第二章 点、线、面之间的位置关系》习题二
高一数学学案41 设计人:唐桂荣 设计时间:5.9 授课时间: 组长签字:
一、学习目标:
1.知识与能力:
(1)使学生掌握知识结构与联系,进一步巩固、深化所学知识;
(2)通过对知识的梳理,提高学生的归纳知识和综合运用知识的能力。
2.过程与方法:利用框图对本章知识进行系统的小结,直观、简明再现所学知识,化抽象学习为直观学习,易于识记;同时凸现数学知识的发展和联系。
3.态度与价值观:学生通过知识的整合、梳理,理会空间点、线面间的位置关系及其互相联系,进一步培养学生的空间想象能力和解决问题能力。
二、学习重点:知识点间的网络关系;
学习难点:在空间如何实现平行关系、垂直关系、垂直与平行关系之间的转化。
三、学法指导: 启发、引导、归纳、分类等
四、知识链接:本章知识回顾
(1)空间点、线、面间的位置关系;
(2)直线、平面平行的判定及性质;
(3)直线、平面垂直的判定及性质。
【注】 :以上模块大约用时2-3分钟
五、学习过程:(本模块大约用时4-5分钟)
A1.若三个平面两两相交,且三条交线平行,则这三个平面把空间分成( )
A.5部分 B 。6部分 C。7部分 D。8部分
A2.下列四个命题:①若直线a与b异面,b与c异面,则a与c异面。②若直线a与b相交,b与c相交,则a与c相交。③若直线a//b, b//c, 则a//b//c ④若直线a//b,则a,b与直线c所成的角相等。其中真命题的个数是 ( )
A。4 B。3 C。2 D。1
A3.如图,在中,,,
AB=AC,D是BC的中点,则图中直角三角形的个数是 ( )
A.5 B.8 C.10 D.6
B4:如图:三棱锥P-ABC的顶点P在底面ABC内射影为O
(O在内部,即过P作,交与O), 且
P到AB、BC、CD距离相等,则O是的 ( )
A.外心。 B. 垂心 C.内心 D.重心
高一( ) 班 . 第 ( )小组 . 姓名:
六、当堂检测:(本模块大约用时28-30分钟)
A5.在下列四个正方体中,能得出的是( )
.
A. B. C. D.
B6.由图(1)有面积关系: 则由图(2)由体积关系:
图(1) 图(2)
B7:在正方体ABCD-中,过对角线的一个平面交与E,交与F,则①四边形一定是平行四边形。②四边形有可能是正方形。③四边形在底面ABCD内的投影一定是正方形。④平面有可能垂直于平面.以上结论正确的有
C8:求证:平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形
已知:如图,三棱锥S-ABC,SC//截面EFGH,AB//截面EFGH.
求证:截面EFGH是平行四边形
七、拓展迁移:
C9:如图:等边的边长为a,将它沿平行于BC的线段
PQ折起。使平面若折叠后
的长为d,则d的最小值是 ( )
A. B C. D.
D9:已知正方体ABCD- 的棱长为a,M,N分别为
和AC上的点,且,如图
求证:(1)MN//平面
(2)求MN的长
D10:如图所示,已知矩形ABCD中,AB=10,BC=6,将矩形沿
对角线BD把折起,使A移到点,且在
平面BCD上的摄影O恰好在CD上,
求证:(1)BC
(2)平面
(3)求三棱锥的体积
.
批改时间:第一次:2010年5 月 日 等级: 第二次:2010年5月 日
寄语: 只要再多一点努力,你就会多一点成功.
高一数学教案41 设计人:唐桂荣 设计时间:5.9 授课时间: 组长签字:
一、教学目标:
1.知识与能力:
(1)使学生掌握知识结构与联系,进一步巩固、深化所学知识;
(2)通过对知识的梳理,提高学生的归纳知识和综合运用知识的能力。
2.过程与方法:利用框图对本章知识进行系统的小结,直观、简明再现所学知识,化抽象学习为直观学习,易于识记;同时凸现数学知识的发展和联系。
3.态度与价值观:学生通过知识的整合、梳理,理会空间点、线面间的位置关系及其互相联系,进一步培养学生的空间想象能力和解决问题能力。
二、教学重点:知识点间的网络关系;
教学难点:在空间如何实现平行关系、垂直关系、垂直与平行关系之间的转化。
三、学法指导: 启发、引导、归纳、分类等
四、知识链接:本章知识回顾
(1)空间点、线、面间的位置关系;
(2)直线、平面平行的判定及性质;
(3)直线、平面垂直的判定及性质。
【注】 :以上模块大约用时2-3分钟
五、学习过程:(本模块大约用时4-5分钟)
A1.若三个平面两两相交,且三条交线平行,则这三个平面把空间分成( C)
A.5部分 B 。6部分 C。7部分 D。8部分
A2.下列四个命题:①若直线a与b异面,b与c异面,则a与c异面。②若直线a与b相交,b与c相交,则a与c相交。③若直线a//b, b//c, 则a//b//c ④若直线a//b,则a,b与直线c所成的角相等。其中真命题的个数是 ( C )
A。4 B。3 C。2 D。1
A3.如图,在中,,,
AB=AC,D是BC的中点,则图中直角三角形的个数是 ( B )
A.5 B.8 C.10 D.6
B4:如图:三棱锥P-ABC的顶点P在底面ABC内射影为O
(O在内部,即过P作,交与O), 且
P到AB.BC.CD距离相等,则O是的 ( C )
A.外心。 B. 垂心 C.内心 D.重心
六、当堂检测:(本模块大约用时28-30分钟)
A5.在下列四个正方体中,能得出的是( A )
A. B. C. D.
B6.由图(1)有面积关系: 则由图(2)由体积关系:
图(1) 图(2)
B7:在正方体ABCD-中,过对角线的一个平面交与E,交与F,则①四边形一定是平行四边形。②四边形有可能是正方形。③四边形在底面ABCD内的投影一定是正方形。④平面有可能垂直于平面.以上结论正确的有 ①③④
C8:求证:平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形
已知:如图,三棱锥S-ABC,SC//截面EFGH,AB//截面EFGH.
求证:截面EFGH是平行四边形
证明提示:由已知可得SC//GH,SC//EF所以可得GH//EF,同理
GF//HE
所以截面EFGH是平行四边形
七、拓展迁移:
C9:如图:等边的边长为a,将它沿平行于BC的线段
PQ折起。使平面若折叠后
的长为d,则d的最小值是 ( D )
A. B C. D.
D10:已知正方体ABCD- 的棱长为a,M,N分别为
和AC上的点,且,如图
求证:(1)MN//平面
(2)求MN的长
证明(1):提示,过M做MP垂直AB于P,连NP,
可证明面MNP//面,则可证出MN//平面
(2)MN=
D11:如图所示,已知矩形ABCD中,AB=10,BC=6,将矩形沿
对角线BD把折起,使A移到点,且在
平面BCD上的摄影O恰好在CD上,
求证:(1)BC
(2)平面
(3)求三棱锥的体积
证明:体积为48.
八、课堂小结:1。第二章知识的综合应用,考查内容与高考相符,需认真思考对待,证明过程要严谨。
2.点火预热2-3分钟。
九、课后反思:
.
课题:《第二章 点、线、面之间的位置关系》习题二
高一数学学案41 设计人:唐桂荣 设计时间:5.9 授课时间: 组长签字:
一、学习目标:
1.知识与能力:
(1)使学生掌握知识结构与联系,进一步巩固、深化所学知识;
(2)通过对知识的梳理,提高学生的归纳知识和综合运用知识的能力。
2.过程与方法:利用框图对本章知识进行系统的小结,直观、简明再现所学知识,化抽象学习为直观学习,易于识记;同时凸现数学知识的发展和联系。
3.态度与价值观:学生通过知识的整合、梳理,理会空间点、线面间的位置关系及其互相联系,进一步培养学生的空间想象能力和解决问题能力。
二、学习重点:知识点间的网络关系;
学习难点:在空间如何实现平行关系、垂直关系、垂直与平行关系之间的转化。
三、学法指导: 启发、引导、归纳、分类等
四、知识链接:本章知识回顾
(1)空间点、线、面间的位置关系;
(2)直线、平面平行的判定及性质;
(3)直线、平面垂直的判定及性质。
【注】 :以上模块大约用时2-3分钟
五、学习过程:(本模块大约用时4-5分钟)
A1.若三个平面两两相交,且三条交线平行,则这三个平面把空间分成( )
A.5部分 B 。6部分 C。7部分 D。8部分
A2.下列四个命题:①若直线a与b异面,b与c异面,则a与c异面。②若直线a与b相交,b与c相交,则a与c相交。③若直线a//b, b//c, 则a//b//c ④若直线a//b,则a,b与直线c所成的角相等。其中真命题的个数是 ( )
A。4 B。3 C。2 D。1
A3.如图,在中,,,
AB=AC,D是BC的中点,则图中直角三角形的个数是 ( )
A.5 B.8 C.10 D.6
B4:如图:三棱锥P-ABC的顶点P在底面ABC内射影为O
(O在内部,即过P作,交与O), 且
P到AB、BC、CD距离相等,则O是的 ( )
A.外心。 B. 垂心 C.内心 D.重心
高一( ) 班 . 第 ( )小组 . 姓名:
六、当堂检测:(本模块大约用时28-30分钟)
A5.在下列四个正方体中,能得出的是( )
.
A. B. C. D.
B6.由图(1)有面积关系: 则由图(2)由体积关系:
图(1) 图(2)
B7:在正方体ABCD-中,过对角线的一个平面交与E,交与F,则①四边形一定是平行四边形。②四边形有可能是正方形。③四边形在底面ABCD内的投影一定是正方形。④平面有可能垂直于平面.以上结论正确的有
C8:求证:平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形
已知:如图,三棱锥S-ABC,SC//截面EFGH,AB//截面EFGH.
求证:截面EFGH是平行四边形
七、拓展迁移:
C9:如图:等边的边长为a,将它沿平行于BC的线段
PQ折起。使平面若折叠后
的长为d,则d的最小值是 ( )
A. B C. D.
D9:已知正方体ABCD- 的棱长为a,M,N分别为
和AC上的点,且,如图
求证:(1)MN//平面
(2)求MN的长
D10:如图所示,已知矩形ABCD中,AB=10,BC=6,将矩形沿
对角线BD把折起,使A移到点,且在
平面BCD上的摄影O恰好在CD上,
求证:(1)BC
(2)平面
(3)求三棱锥的体积
.
批改时间:第一次:2010年5 月 日 等级: 第二次:2010年5月 日
寄语: 只要再多一点努力,你就会多一点成功.
