多边形内角和与外角和课件
文档属性
| 名称 | 多边形内角和与外角和课件 |  | |
| 格式 | rar | ||
| 文件大小 | 385.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-05 22:31:00 | ||
图片预览




文档简介
课件18张PPT。多边形的内角和与外角和茶棚中学 陈兴旺生活中的多边形形象
1、了解多边形,多边形的内角,外角,对角线,外角和,正多边形等概念。
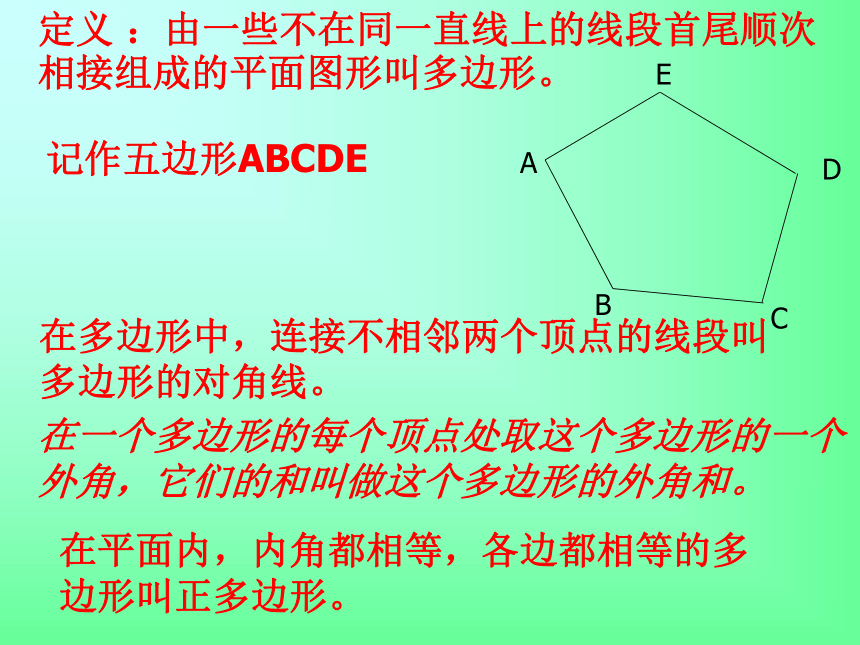
2、能用不同的方法探索多边形的内角和与外角和公式,并会运用它们进行有关计算。学习目标定义 :由一些不在同一直线上的线段首尾顺次相接组成的平面图形叫多边形。 ABCDE
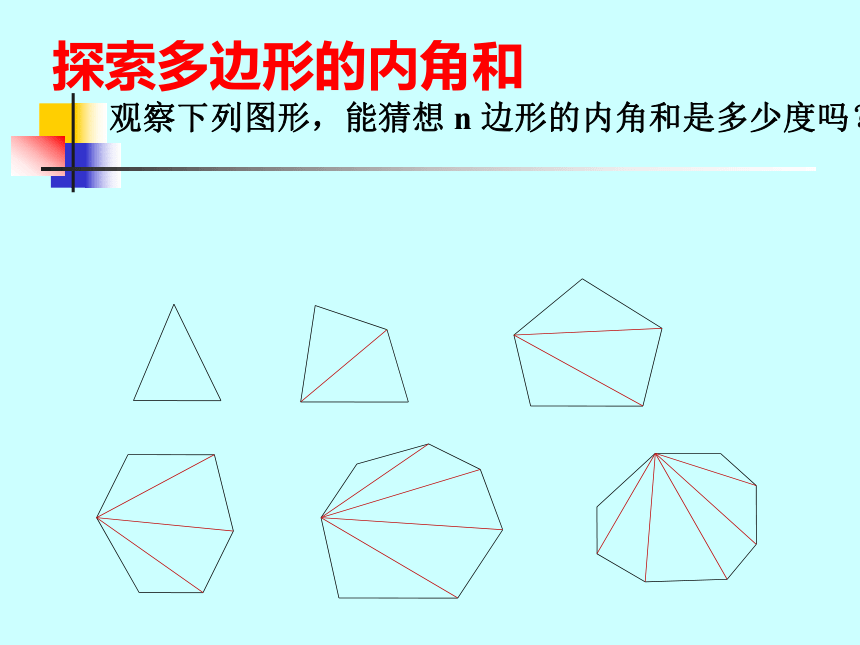
记作五边形ABCDE在多边形中,连接不相邻两个顶点的线段叫多边形的对角线。在平面内,内角都相等,各边都相等的多边形叫正多边形。在一个多边形的每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。观察下列图形,能猜想 n 边形的内角和是多少度吗?探索多边形的内角和请你完成下面的这个表格:(n-2)×180 °900 °720 °540 °360 °
n-2
5
4
3
2n边形的内角和为 。(n-2)×180 °如图:在n边形内任取一点p,连结点p与多边形的每一个顶点,可得几个三角形?(图中取n为6 的情形)你能根据图中这样划分多边形的方法来说明n边形的内角和等于(n-2)×180o?
ABCDEFP多边形的外角和 指出右边多边形的内角与外角。 多边形的外角与它相邻的内角的关系 。 请你动手来实践一下,看看谁能最先找出来四边形的外角和?互补360 °360 °360 °360 °(n-2)×180°720 °540 °360 °n×180°6×180° =1080 °5×180°=900 °4×180° =720 °请你完成下面的这个表格: 推论:任意多边形的外角 和
等于360o 。 我是这样想的: ∵ n边形的每一个外角与它相邻的内角的和是_____
∴ n边形的内角和加外角和等于 ________
∵ n 边形的内角和等于 ___________A1A2A3AnA4证明:180o ,(n-2) ? 180o ,∴ n 边形的外角和等于n ? 180o – (n-2) ? 180o =360o。n ? 180o,例题1已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。解:设多边形的边数为n ,
∵它的内角和等于(n-2) ? 180o ,外角
和等于360o ,
∴ (n-2)×180o=2 × 360o
解得 n=6
∴这个多边形的边数6
1、n边形的内角和是(n-2)·180o,揭示了多
边形的内角和与边数的关系:当边数增
加1时,内角和增加180o。2、任意多边形的外角和都是360o,与边数
无关。多边形的内角和小结能力训练:1、正八边形的内角和是( ),每个内角的度数是 ( ) 。2、一多边形的每个内角都等于120°,则其每一个外角是( ) ,它是( ) 边形。3、一多边形的内角和1260 ° ,则其边数( ) 。4、一个多边形的每个外角都是30 ° ,则此多边形的内角和是 ( ) 。5、五边形的内角和与外角和的比值是( ) 。1080 °135 °60 °六九1800 °3:2开放创新题把一个长方形的桌子截去一个角,得到的多边形的内角和是几度?聪明题
已知: 如图 ∠A,∠B,∠C,
∠D,∠E,∠F,∠G,∠H八个
角的和的度数是多少度?一、填空题
十二边形的内角和是( )。
正六边形的一个内角等于( )。
一个多边形当边数增加1时,它的内角和增加( )。
一个多边形的内角和等于它的外角和,这个多边形是 ( )边形。
一个多边形的内角和是720o,则此多边形共有( )个内角。1800o120o180o四六
2、能用不同的方法探索多边形的内角和与外角和公式,并会运用它们进行有关计算。学习目标定义 :由一些不在同一直线上的线段首尾顺次相接组成的平面图形叫多边形。 ABCDE
记作五边形ABCDE在多边形中,连接不相邻两个顶点的线段叫多边形的对角线。在平面内,内角都相等,各边都相等的多边形叫正多边形。在一个多边形的每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。观察下列图形,能猜想 n 边形的内角和是多少度吗?探索多边形的内角和请你完成下面的这个表格:(n-2)×180 °900 °720 °540 °360 °
n-2
5
4
3
2n边形的内角和为 。(n-2)×180 °如图:在n边形内任取一点p,连结点p与多边形的每一个顶点,可得几个三角形?(图中取n为6 的情形)你能根据图中这样划分多边形的方法来说明n边形的内角和等于(n-2)×180o?
ABCDEFP多边形的外角和 指出右边多边形的内角与外角。 多边形的外角与它相邻的内角的关系 。 请你动手来实践一下,看看谁能最先找出来四边形的外角和?互补360 °360 °360 °360 °(n-2)×180°720 °540 °360 °n×180°6×180° =1080 °5×180°=900 °4×180° =720 °请你完成下面的这个表格: 推论:任意多边形的外角 和
等于360o 。 我是这样想的: ∵ n边形的每一个外角与它相邻的内角的和是_____
∴ n边形的内角和加外角和等于 ________
∵ n 边形的内角和等于 ___________A1A2A3AnA4证明:180o ,(n-2) ? 180o ,∴ n 边形的外角和等于n ? 180o – (n-2) ? 180o =360o。n ? 180o,例题1已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。解:设多边形的边数为n ,
∵它的内角和等于(n-2) ? 180o ,外角
和等于360o ,
∴ (n-2)×180o=2 × 360o
解得 n=6
∴这个多边形的边数6
1、n边形的内角和是(n-2)·180o,揭示了多
边形的内角和与边数的关系:当边数增
加1时,内角和增加180o。2、任意多边形的外角和都是360o,与边数
无关。多边形的内角和小结能力训练:1、正八边形的内角和是( ),每个内角的度数是 ( ) 。2、一多边形的每个内角都等于120°,则其每一个外角是( ) ,它是( ) 边形。3、一多边形的内角和1260 ° ,则其边数( ) 。4、一个多边形的每个外角都是30 ° ,则此多边形的内角和是 ( ) 。5、五边形的内角和与外角和的比值是( ) 。1080 °135 °60 °六九1800 °3:2开放创新题把一个长方形的桌子截去一个角,得到的多边形的内角和是几度?聪明题
已知: 如图 ∠A,∠B,∠C,
∠D,∠E,∠F,∠G,∠H八个
角的和的度数是多少度?一、填空题
十二边形的内角和是( )。
正六边形的一个内角等于( )。
一个多边形当边数增加1时,它的内角和增加( )。
一个多边形的内角和等于它的外角和,这个多边形是 ( )边形。
一个多边形的内角和是720o,则此多边形共有( )个内角。1800o120o180o四六
