13.2命题与证明(第三课时)课件
图片预览



文档简介
课件15张PPT。13.2 命题与证明
第三课时 沪科版八年级数学上第13章《三角形中的边角关系、命题与证明》本节课学习目标1.如何证明三角形内角和等于180°?
理解将三角形内角和转化为“平角” 化归思想。
2.什么是辅助线?
添加辅助线应注意的事项?
3.掌握三角形内角和定理的推论1、
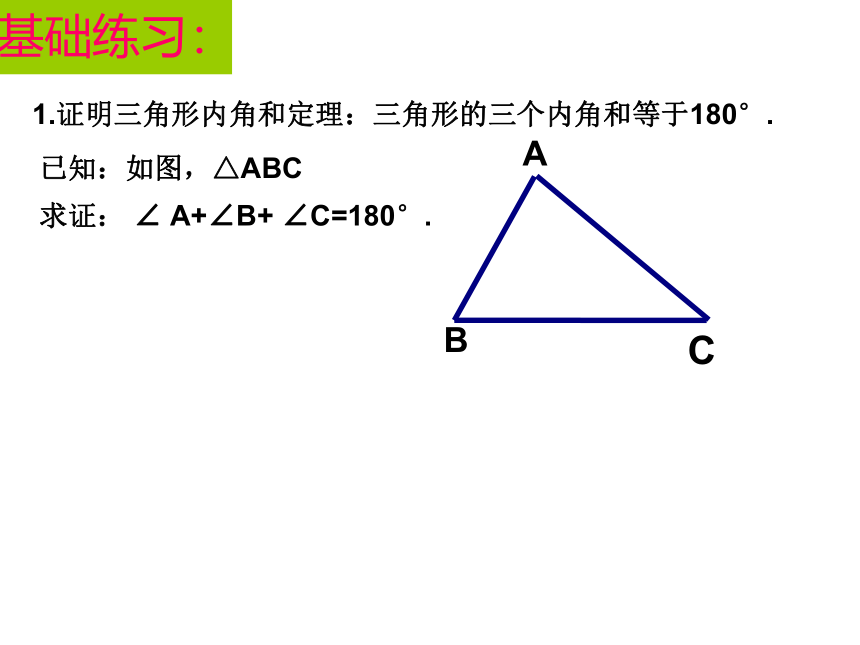
推论2.基础练习:1.证明三角形内角和定理:三角形的三个内角和等于180°.已知:如图,△ABC求证: ∠ A+∠B+ ∠C=180°.∵ ∠2=∠B
∴ CE∥BA
∴∠1=∠A
又∵∠1+∠2+∠ACB=180°
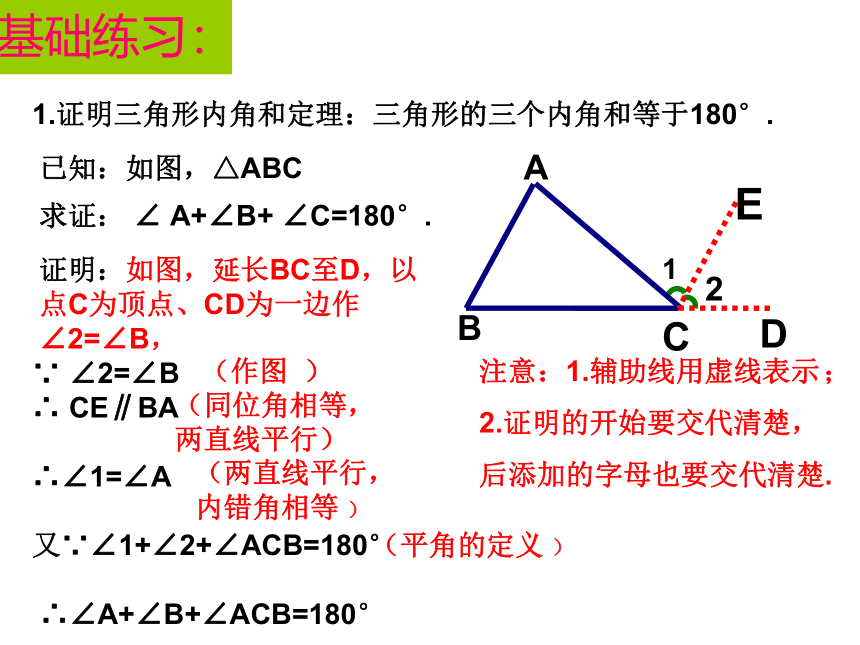
∴∠A+∠B+∠ACB=180°基础练习:1.证明三角形内角和定理:三角形的三个内角和等于180°.已知:如图,△ABC求证: ∠ A+∠B+ ∠C=180°.注意:1.辅助线用虚线表示 ;
2.证明的开始要交代清楚,
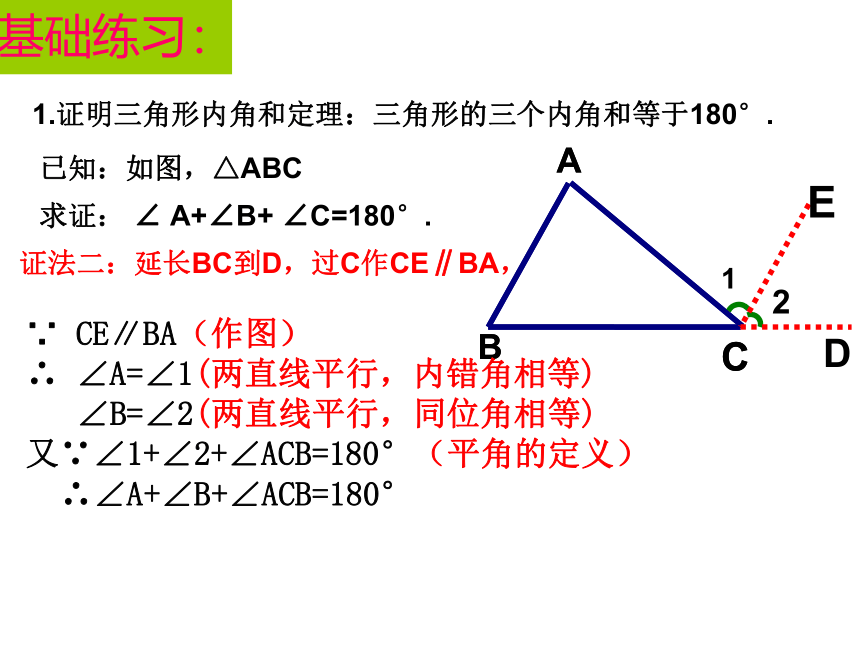
后添加的字母也要交代清楚.证明:如图,延长BC至D,以点C为顶点、CD为一边作∠2=∠B,(作图 )(同位角相等, 两直线平行)(两直线平行,内错角相等 )(平角的定义 )基础练习:1.证明三角形内角和定理:三角形的三个内角和等于180°.已知:如图,△ABC求证: ∠ A+∠B+ ∠C=180°.证法二:延长BC到D,过C作CE∥BA,∵ CE∥BA(作图)
∴ ∠A=∠1(两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°(平角的定义)
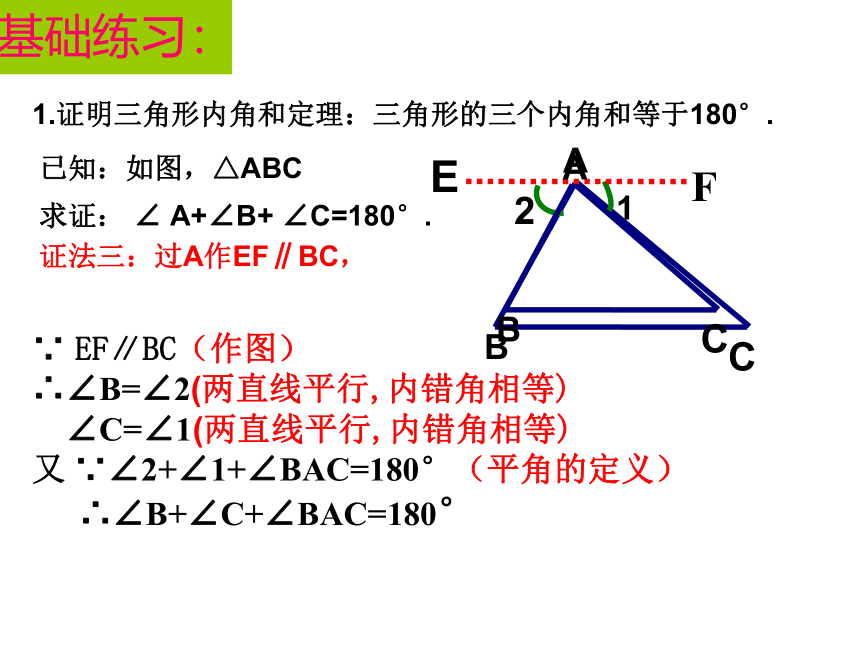
∴∠A+∠B+∠ACB=180°基础练习:1.证明三角形内角和定理:三角形的三个内角和等于180°.已知:如图,△ABC求证: ∠ A+∠B+ ∠C=180°.证法三:过A作EF∥BC,∵ EF∥BC(作图)
∴∠B=∠2(两直线平行,内错角相等)
∠C=∠1(两直线平行,内错角相等)
又 ∵∠2+∠1+∠BAC=180°(平角的定义)
∴∠B+∠C+∠BAC=180°你还有其他方法来证明三角形内角和定理吗?添加辅助线思路:1、构造平角 2、构造同旁内角提高训练下面的正六边形,你能根据自己的知识求出六边形的内角和吗?4个三角形:180°×4=720°提高训练六角螺母的面是六边形,它的内角都相等,
则这个六边形的每个内角是 。
120°分析研究表格,你能从中发现什么规律?56234360°540°720°提高训练 180°× (n-2)n边形nn-2当堂检测:1.证明课本81页的推论1、推论2.
2.等边三角形的一个内角是多少度?
并证明你的结论.
本节课学习了什么内容?三角形内角和定理三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.三角形内角和定理的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. 作业布置:
书面作业:
1、p84习题:6、7。
课外作业:
1、p81练习:1、2。
2、同步完成基训
3、预习下一节新课。再见
理解将三角形内角和转化为“平角” 化归思想。
2.什么是辅助线?
添加辅助线应注意的事项?
3.掌握三角形内角和定理的推论1、
推论2.基础练习:1.证明三角形内角和定理:三角形的三个内角和等于180°.已知:如图,△ABC求证: ∠ A+∠B+ ∠C=180°.∵ ∠2=∠B
∴ CE∥BA
∴∠1=∠A
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°基础练习:1.证明三角形内角和定理:三角形的三个内角和等于180°.已知:如图,△ABC求证: ∠ A+∠B+ ∠C=180°.注意:1.辅助线用虚线表示 ;
2.证明的开始要交代清楚,
后添加的字母也要交代清楚.证明:如图,延长BC至D,以点C为顶点、CD为一边作∠2=∠B,(作图 )(同位角相等, 两直线平行)(两直线平行,内错角相等 )(平角的定义 )基础练习:1.证明三角形内角和定理:三角形的三个内角和等于180°.已知:如图,△ABC求证: ∠ A+∠B+ ∠C=180°.证法二:延长BC到D,过C作CE∥BA,∵ CE∥BA(作图)
∴ ∠A=∠1(两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°(平角的定义)
∴∠A+∠B+∠ACB=180°基础练习:1.证明三角形内角和定理:三角形的三个内角和等于180°.已知:如图,△ABC求证: ∠ A+∠B+ ∠C=180°.证法三:过A作EF∥BC,∵ EF∥BC(作图)
∴∠B=∠2(两直线平行,内错角相等)
∠C=∠1(两直线平行,内错角相等)
又 ∵∠2+∠1+∠BAC=180°(平角的定义)
∴∠B+∠C+∠BAC=180°你还有其他方法来证明三角形内角和定理吗?添加辅助线思路:1、构造平角 2、构造同旁内角提高训练下面的正六边形,你能根据自己的知识求出六边形的内角和吗?4个三角形:180°×4=720°提高训练六角螺母的面是六边形,它的内角都相等,
则这个六边形的每个内角是 。
120°分析研究表格,你能从中发现什么规律?56234360°540°720°提高训练 180°× (n-2)n边形nn-2当堂检测:1.证明课本81页的推论1、推论2.
2.等边三角形的一个内角是多少度?
并证明你的结论.
本节课学习了什么内容?三角形内角和定理三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.三角形内角和定理的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. 作业布置:
书面作业:
1、p84习题:6、7。
课外作业:
1、p81练习:1、2。
2、同步完成基训
3、预习下一节新课。再见
