15.2线段的垂直平分线课件
图片预览







文档简介
课件22张PPT。第一环节 创设情境 导入新课 如图,A、B表示两个仓库,要在A、B一侧的河岸边建造
一个码头,使它到两个仓库的距离相等,码头应建在什么位置?第一章 三角形的证明 1.3 线段的垂直平分线 –-(1)第二环节 性质探索与证明命题:
线段垂直平分线上的点到这条线段两个端点的距离相等 如果 ,
那么 . 分析命题的条件和结论一个点在线段的垂直平分线上这个点到这条线段两个端点的距离相等第二环节 性质探索与证明2、根据条件和结论写出已知和求证 已知:
求证: PA=PB直线 l ⊥AB,垂足是C, AC=BC,
P是l上的任意一点. ∵ l⊥AB (已知)
∴∠PCA=∠PCB=90°(垂直定义)
∵AC=BC(已知)
PC=PC(公共边)
∴△PCA≌△PCB(SAS)
∴PA=PB(全等三角形的对应边相等)_P.证明:第二环节 性质探索与证明3、 线段垂直平分线的性质定理:
线段垂直平分线上的点到这条线段两个端点的距离相等. 如图
∵l是AB的垂直平分线,点P是直线l上一点
用几何推理符号语言怎么表示性质定理?
∴PA=PB或写成 ∵ PC⊥AB , AC=BC
∴PA=PB
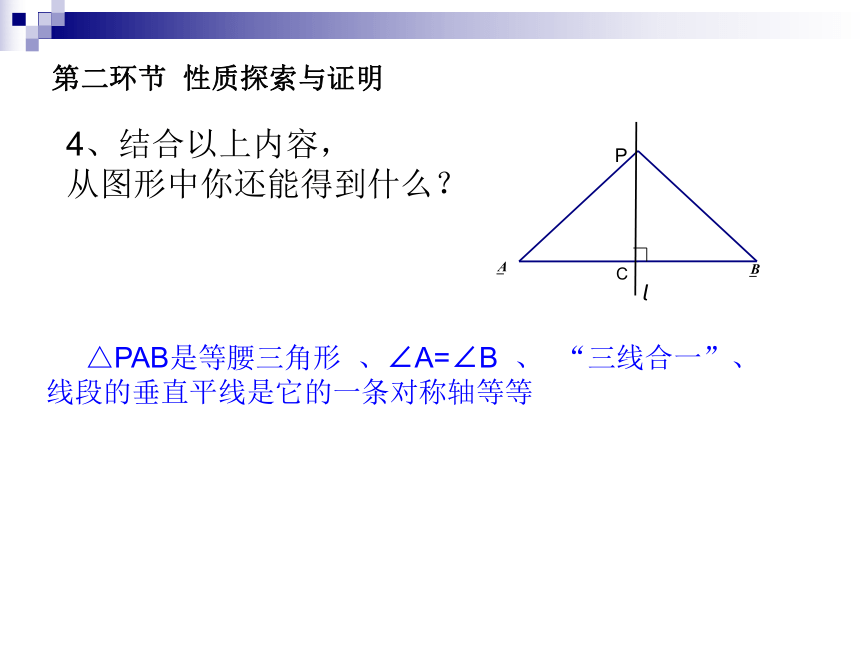
第二环节 性质探索与证明4、结合以上内容,
从图形中你还能得到什么? △PAB是等腰三角形 、∠A=∠B 、 “三线合一”、
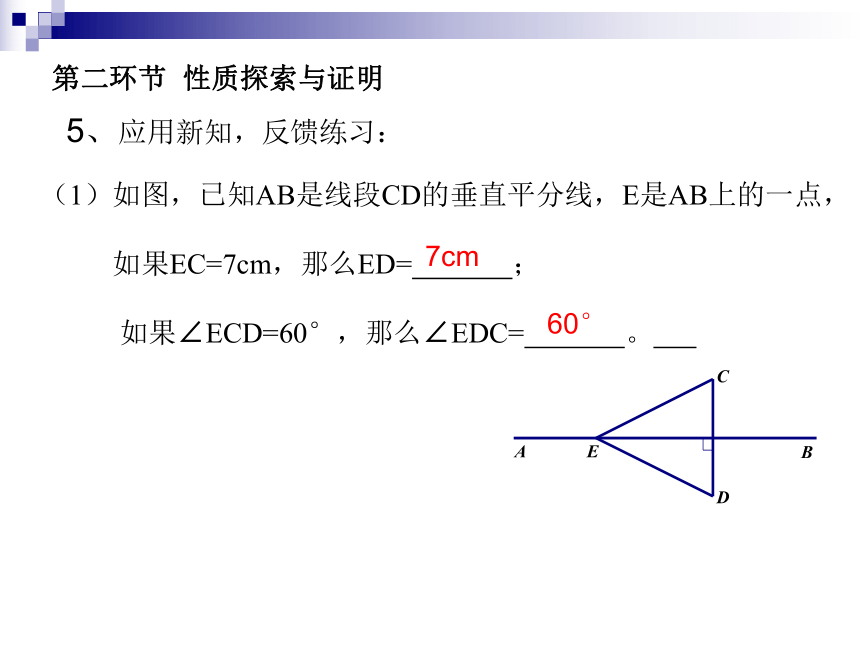
线段的垂直平线是它的一条对称轴等等5、应用新知,反馈练习:第二环节 性质探索与证明(1)如图,已知AB是线段CD的垂直平分线,E是AB上的一点,
如果EC=7cm,那么ED= ;
如果∠ECD=60°,那么∠EDC= 。 7cm60° 第二环节 性质探索与证明(2)已知:如图,AB是线段CD的垂直平分线,
E,F是线段AB上两点。
求证:∠ECF=∠EDF证明:
∵AB是线段CD的垂直平分线(已知)
∴ EC=ED, FC=FD (线段垂直平分线上的点到
这条线段两个端点的距离相等)
又 ∵EF=EF(公共边)
∴ ∠ECF= ∠ EDF(全等三角形的对应角相等) ∴ △ EFC ≌ △ EFD(SSS)第三环节 逆向思维,探索判定你能写出上面定理的逆命题吗?
如果 ,
那么 。
简写成:
。定理:线段垂直平分线上的点到这条线段两个端点的距离相等.一个点到一条线段两个端点的距离相等这个点在这条线段的垂直平分线上到一条线段两个端点的距离相等的点在这条线段的垂直平分线上第三环节 逆向思维,探索判定这是一个真命题吗?如果是真命题,请你加以证明已知: PA=PB.
如果一个点到一条线段两个端点的距离相等,
那么这个点在这条线段的垂直平分线上。求证:点P在线段AB的垂直平分线上. 线段垂直平分线的判定定理:
到一条线段两个端点距离相等的点,
在这条线段的垂直平分线上.4、∵PA=PB
∴点P在线段AB的垂直平分线上第三环节 逆向思维,探索判定用符号语言表示: 在这里只能确定这一个点P 在线段AB的垂直平分线上,
但不能说明经过P点的直线就是线段AB的垂直平分线
第四环节 实际应用,归纳提高:1、 例题:
已知:如图,在 △ABC 中,AB = AC,
O 是 △ABC 内一点,OB=OC.求证:直线 AO 垂直平分线段BC。.证明:
∵AB=AC (已知)
∴点A在线段BC的垂直平分线上(线段BC的垂直平分线判定定理)
∵OB=OC(已知)
∴点O在线段BC的垂直平分线上线段BC的垂直平分线判定定理)
∴直线 AO 垂直平分线段BC.(两点确 定一条直线)
归纳: 逆定理可以作为线段垂直平分线的判定,但必须是经过满足条件的( )个点的直 线才是线段的垂直平分线
两第四环节 实际应用,归纳提高:2、观察与思考 :
(1)观察下面用尺规作线段垂直平分线的步骤,
思考这种作法的依据。步骤一:分别以点A,B为圆心,以固定长(大于AB长的一半)
为半径画弧,两弧分别交于点E,F。
步骤二:过点E,F作直线,则直线EF就是线段AB的垂直平分线。
尺规作线段垂直平分线的依据: 。 到一条线段两个端点距离相等的
点,在这条线段的垂直平分线上.
3、引例中找码头地点的作法依据是: 如图,A、B表示两个仓库,要在A、B一侧的河岸边建造
一个码头,使它到两个仓库的距离相等,码头应建在什么位置?P.∴码头应建在P点理论依据是:第五环节:课堂小结,知识升华 通过这节课的学习你有哪些新的收获?还有哪些困惑? 1、线段垂直平分线的性质定理:
线段垂直平分线上的点到这条线段两个端点的距离相等.
2、线段垂直平分线的判定定理:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
3、用几何符号语言对线段垂直平分线的性质定理及其定理进行了证明.
4、逆定理作为线段垂直平分线的判定,但必须是经过满足条件的 ( 两 )个点的直线才是线段的垂直平分线.
5、通过对定理的证明体会理解证明的严谨性,并运用两个定理解决简单的实际问题.
等等--- 实际上线段的垂直平分线 可以看成是到线段两个端点距离相等的所有点的集合。
归纳总结 拓展延伸第六环节: 达标检测,知识反馈1、△ABC中,∠A=500,AB=AC,AB的垂直
平分线交AC于D则∠DBC的度数 .2、如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,
求BC的长。。解:∵ AB的垂直平分线DE
∴ EA=EB (线段垂直平分线性质定理)
∵ △BCE的周长=BC+EC+EB
∴ △BCE的周长=BC+EC+EA (等量代换)
∵ AC=EC+EA=27
∴ △BCE的周长=BC+AC=50
∴ BC=50-27=23
15 ° 3、如图,在△ABC中,AB=AC, ∠BAC=120°,AB的
垂直平分线交AB于点E,交BC于点F,连接AF,
求∠AFC的度数第六环节: 达标检测,知识反馈解:∵ AB=AC,∠BAC=120°
∴ ∠ B=∠C=(180°-120°)/2=30°(等边对等角)
∵ AB的垂直平分线EF
∴ FB=FA(线段垂直平分线性质定理)
∴ ∠1=∠ B=30° (等边对等角)
又∵ ∠AFC=∠1 +∠ B(三角形外角和定理)
∴ ∠AFC=30°+30°=60°
谢谢各位老师、同学们! 已知: PA=PB.
求证:点P在线段AB的垂直平分线上.
证明: 过点P作垂线PC⊥AB ,垂足为C
∴ PC是△PAB的高(作法知)
∵ PA=PB, (已知)
∴△PAB是等腰三角形
∴PC是△PAB的中线(三线合一)
∴ AC=BC,
∴PC是AB的垂直平分线
∴ P点在AB的垂直平分线PC上.(垂直平分线定义)第三环节 逆向思维,探索判定证法1第三环节 逆向思维,探索判定 证法2
已知: PA=PB.
求证:点P在线段AB的垂直平分线上.
证明:作△PAB的中线PC所在直线,
∴ PC是△PAB的中线 (作法知)
∵ PA=PB, (已知)
∴△PAB是等腰三角形
∴PC是△PAB的高(三线合一)
∴ PC⊥AB,
∴ P点在AB的垂直平分线PC上.(垂直平分线定义)第三环节 逆向思维,探索判定证法3
已知: PA=PB.
求证:点P在线段AB的垂直平分线上.
证明:作△PAB的角平分线PC所在直线,
∵ PA=PB,(已知)
又∵PC 是△PAB的角平分线 (作法知)
∴ AC=BC, PC⊥AB (等腰三角形 中“三线合一 ”)
∴ P点在AB的垂直平分线上.
一个码头,使它到两个仓库的距离相等,码头应建在什么位置?第一章 三角形的证明 1.3 线段的垂直平分线 –-(1)第二环节 性质探索与证明命题:
线段垂直平分线上的点到这条线段两个端点的距离相等 如果 ,
那么 . 分析命题的条件和结论一个点在线段的垂直平分线上这个点到这条线段两个端点的距离相等第二环节 性质探索与证明2、根据条件和结论写出已知和求证 已知:
求证: PA=PB直线 l ⊥AB,垂足是C, AC=BC,
P是l上的任意一点. ∵ l⊥AB (已知)
∴∠PCA=∠PCB=90°(垂直定义)
∵AC=BC(已知)
PC=PC(公共边)
∴△PCA≌△PCB(SAS)
∴PA=PB(全等三角形的对应边相等)_P.证明:第二环节 性质探索与证明3、 线段垂直平分线的性质定理:
线段垂直平分线上的点到这条线段两个端点的距离相等. 如图
∵l是AB的垂直平分线,点P是直线l上一点
用几何推理符号语言怎么表示性质定理?
∴PA=PB或写成 ∵ PC⊥AB , AC=BC
∴PA=PB
第二环节 性质探索与证明4、结合以上内容,
从图形中你还能得到什么? △PAB是等腰三角形 、∠A=∠B 、 “三线合一”、
线段的垂直平线是它的一条对称轴等等5、应用新知,反馈练习:第二环节 性质探索与证明(1)如图,已知AB是线段CD的垂直平分线,E是AB上的一点,
如果EC=7cm,那么ED= ;
如果∠ECD=60°,那么∠EDC= 。 7cm60° 第二环节 性质探索与证明(2)已知:如图,AB是线段CD的垂直平分线,
E,F是线段AB上两点。
求证:∠ECF=∠EDF证明:
∵AB是线段CD的垂直平分线(已知)
∴ EC=ED, FC=FD (线段垂直平分线上的点到
这条线段两个端点的距离相等)
又 ∵EF=EF(公共边)
∴ ∠ECF= ∠ EDF(全等三角形的对应角相等) ∴ △ EFC ≌ △ EFD(SSS)第三环节 逆向思维,探索判定你能写出上面定理的逆命题吗?
如果 ,
那么 。
简写成:
。定理:线段垂直平分线上的点到这条线段两个端点的距离相等.一个点到一条线段两个端点的距离相等这个点在这条线段的垂直平分线上到一条线段两个端点的距离相等的点在这条线段的垂直平分线上第三环节 逆向思维,探索判定这是一个真命题吗?如果是真命题,请你加以证明已知: PA=PB.
如果一个点到一条线段两个端点的距离相等,
那么这个点在这条线段的垂直平分线上。求证:点P在线段AB的垂直平分线上. 线段垂直平分线的判定定理:
到一条线段两个端点距离相等的点,
在这条线段的垂直平分线上.4、∵PA=PB
∴点P在线段AB的垂直平分线上第三环节 逆向思维,探索判定用符号语言表示: 在这里只能确定这一个点P 在线段AB的垂直平分线上,
但不能说明经过P点的直线就是线段AB的垂直平分线
第四环节 实际应用,归纳提高:1、 例题:
已知:如图,在 △ABC 中,AB = AC,
O 是 △ABC 内一点,OB=OC.求证:直线 AO 垂直平分线段BC。.证明:
∵AB=AC (已知)
∴点A在线段BC的垂直平分线上(线段BC的垂直平分线判定定理)
∵OB=OC(已知)
∴点O在线段BC的垂直平分线上线段BC的垂直平分线判定定理)
∴直线 AO 垂直平分线段BC.(两点确 定一条直线)
归纳: 逆定理可以作为线段垂直平分线的判定,但必须是经过满足条件的( )个点的直 线才是线段的垂直平分线
两第四环节 实际应用,归纳提高:2、观察与思考 :
(1)观察下面用尺规作线段垂直平分线的步骤,
思考这种作法的依据。步骤一:分别以点A,B为圆心,以固定长(大于AB长的一半)
为半径画弧,两弧分别交于点E,F。
步骤二:过点E,F作直线,则直线EF就是线段AB的垂直平分线。
尺规作线段垂直平分线的依据: 。 到一条线段两个端点距离相等的
点,在这条线段的垂直平分线上.
3、引例中找码头地点的作法依据是: 如图,A、B表示两个仓库,要在A、B一侧的河岸边建造
一个码头,使它到两个仓库的距离相等,码头应建在什么位置?P.∴码头应建在P点理论依据是:第五环节:课堂小结,知识升华 通过这节课的学习你有哪些新的收获?还有哪些困惑? 1、线段垂直平分线的性质定理:
线段垂直平分线上的点到这条线段两个端点的距离相等.
2、线段垂直平分线的判定定理:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
3、用几何符号语言对线段垂直平分线的性质定理及其定理进行了证明.
4、逆定理作为线段垂直平分线的判定,但必须是经过满足条件的 ( 两 )个点的直线才是线段的垂直平分线.
5、通过对定理的证明体会理解证明的严谨性,并运用两个定理解决简单的实际问题.
等等--- 实际上线段的垂直平分线 可以看成是到线段两个端点距离相等的所有点的集合。
归纳总结 拓展延伸第六环节: 达标检测,知识反馈1、△ABC中,∠A=500,AB=AC,AB的垂直
平分线交AC于D则∠DBC的度数 .2、如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,
求BC的长。。解:∵ AB的垂直平分线DE
∴ EA=EB (线段垂直平分线性质定理)
∵ △BCE的周长=BC+EC+EB
∴ △BCE的周长=BC+EC+EA (等量代换)
∵ AC=EC+EA=27
∴ △BCE的周长=BC+AC=50
∴ BC=50-27=23
15 ° 3、如图,在△ABC中,AB=AC, ∠BAC=120°,AB的
垂直平分线交AB于点E,交BC于点F,连接AF,
求∠AFC的度数第六环节: 达标检测,知识反馈解:∵ AB=AC,∠BAC=120°
∴ ∠ B=∠C=(180°-120°)/2=30°(等边对等角)
∵ AB的垂直平分线EF
∴ FB=FA(线段垂直平分线性质定理)
∴ ∠1=∠ B=30° (等边对等角)
又∵ ∠AFC=∠1 +∠ B(三角形外角和定理)
∴ ∠AFC=30°+30°=60°
谢谢各位老师、同学们! 已知: PA=PB.
求证:点P在线段AB的垂直平分线上.
证明: 过点P作垂线PC⊥AB ,垂足为C
∴ PC是△PAB的高(作法知)
∵ PA=PB, (已知)
∴△PAB是等腰三角形
∴PC是△PAB的中线(三线合一)
∴ AC=BC,
∴PC是AB的垂直平分线
∴ P点在AB的垂直平分线PC上.(垂直平分线定义)第三环节 逆向思维,探索判定证法1第三环节 逆向思维,探索判定 证法2
已知: PA=PB.
求证:点P在线段AB的垂直平分线上.
证明:作△PAB的中线PC所在直线,
∴ PC是△PAB的中线 (作法知)
∵ PA=PB, (已知)
∴△PAB是等腰三角形
∴PC是△PAB的高(三线合一)
∴ PC⊥AB,
∴ P点在AB的垂直平分线PC上.(垂直平分线定义)第三环节 逆向思维,探索判定证法3
已知: PA=PB.
求证:点P在线段AB的垂直平分线上.
证明:作△PAB的角平分线PC所在直线,
∵ PA=PB,(已知)
又∵PC 是△PAB的角平分线 (作法知)
∴ AC=BC, PC⊥AB (等腰三角形 中“三线合一 ”)
∴ P点在AB的垂直平分线上.
