五年级数学下册课件 旋转变换(沪教版)
文档属性
| 名称 | 五年级数学下册课件 旋转变换(沪教版) |  | |
| 格式 | rar | ||
| 文件大小 | 412.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-05 19:27:00 | ||
图片预览







文档简介
课件21张PPT。沪教版五年级数学下册旋转变换教学目标让同学们进一步认识图形的旋转,认识按顺时针或逆时针方向旋转的含义,能在方格纸上把简单图形旋转。
让同学们通过学习活动,进一步增强空间观念,发展形象思维。
让同学们在认识旋转的过程中,产生对图形与变化的兴趣,并进一步感受旋转在生活里的应用。 上面的运动现象中,有哪些共同的特点? 由一个图形改变为另一个图形,在改变的过程
中,原图形上的所有点都绕 ,按
,转动 ,这样的图形
改变叫做图形的旋转变换,简称旋转。
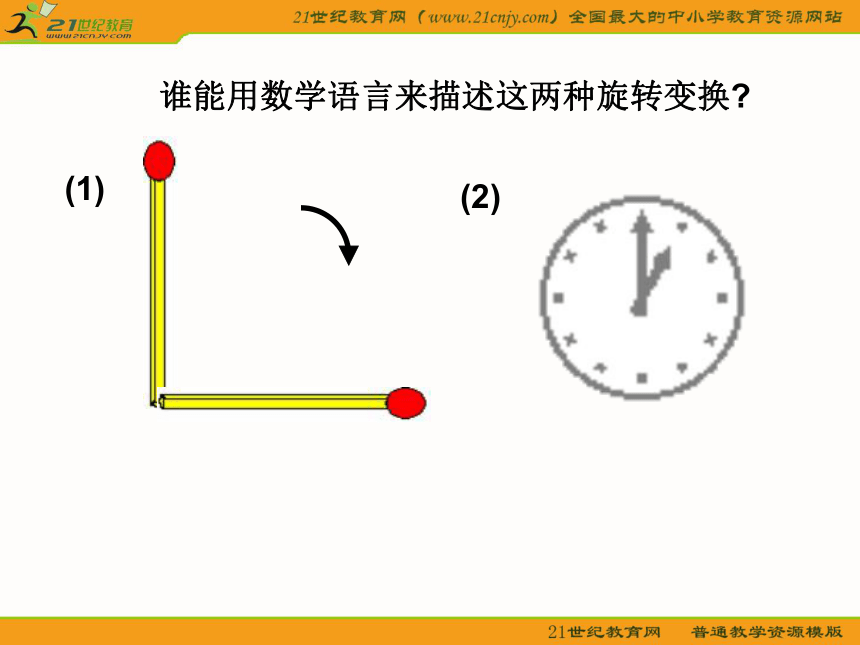
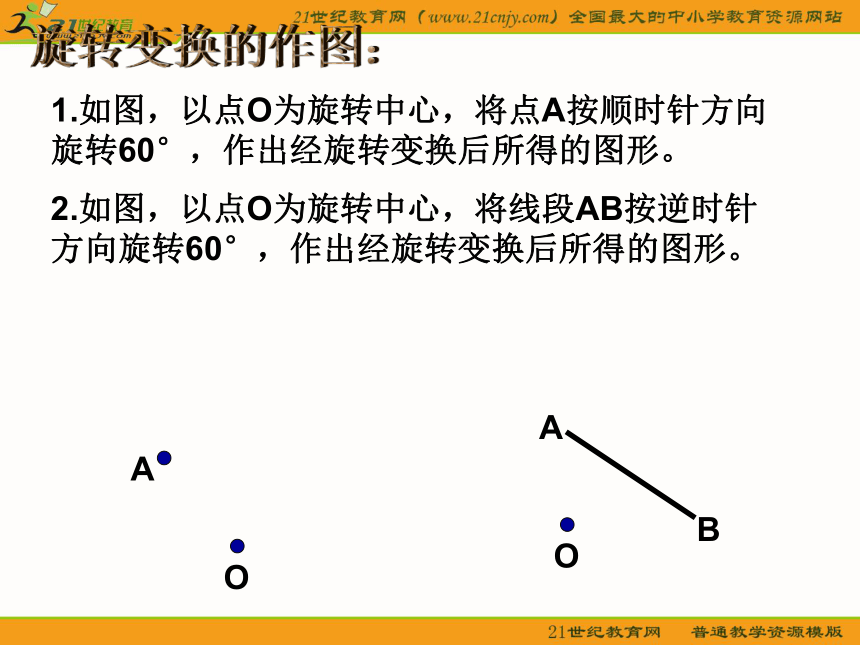
这个固定的点叫做旋转中心。一个固定的点同一个方向同一个角度叙述一个旋转变换要注意旋转变换的三个要素:1.旋转中心;2.旋转的方向;3.旋转的角度。什么是旋转变换呢?谁能用数学语言来描述这两种旋转变换?(1)(2)旋转变换的作图:1.如图,以点O为旋转中心,将点A按顺时针方向
旋转60°,作出经旋转变换后所得的图形。2.如图,以点O为旋转中心,将线段AB按逆时针
方向旋转60°,作出经旋转变换后所得的图形。OAABO旋转变换的作图:例1 如图,O是△ABC外一点,以点O为旋转中心,
将△ABC按逆时针方向旋转30°,作出经旋转
变换后的像。.议一议:
如图所示,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:1.旋转中心是什么?BACODEF2.经过旋转,点A,B
分别移动到什么位置?3.AO与DO的长有什么关
系?BO与EO呢?4.∠AOD与∠BOE有什
么大小关系?
旋转的基本性质
(1)旋转不改变图形的形状和大小。
(2)对应点到旋转中心的距离相等,对应点与旋转中心的连线所成的角度等于旋转的角度。 由上面的问题回答可知,经旋转变换所得的图形和原图形在形状和大小上有什么关系?1.如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,点 是旋转中心,旋转了 度
点B的对应点是点 ;线段AB的对应线段是 ;∠ABC的对应角是 。A45°DAD∠ADEABC.ODEF 2.由演示可知:△ABC由△DEF关于点O旋转变换得到,请你找出图中关于点O的对称点和关于点O的对称线段。 例2 如图,△ ABC绕C点旋转后,顶点A的对应点为点D。试确定顶点B对应点的位置,以及旋转后的三角形。解:分析:假设顶点B的对应点为点E,则∠BCE,∠ACD都是旋转角,且CE=CB,CD=CA。(3)在射线CE上截取CE=CB。(2)如图,以CB为一边作∠BCE,
使得∠BCE= ∠ACD。(4)连接DE。△DEC就是△ABC绕C点旋转变换后的像。ABDC(1)连接CD。·练习:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?1.相同:都是一种运动;运动前 后不改变图形的形状和大小BACO2.不同
请思考平移和旋转的异同点?做一做:
在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.ACBDEFGH 如下图,在方格纸上作出“小旗子”绕 O点按顺时针方向旋转90o后的图案,并简述理由。随堂练习:
本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?现在你能很快地找到点
E的对应点F吗?认真观察风车OA__OBOC__OD观察一对对应点与其旋转中心有何位置和数量关系?
让同学们通过学习活动,进一步增强空间观念,发展形象思维。
让同学们在认识旋转的过程中,产生对图形与变化的兴趣,并进一步感受旋转在生活里的应用。 上面的运动现象中,有哪些共同的特点? 由一个图形改变为另一个图形,在改变的过程
中,原图形上的所有点都绕 ,按
,转动 ,这样的图形
改变叫做图形的旋转变换,简称旋转。
这个固定的点叫做旋转中心。一个固定的点同一个方向同一个角度叙述一个旋转变换要注意旋转变换的三个要素:1.旋转中心;2.旋转的方向;3.旋转的角度。什么是旋转变换呢?谁能用数学语言来描述这两种旋转变换?(1)(2)旋转变换的作图:1.如图,以点O为旋转中心,将点A按顺时针方向
旋转60°,作出经旋转变换后所得的图形。2.如图,以点O为旋转中心,将线段AB按逆时针
方向旋转60°,作出经旋转变换后所得的图形。OAABO旋转变换的作图:例1 如图,O是△ABC外一点,以点O为旋转中心,
将△ABC按逆时针方向旋转30°,作出经旋转
变换后的像。.议一议:
如图所示,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:1.旋转中心是什么?BACODEF2.经过旋转,点A,B
分别移动到什么位置?3.AO与DO的长有什么关
系?BO与EO呢?4.∠AOD与∠BOE有什
么大小关系?
旋转的基本性质
(1)旋转不改变图形的形状和大小。
(2)对应点到旋转中心的距离相等,对应点与旋转中心的连线所成的角度等于旋转的角度。 由上面的问题回答可知,经旋转变换所得的图形和原图形在形状和大小上有什么关系?1.如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,点 是旋转中心,旋转了 度
点B的对应点是点 ;线段AB的对应线段是 ;∠ABC的对应角是 。A45°DAD∠ADEABC.ODEF 2.由演示可知:△ABC由△DEF关于点O旋转变换得到,请你找出图中关于点O的对称点和关于点O的对称线段。 例2 如图,△ ABC绕C点旋转后,顶点A的对应点为点D。试确定顶点B对应点的位置,以及旋转后的三角形。解:分析:假设顶点B的对应点为点E,则∠BCE,∠ACD都是旋转角,且CE=CB,CD=CA。(3)在射线CE上截取CE=CB。(2)如图,以CB为一边作∠BCE,
使得∠BCE= ∠ACD。(4)连接DE。△DEC就是△ABC绕C点旋转变换后的像。ABDC(1)连接CD。·练习:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?1.相同:都是一种运动;运动前 后不改变图形的形状和大小BACO2.不同
请思考平移和旋转的异同点?做一做:
在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.ACBDEFGH 如下图,在方格纸上作出“小旗子”绕 O点按顺时针方向旋转90o后的图案,并简述理由。随堂练习:
本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?现在你能很快地找到点
E的对应点F吗?认真观察风车OA__OBOC__OD观察一对对应点与其旋转中心有何位置和数量关系?
