2016年青岛版七年级数学上册 第三章 有理数的运算 测试题(含解析)
文档属性
| 名称 | 2016年青岛版七年级数学上册 第三章 有理数的运算 测试题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 167.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-22 15:28:48 | ||
图片预览


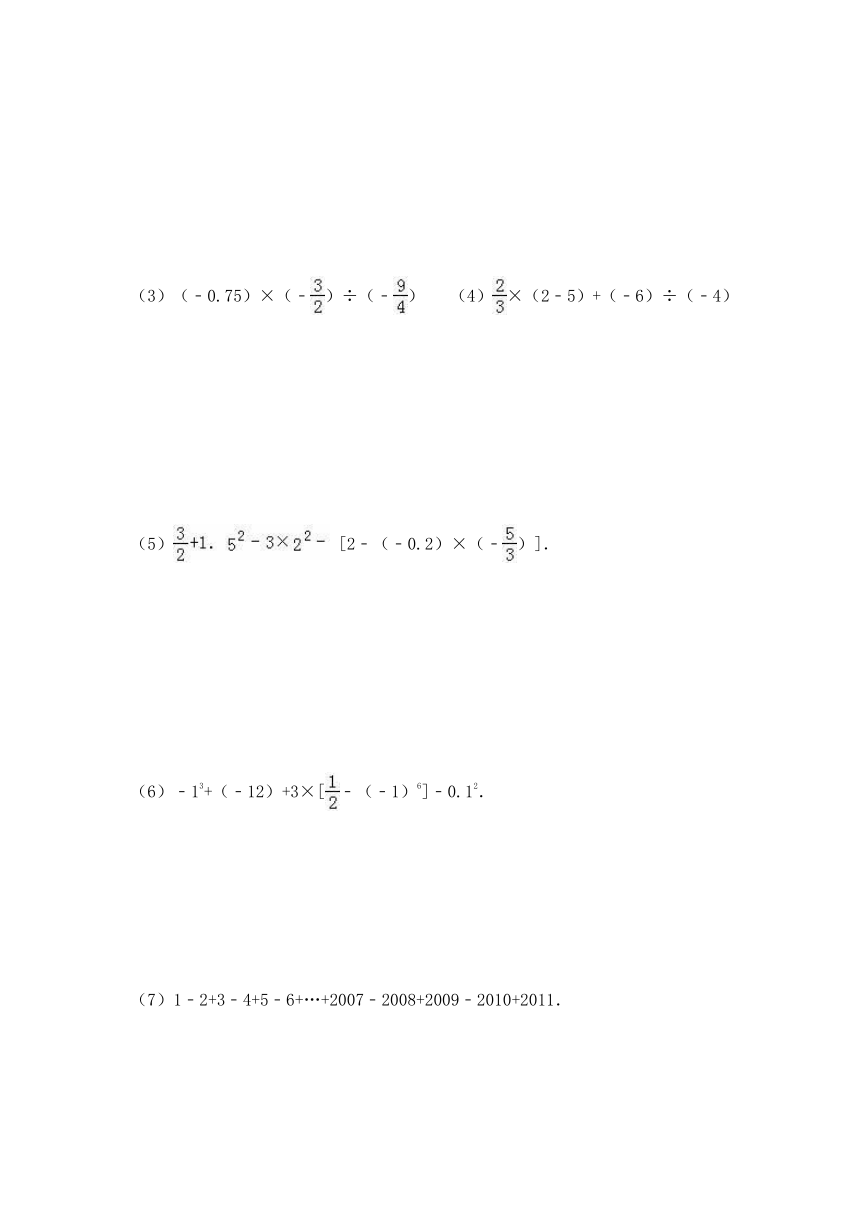


文档简介
七年级数学第三章测试题
一.选择题(共12小题)
1.﹣0.25的倒数是( )
A.
B.4
C.﹣4
D.﹣5
2.-|﹣|的倒数是( )
A.
B.﹣
C.2
D.﹣2
3.a与互为相反数,则a的倒数是( )
A.
B.
C.3
D.﹣3
4.如图,数轴的单位长度为1,如果P,Q表示的数互为相反数,那么图中的4个点中,哪一个点表示的数的平方值最大( )
A.P
B.R
C.Q
D.T
5.下列说法正确的是( )
A.绝对值是本身的数是正数
B.倒数是本身的数是±1
C.平方是它本身的数是0
D.立方等于本身的数是±1
定义运算a b=a(1﹣b),下面给出的四个结论中正确的是( )
A.2 (﹣2)=﹣4
B.a b=b a
C.(﹣2) 2=2
D.若a b=0,则a=0
7.下列说法不正确的是( )
A.一个数(不为0)与它的倒数之积是1
B.一个数与它的相反数之和为0
C.两个数的商为﹣1,这两个数互为相反数
D.两个数的积为1,这两个数互为相反数
8.已知x<0,y>0,且|x|>|y|,则x+y的值是( )
A.非负数
B.负数
C.正数
D.0
9.在进行异号的两个有理数加法运算时,用到下面的一些操作:
①将绝对值较大的有理数的符号作为结果的符号并记住
②将记住的符号和绝对值的差一起作为最终的计算结果
③用较大的绝对值减去较小的绝对值
④求两个有理数的绝对值
⑤比较两个绝对值的大小
其中操作顺序正确的步骤是( )
A.①②③④⑤
B.④⑤③②①
C.①⑤③④②
D.④⑤①③②
10.古希腊数学家帕普斯是丢潘图是最得意的一个学生,有一天他向老师请教一个问题:有4个数,把其中每3个相加,其和分别是22,24,27,20,则这个四个数是( )
A.3,8,9,10
B.10,7,3,12
C.9,7,4,11
D.9,6,5,11
11.如果|a+2|和(b﹣1)2互为相反数,那么(a+b)2015的值是( )
A.﹣2015
B.2015
C.﹣1
D.1
12.如图是一个数值运算的程序,若输出的y值为3,则输入的x值为( )
A.3.5
B.﹣3.5
C.7
D.﹣7
二.填空题(共6小题)
13.绝对值大于2.6而小于5.3的所有负整数之和为______.
14.把(+5)﹣(﹣7)+(﹣23)﹣(+6)写成省略括号的和的形式为______.
15.已知a=255,b=344,c=433,则a,b,c的大小关系为______.
16.已知|x|=2,|y|=5,且x>y,则x+y=______.
17.若ab<0,则的值为______.
18.若“!”是一种数学运算符号,并且:1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则=______.
三.解答题(共9小题)
19.计算题:
(1)(﹣12)×(﹣)
(2)
﹣2.
(3)(﹣0.75)×(﹣)÷(﹣)
(4)×(2﹣5)+(﹣6)÷(﹣4)
(5)
[2﹣(﹣0.2)×(﹣)].
(6)﹣13+(﹣12)+3×[﹣(﹣1)6]﹣0.12.
(7)1﹣2+3﹣4+5﹣6+…+2007﹣2008+2009﹣2010+2011.
20.
请你参考黑板中老师的讲解,用运算律简便计算:
(1)999×(﹣15)
(2)999×118+999×(﹣)﹣999×18.
21.阅读材料,求值:1+2+22+23+24+…+22015.
解:设S=1+2+22+23+24+…+22015,将等式两边同时乘以2得:
2S=2+22+23+24+…+22015+22016
将下式减去上式得2S﹣S=22016﹣1
即S=1+2+22+23+24+…+22015=22016﹣1
请你仿照此法计算:
(1)1+2+22+23+…+210
(2)1+3+32+33+34+…+3n(其中n为正整数)
22.观察下列各等式,并回答问题:
=1﹣;
=﹣;
=﹣;
=﹣;…
(1)填空:
=______(n是正整数)
(2)计算:
++++…+=______.
(3)计算:
++++…+=______.
(4)求++++…+的值.
23.在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的“探究”
【提出问题】三个有理数a、b、c满足abc>0,求的值.
【解决问题】
解:由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c都是正数,即a>0,b>0,c>0时,
则:
==1+1+3;②当a,b,c有一个为正数,另两个为负数时,设a>0,b<0,c<0,
则:
==1+(﹣1)+(﹣1)=﹣1
所以的值为3或﹣1.
【探究】请根据上面的解题思路解答下面的问题:
(1)三个有理数a,b,c满足abc<0,求的值;
(2)已知|a|=3,|b|=1,且a<b,求a+b的值.
2016年09月23日1526467859的初中数学组卷
参考答案与试题解析
一.选择题(共12小题)
1.(2016 陕西校级三模)﹣0.25的倒数是( )
A.
B.4
C.﹣4
D.﹣5
【分析】根据倒数的定义回答即可.
【解答】解:∵﹣0.25×(﹣4)=1,
∴﹣0.25的倒数是﹣4.
故选;C.
【点评】本题主要考查的是倒数的定义,掌握倒数的定义是解题的关键.
2.(2015 攀枝花模拟)|﹣|的倒数是( )
A.
B.﹣
C.2
D.﹣2
【分析】首先根据绝对值的求法,求出|﹣|的大小;然后根据求一个数的倒数的方法,求出|﹣|的倒数是多少即可.
【解答】解:∵|﹣|=,1÷,
∴,
∴|﹣|的倒数是2.
故选:C.
【点评】(1)此题主要考查了倒数的含义和求法,要熟练掌握,解答此题的关键是要明确:乘积是1的两个数互为倒数.
(2)此题还考查了绝对值的非负性质和求法,要熟练掌握.
3.(2016 威海二模)a与互为相反数,则a的倒数是( )
A.
B.
C.3
D.﹣3
【分析】依据相反数的定义求得a的值,然后再依据倒数的定义求解即可.
【解答】解:∵﹣与互为相反数,
∴a=﹣.
∵﹣的倒数是﹣3,
∴a的倒数是﹣3.
故选:D.
【点评】本题主要考查的是相反数、倒数的定义,掌握相关定义是解题的关键.
4.(2015 杭州模拟)如图,数轴的单位长度为1,如果P,Q表示的数互为相反数,那么图中的4个点中,哪一个点表示的数的平方值最大( )
A.P
B.R
C.Q
D.T
【分析】由于点P,Q表示的数是互为相反数,根据相反数的定义易得点P表示的数为﹣2.5,Q点表示的数为2.5,则点R表示的数为﹣0.5,T点表示的数为3.5,然后求出各数的平方即可确定正确答案
【解答】解:∵点P,Q表示的数是互为相反数,
而PQ=5,
∴点P表示的数为﹣2.5,B点表示的数为2.5,
∴点R表示的数为﹣0.5,T点表示的数为3.5,
∵2.52=6.25,(﹣2.5)2=6.25,(﹣0.5)2=0.25,3.52=12.25,
∴表示的数的平方值最大的点是T.
故选D.
【点评】本题考查了数轴:数轴的三要素(原点、单位长度和正方向);数轴上左边的点表示的数比右边点表示的数大,也考查了平方与相反数,用几何方法借助数轴来求解,非常直观,且不容易遗漏,体现了数形结合的优点.
5.(2015秋 邵阳校级期末)下列说法正确的是( )
A.绝对值是本身的数是正数
B.倒数是本身的数是±1
C.平方是它本身的数是0
D.立方等于本身的数是±1
【分析】根据绝对值的性质、倒数的定义、有理数的乘方法则判断即可.
【解答】解:A、绝对值是本身的数是正数和0,故A错误;
B、倒数是本身的数是±1,故B正确;
C、平方是它本身的数是0和1,故C错误;
D、立方等于本身的数是±1和0,故D错误.
故选:B.
【点评】本题主要考查的是绝对值的性质、倒数的定义、有理数的乘方,利用0,1,﹣1的特殊性进行判断是解题的关键.
6.(2015 新市区二模)定义运算a b=a(1﹣b),下面给出的关于这种运算的四个结论中正确的是( )
A.2 (﹣2)=﹣4
B.a b=b a
C.(﹣2) 2=2
D.若a b=0,则a=0
【分析】A:根据新运算a b=a(1﹣b),求出2 (﹣2)的值是多少,即可判断出2 (﹣2)=﹣4是否正确.
B:根据新运算a b=a(1﹣b),求出a b、b a的值各是多少,即可判断出a b=b a是否正确.
C:根据新运算a b=a(1﹣b),求出(﹣2) 2的值是多少,即可判断出(﹣2) 2=2是否正确.
D:根据a b=0,可得a(1﹣b)=0,所以a=0或b=1,据此判断即可.
【解答】解:∵2 (﹣2)=2×[1﹣(﹣2)]=2×3=6,
∴选项A不正确;
∵a b=a(1﹣b),b a=b(1﹣a),
∴a b=b a只有在a=b时成立,
∴选项B不正确;
∵(﹣2) 2=(﹣2)×(1﹣2)=(﹣2)×(﹣1)=2,
∴选项C正确;
∵a b=0,
∴a(1﹣b)=0,
∴a=0或b=1
∴选项D不正确.
故选:C.
【点评】(1)此题主要考查了有理数的混合运算,要熟练掌握,解答此题的关键是要明确:①有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.②进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
(2)此题还考查了对新运算“ ”的理解和掌握,解答此题的关键是要明确:a b=a(1﹣b).
7.(2015秋 重庆期末)下列说法不正确的是( )
A.一个数(不为0)与它的倒数之积是1
B.一个数与它的相反数之和为0
C.两个数的商为﹣1,这两个数互为相反数
D.两个数的积为1,这两个数互为相反数
【分析】根据倒数、相反数、有理数的乘法和除法法则判断即可.
【解答】解:A、根据倒数的定义可知A正确,与要求不符;
B、互为相反数的两数之和为0,故B正确,与要求不符;
C、根据有理数的除法法则可知C正确,与要求不符;
D、两个数的积为1则两数互为倒数,故D错误,与要求相符.
故选:D.
【点评】本题主要考查的是倒数、相反数的定义,掌握相关法则是解题的关键.
8.(2015秋 邵阳校级期末)已知x<0,y>0,且|x|>|y|,则x+y的值是( )
A.非负数
B.负数
C.正数
D.0
【分析】绝对值不相等的异号两数相加取绝对值较大的加数的符号.
【解答】解:∵|x|>|y|,
∴x+y的符号与x的符号一致.
∵x<0,
∴x+y<0.
故选:B.
【点评】本题主要考查的是有理数的加法,判断出和的符号与x的符号一致是解题的关键.
9.(2015秋 丰台区期末)在进行异号的两个有理数加法运算时,用到下面的一些操作:
①将绝对值较大的有理数的符号作为结果的符号并记住
②将记住的符号和绝对值的差一起作为最终的计算结果
③用较大的绝对值减去较小的绝对值
④求两个有理数的绝对值
⑤比较两个绝对值的大小
其中操作顺序正确的步骤是( )
A.①②③④⑤
B.④⑤③②①
C.①⑤③④②
D.④⑤①③②
【分析】依据有理数的加法法则进行判断即可.
【解答】解;在进行异号的两个有理数加法运算时,应先求两个有理数的绝对值,然后比较两个绝对值的大小,接下来将绝对值较大的有理数的符号作为结果的符号并记住,然后用较大的绝对值减去较小的绝对值,最后将记住的符号和绝对值的差一起作为最终的计算结果,故正确的顺序是④⑤①③②.
故选:D.
【点评】本题主要考查的是有理数的加法,掌握有理数的加法法则是解题的关键.
10.(2015秋 牡丹区期末)古希腊数学家帕普斯是丢潘图是最得意的一个学生,有一天他向老师请教一个问题:有4个数,把其中每3个相加,其和分别是22,24,27,20,则这个四个数是( )
A.3,8,9,10
B.10,7,3,12
C.9,7,4,11
D.9,6,5,11
【分析】设出4个数,按照题意列出方程组,即可得出结论.
【解答】解:设a、b、c、d为这4个数,且a>b>c>d,
则有,
解得:a=11,b=9,c=7,d=4.
故选C.
【点评】本题考查的有理数的加法,解题的关键是按大小顺序设出4个数,联立方程组得出结论.
11.(2015秋 宜宾期末)如果|a+2|和(b﹣1)2互为相反数,那么(a+b)2015的值是( )
A.﹣2015
B.2015
C.﹣1
D.1
【分析】根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.
【解答】解:由题意得,|a+2|+(b﹣1)2,=0,
则|a+2|=0,(b﹣1)2=0,
解得,a=﹣2,b=1,
∴(a+b)2015=﹣1,
故选:C.
【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.
12.(2015秋 南京期末)如图是一个数值运算的程序,若输出的y值为3,则输入的x值为( )
A.3.5
B.﹣3.5
C.7
D.﹣7
【分析】由题意可得[(﹣x)﹣1]÷2=y,然后令y=3即可得到输入的x的值.
【解答】解:由题意可得,
[(﹣x)﹣1]÷2=y,
当y=3时,
[(﹣x)﹣1]÷2=3,
解得,x=﹣7,
故选D.
【点评】本题考查有理数的混合运算,解题的关键是明确题意,根据题意可以列出相应的关系式.
二.选择题(共6小题)
13.(2015秋 邵阳校级期末)绝对值大于2.6而小于5.3的所有负整数之和为 ﹣12 .
【分析】先找出符合条件的数,然后再求得它们的和即可.
【解答】解:绝对值大于2.6而小于5.3的负整数有:﹣3、﹣4、﹣5.
﹣3+(﹣4)+(﹣5)=﹣12.
故答案为:﹣12.
【点评】本题主要考查的是绝对值、有理数的加法,找出符合条件的数是解题的关键.
14.(2015秋 衡阳县期末)把(+5)﹣(﹣7)+(﹣23)﹣(+6)写成省略括号的和的形式为 5+7﹣23﹣6 .
【分析】先把减法都转化成加法,然后省略括号和加号即可.
【解答】解:(+5)﹣(﹣7)+(﹣23)﹣(+6)=(+5)+(+7)+(﹣23)+(﹣6),
则写成省略括号的和的形式为:5+7﹣23﹣6.
故答案为:5+7﹣23﹣6.
【点评】本题考查的是写成省略括号的和的形式,掌握有理数减法法则,把减法都转化成加法,并写成省略括号的和的形式是解题的关键.
15.(2015春 江都区校级月考)已知a=255,b=344,c=433,则a,b,c的大小关系为 a<c<b .
【分析】根据幂运算的性质,及它们的指数相同,只需比较它们的底数的大小,底数大的就大.
【解答】解:a=255=(25)11=3211,
b=344=(34)11=8111,
c=433=(43)11=6411,
则b>c>a.
【点评】此题要熟练运用幂运算的性质把它们变成相同的指数,然后根据底数的大小比较两个数的大小.
16.(2015秋 河东区校级期中)已知|x|=2,|y|=5,且x>y,则x+y= ﹣3或﹣7 .
【分析】先求得x、y的值,然后根据x>y分类计算即可.
【解答】解:∵|x|=2,|y|=5,
∴x=±2,y=±5.
∵x>y,
∴x=2,y=﹣5或x=﹣2,y=﹣5.
∴x+y=2+(﹣5)=﹣3或x+y=﹣2+(﹣5)=﹣7.
故答案为:﹣3或﹣7.
【点评】本题主要考查的是有理数的加法、绝对值的性质,分类讨论是解题的关键.
17.(2015秋 诸暨市校级期中)若ab<0,则的值为 1 .
【分析】由ab<0,可知a、b异号,然后利用有理数的乘法法则化简即可.
【解答】解:∵ab<0,
∴a、b异号.
∴=0.
∴=0+1=1.
故答案为:1.
【点评】本题主要考查的是绝对值的性质、有理数的除法,根据题意得出a、b异号是解题的关键.
18.(2015秋 桐乡市校级期中)若“!”是一种数学运算符号,并且:1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则= 2550 .
【分析】根据运算符号“!”的意义,然后列式计算即可.
【解答】解:
==51×50=2550.
故答案为:2550.
【点评】本题主要考查的是有理数的乘法和除法,利用定义运算是解题的关键.
三.选择题(共9小题)
19.(2015秋 房山区期末)计算:.
【分析】依据乘法的分配律计算即可.
【解答】解:原式=﹣36×﹣36×+36×
=﹣24﹣27+3
=﹣48.
【点评】本题主要考查的是有理数的乘法,依据乘法的分配律进行简便计算是解题的关键.
20.(2015秋 大石桥市期末)计算:
(1)(﹣12)×(﹣)
(2)﹣2.
【分析】(1)根据乘法的分配律进行计算即可;
(2)根据幂的乘方、绝对值、有理数的乘除和加减进行计算即可.
【解答】解:(1)(﹣12)×(﹣)
=(﹣12)×+(﹣12)×
=9+7﹣10
=6;
(2)﹣2
=﹣4+3+24×
=﹣4+3﹣
=﹣.
【点评】本题考查有理数的混合运算,解题的关键是明确乘法的分配律和有理数的混合运算的方法.
21.(2015秋 淮安校级期末)计算下列各题:
(1)﹣3﹣4+19﹣11
(2)(﹣0.75)×(﹣)÷(﹣)
(3)
[2﹣(﹣0.2)×(﹣)].
【分析】(1)根据有理数的加法和减法进行计算即可;
(2)根据有理数的乘法和加法进行计算即可;
(3)根据有理数混合运算的方法进行计算即可.
【解答】解:(1)﹣3﹣4+19﹣11
=﹣3﹣4﹣11+19
=1;
(2)(﹣0.75)×(﹣)÷(﹣)
=﹣××
=﹣;
(3)
[2﹣(﹣0.2)×(﹣)]
=
=
=
=.
【点评】本题考查有理数的混合运算,解题的关键是明确有理数混合运算的方法.
22.(2015秋 海口期末)计算:
(1)×(2﹣5)+(﹣6)÷(﹣4)
(2)(﹣+﹣)×(﹣48)
(3)﹣13+(﹣12)+3×[﹣(﹣1)6]﹣0.12.
【分析】(1)根据有理数的乘法、除法和加法进行计算即可;
(2)根据乘法的分配律进行计算即可;
(3)根据幂的乘方、有理数的乘法、加法和减法进行计算即可.
【解答】解:(1)×(2﹣5)+(﹣6)÷(﹣4)
=
=﹣2+
=﹣;
(2)(﹣+﹣)×(﹣48)
=
=8﹣36+12
=﹣16;
(3)﹣13+(﹣12)+3×[﹣(﹣1)6]﹣0.12
=﹣1+(﹣12)+3×
=﹣1+(﹣12)+3×
=﹣1+(﹣12)﹣1.5﹣0.01
=﹣14.51.
【点评】本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.
23.(2015秋 东港市期末)计算
(1)﹣10﹣8÷(﹣2)×(﹣)
(2)﹣22+(﹣3)2÷(﹣)+|﹣4|×(﹣1)2015.
【分析】(1)根据有理数的乘除法和减法进行计算即可;
(2)根据有理数的加减乘除进行计算即可.
【解答】解:(1)﹣10﹣8÷(﹣2)×(﹣)
=﹣10﹣8×
=﹣10﹣2
=﹣12;
(2)﹣22+(﹣3)2÷(﹣)+|﹣4|×(﹣1)2015
=﹣4+9×+4×(﹣1)
=﹣4﹣2﹣4
=﹣10.
【点评】本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.
24.(2016春 启东市月考)计算:1﹣2+3﹣4+5﹣6+…+2007﹣2008+2009﹣2010+2011.
【分析】根据算式的特征,应用加法结合律,分别求出﹣2+3、﹣4+5、﹣6+7、…、﹣2006+2007、﹣2008+2009、﹣2010+2011的值各是多少,进而求出算式1﹣2+3﹣4+5﹣6+…+2007﹣2008+2009﹣2010+2011的值是多少即可.
【解答】解:1﹣2+3﹣4+5﹣6+…+2007﹣2008+2009﹣2010+2011
=1+(﹣2+3)+(﹣4+5)+(﹣6+7)+…+(﹣2006+2007)+(﹣2008+2009)+(﹣2010+2011)
=1+
=1+1005
=1006
【点评】此题主要考查了有理数的加减混合运算,要熟练掌握,解答此题的关键是应用加法结合律,分别求出﹣2+3、﹣4+5、﹣6+7、…、﹣2006+2007、﹣2008+2009、﹣2010+2011的值各是多少.
25.(2016 河北)
请你参考黑板中老师的讲解,用运算律简便计算:
(1)999×(﹣15)
(2)999×118+999×(﹣)﹣999×18.
【分析】(1)将式子变形为(1000﹣1)×(﹣15),再根据乘法分配律计算即可求解;
(2)根据乘法分配律计算即可求解.
【解答】解:(1)999×(﹣15)
=(1000﹣1)×(﹣15)
=1000×(﹣15)+15
=﹣15000+15
=﹣14985;
(2)999×118+999×(﹣)﹣999×18
=999×(118﹣﹣18)
=999×100
=99900
【点评】考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.(2)进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
26.(2015秋 淮阴区期末)阅读材料,求值:1+2+22+23+24+…+22015.
解:设S=1+2+22+23+24+…+22015,将等式两边同时乘以2得:
2S=2+22+23+24+…+22015+22016
将下式减去上式得2S﹣S=22016﹣1
即S=1+2+22+23+24+…+22015=22016﹣1
请你仿照此法计算:
(1)1+2+22+23+…+210
(2)1+3+32+33+34+…+3n(其中n为正整数)
【分析】(1)根据题目中材料可以得到用类比的方法得到1+2+22+23+…+210的值;
(2)根据题目中材料可以得到用类比的方法得到1+3+32+33+34+…+3n的值.
【解答】解:(1)设S=1+2+22+23+24+…+210,
将等式两边同时乘以2,得
2S=2+22+23+24+…+211
将下式减去上式,得
2S﹣S=211﹣1
即S=1+2+22+23+24+…+210=211﹣1;
(2)设S=1+3+32+33+34+…+3n,
将等式两边同时乘以3,得
3S=3+32+33+34+…+3n+1,
将下式减去上式,得
3S﹣S=3n+1﹣1
即2S=3n+1﹣1
得S=1+3+32+33+34+…+3n=.
【点评】本题考查有理数的乘方,解题的关键是明确题意,运用题目中的解题方法,运用类比的数学思想解答问题.
四.解答题(共2小题)
27.(2015秋 重庆校级期中)观察下列各等式,并回答问题:
=1﹣;
=﹣;
=﹣;
=﹣;…
(1)填空:
= ﹣ (n是正整数)
(2)计算:
++++…+= .
(3)计算:
++++…+= .
(4)求++++…+的值.
【分析】(1)根据题意确定出拆项规律,写出第n个式子即可;
(2)根据拆项规律,先拆项再抵消写即可求解;
(3)根据拆项规律,先拆项再抵消写即可求解;
(4)根据拆项规律,先拆项再抵消写即可求解.
【解答】解:(1)=﹣(n是正整数)
(2)++++…+
=1﹣+﹣+…+﹣
=1﹣
=.
(3)++++…+
=1﹣+﹣+…+﹣
=1﹣
=.
(4)++++…+
=×(1﹣+﹣+﹣+…+﹣)
=×(1﹣)
=×
=.
故答案为:(1)﹣;
(2);(3).
【点评】考查了有理数的混合运算,(4)的关键是将式子变形为×(1﹣+﹣+﹣+…+﹣)进行计算.
28.(2015秋 烟台期中)在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的“探究”
【提出问题】三个有理数a、b、c满足abc>0,求的值.
【解决问题】
解:由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c都是正数,即a>0,b>0,c>0时,
则:
==1+1+3;②当a,b,c有一个为正数,另两个为负数时,设a>0,b<0,c<0,
则:
==1+(﹣1)+(﹣1)=﹣1
所以的值为3或﹣1.
【探究】请根据上面的解题思路解答下面的问题:
(1)三个有理数a,b,c满足abc<0,求的值;
(2)已知|a|=3,|b|=1,且a<b,求a+b的值.
【分析】(1)分2种情况讨论:①当a,b,c都是负数,即a<0,b<0,c<0时;②a,b,c有一个为负数,另两个为正数时,设a<0,b>0,c>0,分别求解即可;
(2)利用绝对值的代数意义,以及a小于b求出a与b的值,即可确定出a+b的值.
【解答】解:(1)∵abc<0,
∴a,b,c都是负数或其中一个为负数,另两个为正数,
①当a,b,c都是负数,即a<0,b<0,c<0时,
则=﹣﹣﹣=﹣1﹣1﹣1=﹣3;
②a,b,c有一个为负数,另两个为正数时,设a<0,b>0,c>0,
则=﹣++=﹣1+1+1=1.
(2)∵|a|=3,|b|=1,且a<b,
∴a=﹣3,b=1或﹣1,
则a+b=﹣2或﹣4.
【点评】本题主要考查了有理数的混合运算,绝对值,有理数的除法,解(1)题的关键是讨论a与ab的取值情况.
一.选择题(共12小题)
1.﹣0.25的倒数是( )
A.
B.4
C.﹣4
D.﹣5
2.-|﹣|的倒数是( )
A.
B.﹣
C.2
D.﹣2
3.a与互为相反数,则a的倒数是( )
A.
B.
C.3
D.﹣3
4.如图,数轴的单位长度为1,如果P,Q表示的数互为相反数,那么图中的4个点中,哪一个点表示的数的平方值最大( )
A.P
B.R
C.Q
D.T
5.下列说法正确的是( )
A.绝对值是本身的数是正数
B.倒数是本身的数是±1
C.平方是它本身的数是0
D.立方等于本身的数是±1
定义运算a b=a(1﹣b),下面给出的四个结论中正确的是( )
A.2 (﹣2)=﹣4
B.a b=b a
C.(﹣2) 2=2
D.若a b=0,则a=0
7.下列说法不正确的是( )
A.一个数(不为0)与它的倒数之积是1
B.一个数与它的相反数之和为0
C.两个数的商为﹣1,这两个数互为相反数
D.两个数的积为1,这两个数互为相反数
8.已知x<0,y>0,且|x|>|y|,则x+y的值是( )
A.非负数
B.负数
C.正数
D.0
9.在进行异号的两个有理数加法运算时,用到下面的一些操作:
①将绝对值较大的有理数的符号作为结果的符号并记住
②将记住的符号和绝对值的差一起作为最终的计算结果
③用较大的绝对值减去较小的绝对值
④求两个有理数的绝对值
⑤比较两个绝对值的大小
其中操作顺序正确的步骤是( )
A.①②③④⑤
B.④⑤③②①
C.①⑤③④②
D.④⑤①③②
10.古希腊数学家帕普斯是丢潘图是最得意的一个学生,有一天他向老师请教一个问题:有4个数,把其中每3个相加,其和分别是22,24,27,20,则这个四个数是( )
A.3,8,9,10
B.10,7,3,12
C.9,7,4,11
D.9,6,5,11
11.如果|a+2|和(b﹣1)2互为相反数,那么(a+b)2015的值是( )
A.﹣2015
B.2015
C.﹣1
D.1
12.如图是一个数值运算的程序,若输出的y值为3,则输入的x值为( )
A.3.5
B.﹣3.5
C.7
D.﹣7
二.填空题(共6小题)
13.绝对值大于2.6而小于5.3的所有负整数之和为______.
14.把(+5)﹣(﹣7)+(﹣23)﹣(+6)写成省略括号的和的形式为______.
15.已知a=255,b=344,c=433,则a,b,c的大小关系为______.
16.已知|x|=2,|y|=5,且x>y,则x+y=______.
17.若ab<0,则的值为______.
18.若“!”是一种数学运算符号,并且:1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则=______.
三.解答题(共9小题)
19.计算题:
(1)(﹣12)×(﹣)
(2)
﹣2.
(3)(﹣0.75)×(﹣)÷(﹣)
(4)×(2﹣5)+(﹣6)÷(﹣4)
(5)
[2﹣(﹣0.2)×(﹣)].
(6)﹣13+(﹣12)+3×[﹣(﹣1)6]﹣0.12.
(7)1﹣2+3﹣4+5﹣6+…+2007﹣2008+2009﹣2010+2011.
20.
请你参考黑板中老师的讲解,用运算律简便计算:
(1)999×(﹣15)
(2)999×118+999×(﹣)﹣999×18.
21.阅读材料,求值:1+2+22+23+24+…+22015.
解:设S=1+2+22+23+24+…+22015,将等式两边同时乘以2得:
2S=2+22+23+24+…+22015+22016
将下式减去上式得2S﹣S=22016﹣1
即S=1+2+22+23+24+…+22015=22016﹣1
请你仿照此法计算:
(1)1+2+22+23+…+210
(2)1+3+32+33+34+…+3n(其中n为正整数)
22.观察下列各等式,并回答问题:
=1﹣;
=﹣;
=﹣;
=﹣;…
(1)填空:
=______(n是正整数)
(2)计算:
++++…+=______.
(3)计算:
++++…+=______.
(4)求++++…+的值.
23.在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的“探究”
【提出问题】三个有理数a、b、c满足abc>0,求的值.
【解决问题】
解:由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c都是正数,即a>0,b>0,c>0时,
则:
==1+1+3;②当a,b,c有一个为正数,另两个为负数时,设a>0,b<0,c<0,
则:
==1+(﹣1)+(﹣1)=﹣1
所以的值为3或﹣1.
【探究】请根据上面的解题思路解答下面的问题:
(1)三个有理数a,b,c满足abc<0,求的值;
(2)已知|a|=3,|b|=1,且a<b,求a+b的值.
2016年09月23日1526467859的初中数学组卷
参考答案与试题解析
一.选择题(共12小题)
1.(2016 陕西校级三模)﹣0.25的倒数是( )
A.
B.4
C.﹣4
D.﹣5
【分析】根据倒数的定义回答即可.
【解答】解:∵﹣0.25×(﹣4)=1,
∴﹣0.25的倒数是﹣4.
故选;C.
【点评】本题主要考查的是倒数的定义,掌握倒数的定义是解题的关键.
2.(2015 攀枝花模拟)|﹣|的倒数是( )
A.
B.﹣
C.2
D.﹣2
【分析】首先根据绝对值的求法,求出|﹣|的大小;然后根据求一个数的倒数的方法,求出|﹣|的倒数是多少即可.
【解答】解:∵|﹣|=,1÷,
∴,
∴|﹣|的倒数是2.
故选:C.
【点评】(1)此题主要考查了倒数的含义和求法,要熟练掌握,解答此题的关键是要明确:乘积是1的两个数互为倒数.
(2)此题还考查了绝对值的非负性质和求法,要熟练掌握.
3.(2016 威海二模)a与互为相反数,则a的倒数是( )
A.
B.
C.3
D.﹣3
【分析】依据相反数的定义求得a的值,然后再依据倒数的定义求解即可.
【解答】解:∵﹣与互为相反数,
∴a=﹣.
∵﹣的倒数是﹣3,
∴a的倒数是﹣3.
故选:D.
【点评】本题主要考查的是相反数、倒数的定义,掌握相关定义是解题的关键.
4.(2015 杭州模拟)如图,数轴的单位长度为1,如果P,Q表示的数互为相反数,那么图中的4个点中,哪一个点表示的数的平方值最大( )
A.P
B.R
C.Q
D.T
【分析】由于点P,Q表示的数是互为相反数,根据相反数的定义易得点P表示的数为﹣2.5,Q点表示的数为2.5,则点R表示的数为﹣0.5,T点表示的数为3.5,然后求出各数的平方即可确定正确答案
【解答】解:∵点P,Q表示的数是互为相反数,
而PQ=5,
∴点P表示的数为﹣2.5,B点表示的数为2.5,
∴点R表示的数为﹣0.5,T点表示的数为3.5,
∵2.52=6.25,(﹣2.5)2=6.25,(﹣0.5)2=0.25,3.52=12.25,
∴表示的数的平方值最大的点是T.
故选D.
【点评】本题考查了数轴:数轴的三要素(原点、单位长度和正方向);数轴上左边的点表示的数比右边点表示的数大,也考查了平方与相反数,用几何方法借助数轴来求解,非常直观,且不容易遗漏,体现了数形结合的优点.
5.(2015秋 邵阳校级期末)下列说法正确的是( )
A.绝对值是本身的数是正数
B.倒数是本身的数是±1
C.平方是它本身的数是0
D.立方等于本身的数是±1
【分析】根据绝对值的性质、倒数的定义、有理数的乘方法则判断即可.
【解答】解:A、绝对值是本身的数是正数和0,故A错误;
B、倒数是本身的数是±1,故B正确;
C、平方是它本身的数是0和1,故C错误;
D、立方等于本身的数是±1和0,故D错误.
故选:B.
【点评】本题主要考查的是绝对值的性质、倒数的定义、有理数的乘方,利用0,1,﹣1的特殊性进行判断是解题的关键.
6.(2015 新市区二模)定义运算a b=a(1﹣b),下面给出的关于这种运算的四个结论中正确的是( )
A.2 (﹣2)=﹣4
B.a b=b a
C.(﹣2) 2=2
D.若a b=0,则a=0
【分析】A:根据新运算a b=a(1﹣b),求出2 (﹣2)的值是多少,即可判断出2 (﹣2)=﹣4是否正确.
B:根据新运算a b=a(1﹣b),求出a b、b a的值各是多少,即可判断出a b=b a是否正确.
C:根据新运算a b=a(1﹣b),求出(﹣2) 2的值是多少,即可判断出(﹣2) 2=2是否正确.
D:根据a b=0,可得a(1﹣b)=0,所以a=0或b=1,据此判断即可.
【解答】解:∵2 (﹣2)=2×[1﹣(﹣2)]=2×3=6,
∴选项A不正确;
∵a b=a(1﹣b),b a=b(1﹣a),
∴a b=b a只有在a=b时成立,
∴选项B不正确;
∵(﹣2) 2=(﹣2)×(1﹣2)=(﹣2)×(﹣1)=2,
∴选项C正确;
∵a b=0,
∴a(1﹣b)=0,
∴a=0或b=1
∴选项D不正确.
故选:C.
【点评】(1)此题主要考查了有理数的混合运算,要熟练掌握,解答此题的关键是要明确:①有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.②进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
(2)此题还考查了对新运算“ ”的理解和掌握,解答此题的关键是要明确:a b=a(1﹣b).
7.(2015秋 重庆期末)下列说法不正确的是( )
A.一个数(不为0)与它的倒数之积是1
B.一个数与它的相反数之和为0
C.两个数的商为﹣1,这两个数互为相反数
D.两个数的积为1,这两个数互为相反数
【分析】根据倒数、相反数、有理数的乘法和除法法则判断即可.
【解答】解:A、根据倒数的定义可知A正确,与要求不符;
B、互为相反数的两数之和为0,故B正确,与要求不符;
C、根据有理数的除法法则可知C正确,与要求不符;
D、两个数的积为1则两数互为倒数,故D错误,与要求相符.
故选:D.
【点评】本题主要考查的是倒数、相反数的定义,掌握相关法则是解题的关键.
8.(2015秋 邵阳校级期末)已知x<0,y>0,且|x|>|y|,则x+y的值是( )
A.非负数
B.负数
C.正数
D.0
【分析】绝对值不相等的异号两数相加取绝对值较大的加数的符号.
【解答】解:∵|x|>|y|,
∴x+y的符号与x的符号一致.
∵x<0,
∴x+y<0.
故选:B.
【点评】本题主要考查的是有理数的加法,判断出和的符号与x的符号一致是解题的关键.
9.(2015秋 丰台区期末)在进行异号的两个有理数加法运算时,用到下面的一些操作:
①将绝对值较大的有理数的符号作为结果的符号并记住
②将记住的符号和绝对值的差一起作为最终的计算结果
③用较大的绝对值减去较小的绝对值
④求两个有理数的绝对值
⑤比较两个绝对值的大小
其中操作顺序正确的步骤是( )
A.①②③④⑤
B.④⑤③②①
C.①⑤③④②
D.④⑤①③②
【分析】依据有理数的加法法则进行判断即可.
【解答】解;在进行异号的两个有理数加法运算时,应先求两个有理数的绝对值,然后比较两个绝对值的大小,接下来将绝对值较大的有理数的符号作为结果的符号并记住,然后用较大的绝对值减去较小的绝对值,最后将记住的符号和绝对值的差一起作为最终的计算结果,故正确的顺序是④⑤①③②.
故选:D.
【点评】本题主要考查的是有理数的加法,掌握有理数的加法法则是解题的关键.
10.(2015秋 牡丹区期末)古希腊数学家帕普斯是丢潘图是最得意的一个学生,有一天他向老师请教一个问题:有4个数,把其中每3个相加,其和分别是22,24,27,20,则这个四个数是( )
A.3,8,9,10
B.10,7,3,12
C.9,7,4,11
D.9,6,5,11
【分析】设出4个数,按照题意列出方程组,即可得出结论.
【解答】解:设a、b、c、d为这4个数,且a>b>c>d,
则有,
解得:a=11,b=9,c=7,d=4.
故选C.
【点评】本题考查的有理数的加法,解题的关键是按大小顺序设出4个数,联立方程组得出结论.
11.(2015秋 宜宾期末)如果|a+2|和(b﹣1)2互为相反数,那么(a+b)2015的值是( )
A.﹣2015
B.2015
C.﹣1
D.1
【分析】根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.
【解答】解:由题意得,|a+2|+(b﹣1)2,=0,
则|a+2|=0,(b﹣1)2=0,
解得,a=﹣2,b=1,
∴(a+b)2015=﹣1,
故选:C.
【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.
12.(2015秋 南京期末)如图是一个数值运算的程序,若输出的y值为3,则输入的x值为( )
A.3.5
B.﹣3.5
C.7
D.﹣7
【分析】由题意可得[(﹣x)﹣1]÷2=y,然后令y=3即可得到输入的x的值.
【解答】解:由题意可得,
[(﹣x)﹣1]÷2=y,
当y=3时,
[(﹣x)﹣1]÷2=3,
解得,x=﹣7,
故选D.
【点评】本题考查有理数的混合运算,解题的关键是明确题意,根据题意可以列出相应的关系式.
二.选择题(共6小题)
13.(2015秋 邵阳校级期末)绝对值大于2.6而小于5.3的所有负整数之和为 ﹣12 .
【分析】先找出符合条件的数,然后再求得它们的和即可.
【解答】解:绝对值大于2.6而小于5.3的负整数有:﹣3、﹣4、﹣5.
﹣3+(﹣4)+(﹣5)=﹣12.
故答案为:﹣12.
【点评】本题主要考查的是绝对值、有理数的加法,找出符合条件的数是解题的关键.
14.(2015秋 衡阳县期末)把(+5)﹣(﹣7)+(﹣23)﹣(+6)写成省略括号的和的形式为 5+7﹣23﹣6 .
【分析】先把减法都转化成加法,然后省略括号和加号即可.
【解答】解:(+5)﹣(﹣7)+(﹣23)﹣(+6)=(+5)+(+7)+(﹣23)+(﹣6),
则写成省略括号的和的形式为:5+7﹣23﹣6.
故答案为:5+7﹣23﹣6.
【点评】本题考查的是写成省略括号的和的形式,掌握有理数减法法则,把减法都转化成加法,并写成省略括号的和的形式是解题的关键.
15.(2015春 江都区校级月考)已知a=255,b=344,c=433,则a,b,c的大小关系为 a<c<b .
【分析】根据幂运算的性质,及它们的指数相同,只需比较它们的底数的大小,底数大的就大.
【解答】解:a=255=(25)11=3211,
b=344=(34)11=8111,
c=433=(43)11=6411,
则b>c>a.
【点评】此题要熟练运用幂运算的性质把它们变成相同的指数,然后根据底数的大小比较两个数的大小.
16.(2015秋 河东区校级期中)已知|x|=2,|y|=5,且x>y,则x+y= ﹣3或﹣7 .
【分析】先求得x、y的值,然后根据x>y分类计算即可.
【解答】解:∵|x|=2,|y|=5,
∴x=±2,y=±5.
∵x>y,
∴x=2,y=﹣5或x=﹣2,y=﹣5.
∴x+y=2+(﹣5)=﹣3或x+y=﹣2+(﹣5)=﹣7.
故答案为:﹣3或﹣7.
【点评】本题主要考查的是有理数的加法、绝对值的性质,分类讨论是解题的关键.
17.(2015秋 诸暨市校级期中)若ab<0,则的值为 1 .
【分析】由ab<0,可知a、b异号,然后利用有理数的乘法法则化简即可.
【解答】解:∵ab<0,
∴a、b异号.
∴=0.
∴=0+1=1.
故答案为:1.
【点评】本题主要考查的是绝对值的性质、有理数的除法,根据题意得出a、b异号是解题的关键.
18.(2015秋 桐乡市校级期中)若“!”是一种数学运算符号,并且:1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则= 2550 .
【分析】根据运算符号“!”的意义,然后列式计算即可.
【解答】解:
==51×50=2550.
故答案为:2550.
【点评】本题主要考查的是有理数的乘法和除法,利用定义运算是解题的关键.
三.选择题(共9小题)
19.(2015秋 房山区期末)计算:.
【分析】依据乘法的分配律计算即可.
【解答】解:原式=﹣36×﹣36×+36×
=﹣24﹣27+3
=﹣48.
【点评】本题主要考查的是有理数的乘法,依据乘法的分配律进行简便计算是解题的关键.
20.(2015秋 大石桥市期末)计算:
(1)(﹣12)×(﹣)
(2)﹣2.
【分析】(1)根据乘法的分配律进行计算即可;
(2)根据幂的乘方、绝对值、有理数的乘除和加减进行计算即可.
【解答】解:(1)(﹣12)×(﹣)
=(﹣12)×+(﹣12)×
=9+7﹣10
=6;
(2)﹣2
=﹣4+3+24×
=﹣4+3﹣
=﹣.
【点评】本题考查有理数的混合运算,解题的关键是明确乘法的分配律和有理数的混合运算的方法.
21.(2015秋 淮安校级期末)计算下列各题:
(1)﹣3﹣4+19﹣11
(2)(﹣0.75)×(﹣)÷(﹣)
(3)
[2﹣(﹣0.2)×(﹣)].
【分析】(1)根据有理数的加法和减法进行计算即可;
(2)根据有理数的乘法和加法进行计算即可;
(3)根据有理数混合运算的方法进行计算即可.
【解答】解:(1)﹣3﹣4+19﹣11
=﹣3﹣4﹣11+19
=1;
(2)(﹣0.75)×(﹣)÷(﹣)
=﹣××
=﹣;
(3)
[2﹣(﹣0.2)×(﹣)]
=
=
=
=.
【点评】本题考查有理数的混合运算,解题的关键是明确有理数混合运算的方法.
22.(2015秋 海口期末)计算:
(1)×(2﹣5)+(﹣6)÷(﹣4)
(2)(﹣+﹣)×(﹣48)
(3)﹣13+(﹣12)+3×[﹣(﹣1)6]﹣0.12.
【分析】(1)根据有理数的乘法、除法和加法进行计算即可;
(2)根据乘法的分配律进行计算即可;
(3)根据幂的乘方、有理数的乘法、加法和减法进行计算即可.
【解答】解:(1)×(2﹣5)+(﹣6)÷(﹣4)
=
=﹣2+
=﹣;
(2)(﹣+﹣)×(﹣48)
=
=8﹣36+12
=﹣16;
(3)﹣13+(﹣12)+3×[﹣(﹣1)6]﹣0.12
=﹣1+(﹣12)+3×
=﹣1+(﹣12)+3×
=﹣1+(﹣12)﹣1.5﹣0.01
=﹣14.51.
【点评】本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.
23.(2015秋 东港市期末)计算
(1)﹣10﹣8÷(﹣2)×(﹣)
(2)﹣22+(﹣3)2÷(﹣)+|﹣4|×(﹣1)2015.
【分析】(1)根据有理数的乘除法和减法进行计算即可;
(2)根据有理数的加减乘除进行计算即可.
【解答】解:(1)﹣10﹣8÷(﹣2)×(﹣)
=﹣10﹣8×
=﹣10﹣2
=﹣12;
(2)﹣22+(﹣3)2÷(﹣)+|﹣4|×(﹣1)2015
=﹣4+9×+4×(﹣1)
=﹣4﹣2﹣4
=﹣10.
【点评】本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.
24.(2016春 启东市月考)计算:1﹣2+3﹣4+5﹣6+…+2007﹣2008+2009﹣2010+2011.
【分析】根据算式的特征,应用加法结合律,分别求出﹣2+3、﹣4+5、﹣6+7、…、﹣2006+2007、﹣2008+2009、﹣2010+2011的值各是多少,进而求出算式1﹣2+3﹣4+5﹣6+…+2007﹣2008+2009﹣2010+2011的值是多少即可.
【解答】解:1﹣2+3﹣4+5﹣6+…+2007﹣2008+2009﹣2010+2011
=1+(﹣2+3)+(﹣4+5)+(﹣6+7)+…+(﹣2006+2007)+(﹣2008+2009)+(﹣2010+2011)
=1+
=1+1005
=1006
【点评】此题主要考查了有理数的加减混合运算,要熟练掌握,解答此题的关键是应用加法结合律,分别求出﹣2+3、﹣4+5、﹣6+7、…、﹣2006+2007、﹣2008+2009、﹣2010+2011的值各是多少.
25.(2016 河北)
请你参考黑板中老师的讲解,用运算律简便计算:
(1)999×(﹣15)
(2)999×118+999×(﹣)﹣999×18.
【分析】(1)将式子变形为(1000﹣1)×(﹣15),再根据乘法分配律计算即可求解;
(2)根据乘法分配律计算即可求解.
【解答】解:(1)999×(﹣15)
=(1000﹣1)×(﹣15)
=1000×(﹣15)+15
=﹣15000+15
=﹣14985;
(2)999×118+999×(﹣)﹣999×18
=999×(118﹣﹣18)
=999×100
=99900
【点评】考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.(2)进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
26.(2015秋 淮阴区期末)阅读材料,求值:1+2+22+23+24+…+22015.
解:设S=1+2+22+23+24+…+22015,将等式两边同时乘以2得:
2S=2+22+23+24+…+22015+22016
将下式减去上式得2S﹣S=22016﹣1
即S=1+2+22+23+24+…+22015=22016﹣1
请你仿照此法计算:
(1)1+2+22+23+…+210
(2)1+3+32+33+34+…+3n(其中n为正整数)
【分析】(1)根据题目中材料可以得到用类比的方法得到1+2+22+23+…+210的值;
(2)根据题目中材料可以得到用类比的方法得到1+3+32+33+34+…+3n的值.
【解答】解:(1)设S=1+2+22+23+24+…+210,
将等式两边同时乘以2,得
2S=2+22+23+24+…+211
将下式减去上式,得
2S﹣S=211﹣1
即S=1+2+22+23+24+…+210=211﹣1;
(2)设S=1+3+32+33+34+…+3n,
将等式两边同时乘以3,得
3S=3+32+33+34+…+3n+1,
将下式减去上式,得
3S﹣S=3n+1﹣1
即2S=3n+1﹣1
得S=1+3+32+33+34+…+3n=.
【点评】本题考查有理数的乘方,解题的关键是明确题意,运用题目中的解题方法,运用类比的数学思想解答问题.
四.解答题(共2小题)
27.(2015秋 重庆校级期中)观察下列各等式,并回答问题:
=1﹣;
=﹣;
=﹣;
=﹣;…
(1)填空:
= ﹣ (n是正整数)
(2)计算:
++++…+= .
(3)计算:
++++…+= .
(4)求++++…+的值.
【分析】(1)根据题意确定出拆项规律,写出第n个式子即可;
(2)根据拆项规律,先拆项再抵消写即可求解;
(3)根据拆项规律,先拆项再抵消写即可求解;
(4)根据拆项规律,先拆项再抵消写即可求解.
【解答】解:(1)=﹣(n是正整数)
(2)++++…+
=1﹣+﹣+…+﹣
=1﹣
=.
(3)++++…+
=1﹣+﹣+…+﹣
=1﹣
=.
(4)++++…+
=×(1﹣+﹣+﹣+…+﹣)
=×(1﹣)
=×
=.
故答案为:(1)﹣;
(2);(3).
【点评】考查了有理数的混合运算,(4)的关键是将式子变形为×(1﹣+﹣+﹣+…+﹣)进行计算.
28.(2015秋 烟台期中)在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的“探究”
【提出问题】三个有理数a、b、c满足abc>0,求的值.
【解决问题】
解:由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c都是正数,即a>0,b>0,c>0时,
则:
==1+1+3;②当a,b,c有一个为正数,另两个为负数时,设a>0,b<0,c<0,
则:
==1+(﹣1)+(﹣1)=﹣1
所以的值为3或﹣1.
【探究】请根据上面的解题思路解答下面的问题:
(1)三个有理数a,b,c满足abc<0,求的值;
(2)已知|a|=3,|b|=1,且a<b,求a+b的值.
【分析】(1)分2种情况讨论:①当a,b,c都是负数,即a<0,b<0,c<0时;②a,b,c有一个为负数,另两个为正数时,设a<0,b>0,c>0,分别求解即可;
(2)利用绝对值的代数意义,以及a小于b求出a与b的值,即可确定出a+b的值.
【解答】解:(1)∵abc<0,
∴a,b,c都是负数或其中一个为负数,另两个为正数,
①当a,b,c都是负数,即a<0,b<0,c<0时,
则=﹣﹣﹣=﹣1﹣1﹣1=﹣3;
②a,b,c有一个为负数,另两个为正数时,设a<0,b>0,c>0,
则=﹣++=﹣1+1+1=1.
(2)∵|a|=3,|b|=1,且a<b,
∴a=﹣3,b=1或﹣1,
则a+b=﹣2或﹣4.
【点评】本题主要考查了有理数的混合运算,绝对值,有理数的除法,解(1)题的关键是讨论a与ab的取值情况.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
