24.1.2垂径定理 课件
图片预览


文档简介
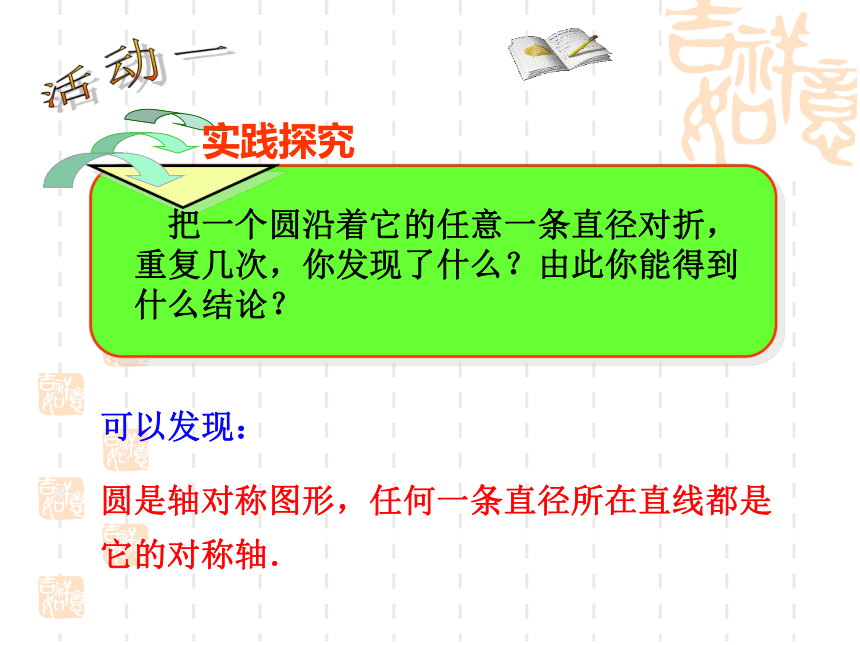
课件18张PPT。24.1.2 垂径定理 把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?可以发现:
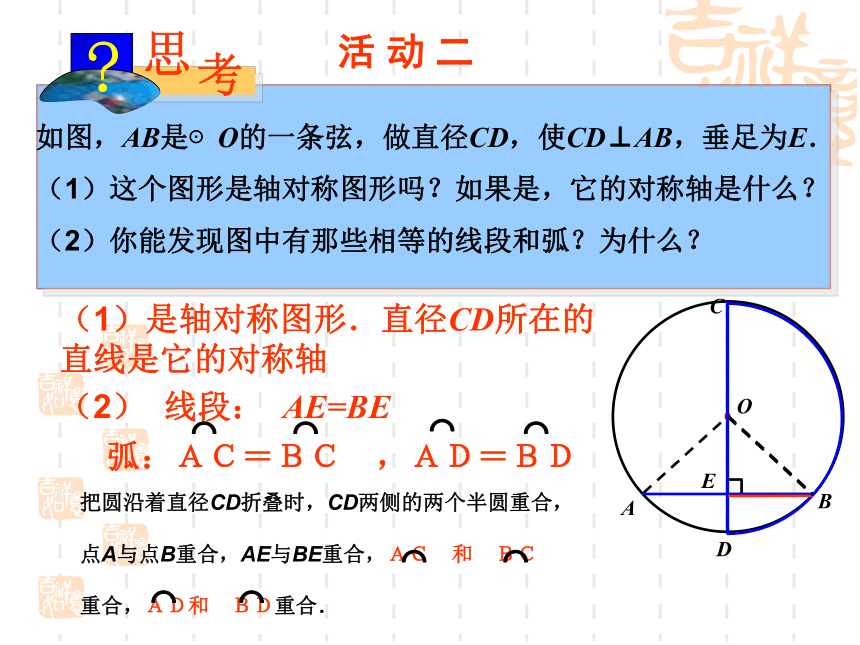
圆是轴对称图形,任何一条直径所在直线都是它的对称轴. 活动一如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
(2)你能发现图中有那些相等的线段和弧?为什么?·OABCDE活 动 二(1)是轴对称图形.直径CD所在的直线是它的对称轴(2) 线段: AE=BE把圆沿着直径CD折叠时,CD两侧的两个半圆重合,
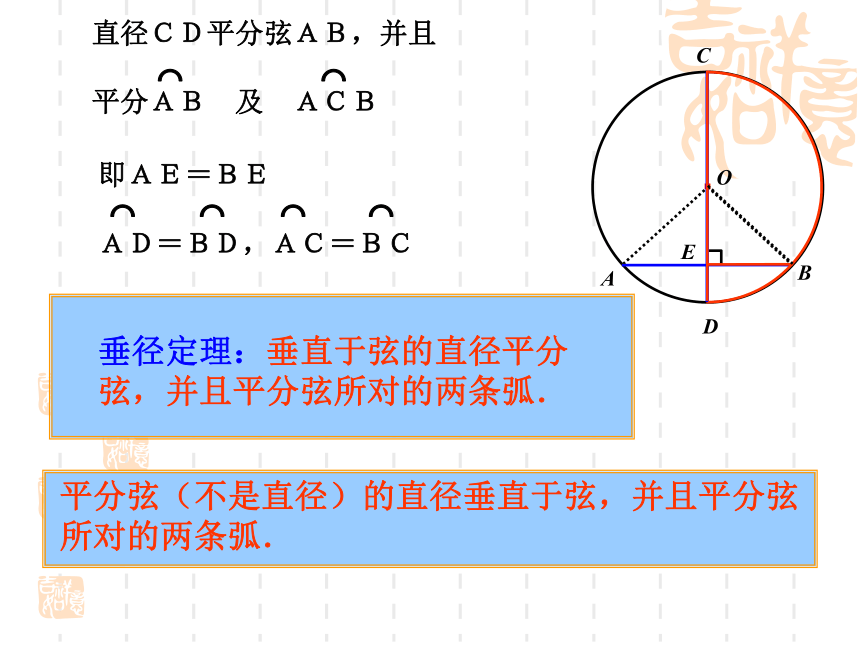
点A与点B重合,AE与BE重合,AC 和 BC
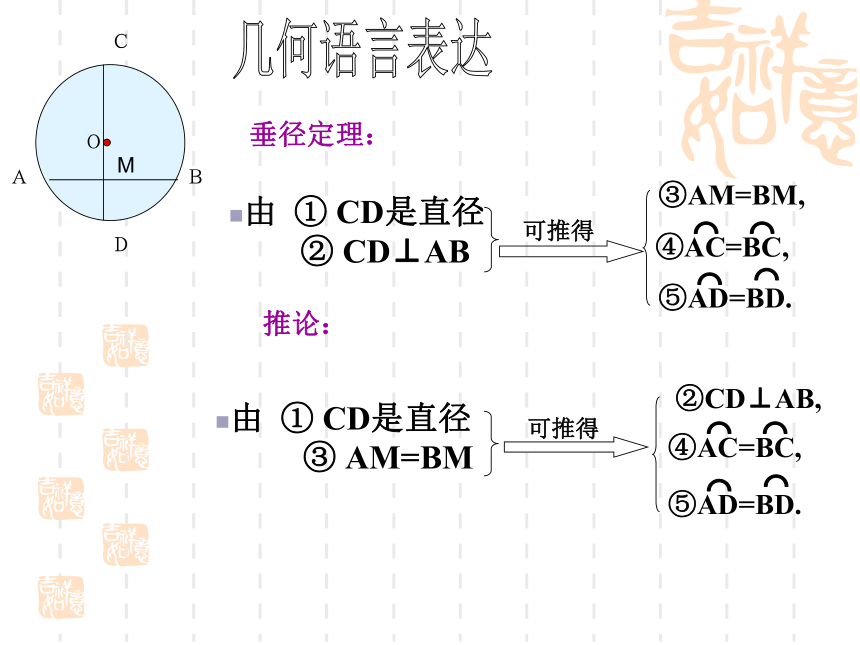
重合,AD和 BD重合.⌒⌒⌒⌒·OABCDE几何语言表达垂径定理:推论:判断下列说法的正误 ①平分弧的直径必平分弧所对的弦 ②平分弦的直线必垂直弦 ③垂直于弦的直径平分这条弦 ④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线是圆的直径 ⑥平分弦所对的一条弧的直径必垂直这条弦 ⑦在圆中,如果一条直线经过圆心且平分弦,
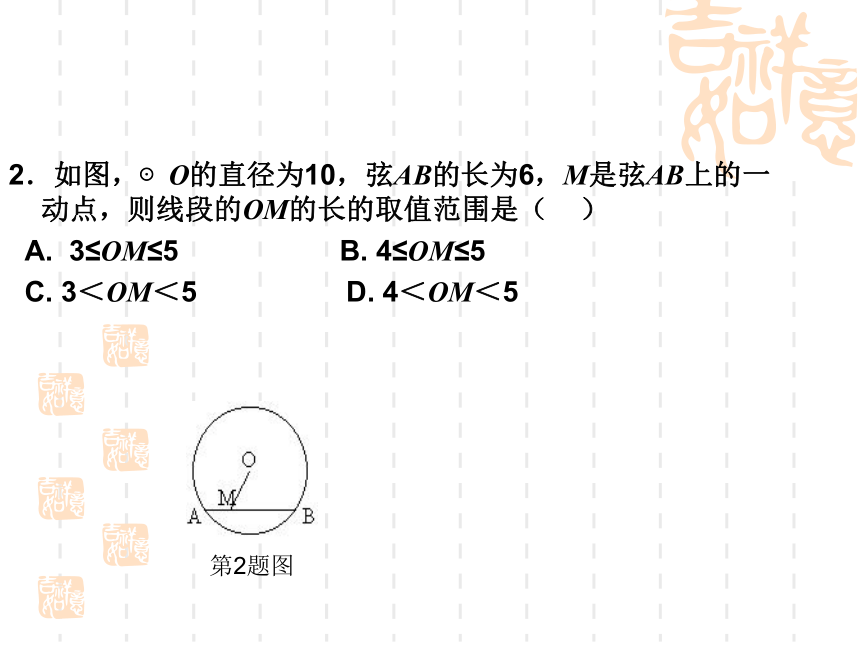
必平分此弦所对的弧 辨别是非2.如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( )
A. 3≤OM≤5 B. 4≤OM≤5
C. 3<OM<5 D. 4<OM<5第2题图问题 :你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗? 赵州桥主桥拱的半径是多少? 解得:R≈27.9(m)解决求赵州桥拱半径的问题在Rt△OAD中,由勾股定理,得即 R2=18.72+(R-7.2)2∴赵州桥的主桥拱半径约为27.9m.OA2=AD2+OD2实践应用返回退出 例题:如图 2,某居民区一处圆形水泥管下水管道破裂塌陷,
修理人员准备更换一段新管道,现量得污水面宽度为 60 cm,水
面到管道顶部距离为 10 cm,问修理人员应准备内径是多少的水
泥管道?1.如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.·OABE练习解:答:⊙O的半径为5cm.活 动 三在Rt △ AOE 中 2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.证明:∴四边形ADOE为矩形,又 ∵AC=AB∴ AE=AD∴ 四边形ADOE为正方形.挖掘潜力某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7.2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2.4m, 现有一艘宽3m,船舱顶部为长方形并高出水面(AB)2m的货船要经过拱桥,此货船能否顺利通过这座拱桥?CNMAEHFBDO返回退出探究2船能过拱桥吗如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?返回退出练习在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度. ? 650MNE 在Rt△OAD中,由勾股定理得
R2=42+(R-2.5)2
解得 R=4.45
即该圆弧形所在圆的半径为4.45米.拓展提高退出返回返回退出如图,某公司的大门呈抛物线型,大门地面宽
AB为4米,顶部C距地面的高度为4.4米。(1)在离门角A1米处垂直于地面立起一根木杆,其顶端恰好顶在抛物线型大门上的点D处,求木杆的高度。(2)一辆满载货物的汽车欲通过大门,货物顶部距地面2.65米,装货宽度为2.4米,那么这辆汽车能否顺利通过大门?返回退出小结1、要把实际问题转变成一个数学问题来解决.2、熟练地运用垂径定理及其推论、勾股定理,并用方程的思想来解决问题.3、对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量,如图有:⑴d + h = r⑵
圆是轴对称图形,任何一条直径所在直线都是它的对称轴. 活动一如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
(2)你能发现图中有那些相等的线段和弧?为什么?·OABCDE活 动 二(1)是轴对称图形.直径CD所在的直线是它的对称轴(2) 线段: AE=BE把圆沿着直径CD折叠时,CD两侧的两个半圆重合,
点A与点B重合,AE与BE重合,AC 和 BC
重合,AD和 BD重合.⌒⌒⌒⌒·OABCDE几何语言表达垂径定理:推论:判断下列说法的正误 ①平分弧的直径必平分弧所对的弦 ②平分弦的直线必垂直弦 ③垂直于弦的直径平分这条弦 ④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线是圆的直径 ⑥平分弦所对的一条弧的直径必垂直这条弦 ⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧 辨别是非2.如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( )
A. 3≤OM≤5 B. 4≤OM≤5
C. 3<OM<5 D. 4<OM<5第2题图问题 :你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗? 赵州桥主桥拱的半径是多少? 解得:R≈27.9(m)解决求赵州桥拱半径的问题在Rt△OAD中,由勾股定理,得即 R2=18.72+(R-7.2)2∴赵州桥的主桥拱半径约为27.9m.OA2=AD2+OD2实践应用返回退出 例题:如图 2,某居民区一处圆形水泥管下水管道破裂塌陷,
修理人员准备更换一段新管道,现量得污水面宽度为 60 cm,水
面到管道顶部距离为 10 cm,问修理人员应准备内径是多少的水
泥管道?1.如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.·OABE练习解:答:⊙O的半径为5cm.活 动 三在Rt △ AOE 中 2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.证明:∴四边形ADOE为矩形,又 ∵AC=AB∴ AE=AD∴ 四边形ADOE为正方形.挖掘潜力某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7.2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2.4m, 现有一艘宽3m,船舱顶部为长方形并高出水面(AB)2m的货船要经过拱桥,此货船能否顺利通过这座拱桥?CNMAEHFBDO返回退出探究2船能过拱桥吗如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?返回退出练习在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度. ? 650MNE 在Rt△OAD中,由勾股定理得
R2=42+(R-2.5)2
解得 R=4.45
即该圆弧形所在圆的半径为4.45米.拓展提高退出返回返回退出如图,某公司的大门呈抛物线型,大门地面宽
AB为4米,顶部C距地面的高度为4.4米。(1)在离门角A1米处垂直于地面立起一根木杆,其顶端恰好顶在抛物线型大门上的点D处,求木杆的高度。(2)一辆满载货物的汽车欲通过大门,货物顶部距地面2.65米,装货宽度为2.4米,那么这辆汽车能否顺利通过大门?返回退出小结1、要把实际问题转变成一个数学问题来解决.2、熟练地运用垂径定理及其推论、勾股定理,并用方程的思想来解决问题.3、对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量,如图有:⑴d + h = r⑵
同课章节目录
