【冀教版】2016版九年级上25.4.2利用两边及夹角判定两三角形相似课件
文档属性
| 名称 | 【冀教版】2016版九年级上25.4.2利用两边及夹角判定两三角形相似课件 |  | |
| 格式 | zip | ||
| 文件大小 | 374.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-23 15:27:10 | ||
图片预览




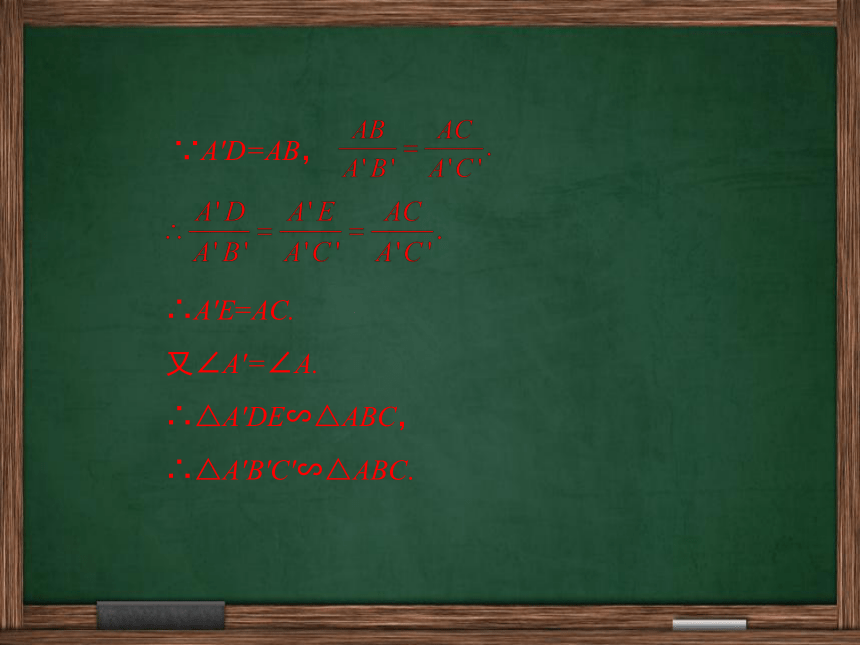
文档简介
课件11张PPT。导入新课讲授新课当堂练习课堂小结第二十五章 图形的相似25.4 相似三角形的判定第2课时 利用两边及夹角判定两三角形相似1.复习利用两角相等判定两三角形相似的方法.
2.学习利用两边及夹角判定两三角形相似的方法. (重点)
3.能够运用两边及夹角证明两个三角形相似.(难点)导入新课画一画 ①任意画△ABC;
②再画△A′B′C′,使∠A′=∠A,且
③量出B′C′及BC的长,计算 的值,并比较是否三边都对应成比例?
④量出∠B与∠B′的度数,∠B′=∠B吗?由此可推出∠C′=∠C吗?为什么?
⑤由上面的画图,你能发现△A′B′C′与△ABC有何关系?与你周围的同学交流. 我发现这两个三角形是相似的讲授新课我们来证明一下前面得出的结论:△A′B′C′∽△ABC. ∵A′D=AB,
∴A′E=AC.
又∠A′=∠A.
∴△A′DE∽△ABC,
∴△A′B′C′∽△ABC.如果一个三角形的两边长与另一个三角形的两边长对应成比例,并且夹角相等,那么这两个三角形相似 .(两边对应成比例且夹角相等,两个三角形相似)ABCA′B′C′∵A′B′:AB=A′C′:AC,∠A=∠A′ ∴△A′B′C′∽△ABC如果两个三角形两边成比例,但对应相等的角不是两条对应边的夹角,那么两个三角形是否相似呢?画一画,量一量.ABCDEF不相似探究归纳如果两个三角形两边对应成比例,但对应相等的角不是两条对应边的夹角,那么两个三角形不相似.
注意:对应相等的角一定要是两条对应边的夹角.当堂作业??1.如图,△ABC与△ADE都是等腰三角形,AD=AE,
AB=AC,∠DAB=∠CAE.求证:△ABC∽△ADE.
△ABC∽△ADE△ABC∽△DCA2.已知:如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD= ,求AD的长.课堂小结利用两边及夹角判定两三个角形相似两边对应成比例且夹角相等的两个三角形相似.
2.学习利用两边及夹角判定两三角形相似的方法. (重点)
3.能够运用两边及夹角证明两个三角形相似.(难点)导入新课画一画 ①任意画△ABC;
②再画△A′B′C′,使∠A′=∠A,且
③量出B′C′及BC的长,计算 的值,并比较是否三边都对应成比例?
④量出∠B与∠B′的度数,∠B′=∠B吗?由此可推出∠C′=∠C吗?为什么?
⑤由上面的画图,你能发现△A′B′C′与△ABC有何关系?与你周围的同学交流. 我发现这两个三角形是相似的讲授新课我们来证明一下前面得出的结论:△A′B′C′∽△ABC. ∵A′D=AB,
∴A′E=AC.
又∠A′=∠A.
∴△A′DE∽△ABC,
∴△A′B′C′∽△ABC.如果一个三角形的两边长与另一个三角形的两边长对应成比例,并且夹角相等,那么这两个三角形相似 .(两边对应成比例且夹角相等,两个三角形相似)ABCA′B′C′∵A′B′:AB=A′C′:AC,∠A=∠A′ ∴△A′B′C′∽△ABC如果两个三角形两边成比例,但对应相等的角不是两条对应边的夹角,那么两个三角形是否相似呢?画一画,量一量.ABCDEF不相似探究归纳如果两个三角形两边对应成比例,但对应相等的角不是两条对应边的夹角,那么两个三角形不相似.
注意:对应相等的角一定要是两条对应边的夹角.当堂作业??1.如图,△ABC与△ADE都是等腰三角形,AD=AE,
AB=AC,∠DAB=∠CAE.求证:△ABC∽△ADE.
△ABC∽△ADE△ABC∽△DCA2.已知:如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD= ,求AD的长.课堂小结利用两边及夹角判定两三个角形相似两边对应成比例且夹角相等的两个三角形相似.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
