【冀教版】2016版九年级上26.1.2正弦与余弦课件
文档属性
| 名称 | 【冀教版】2016版九年级上26.1.2正弦与余弦课件 |  | |
| 格式 | zip | ||
| 文件大小 | 604.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-23 15:29:07 | ||
图片预览








文档简介
课件20张PPT。导入新课讲授新课当堂练习课堂小结26.1 锐角三角函数第二十六章 解直角三角形第2课时 正弦与余弦1.理解并掌握正弦的定义,会求一个角的正弦值.(重点)
2.理解并掌握余弦的定义,会求一个角的余弦值. (重点)
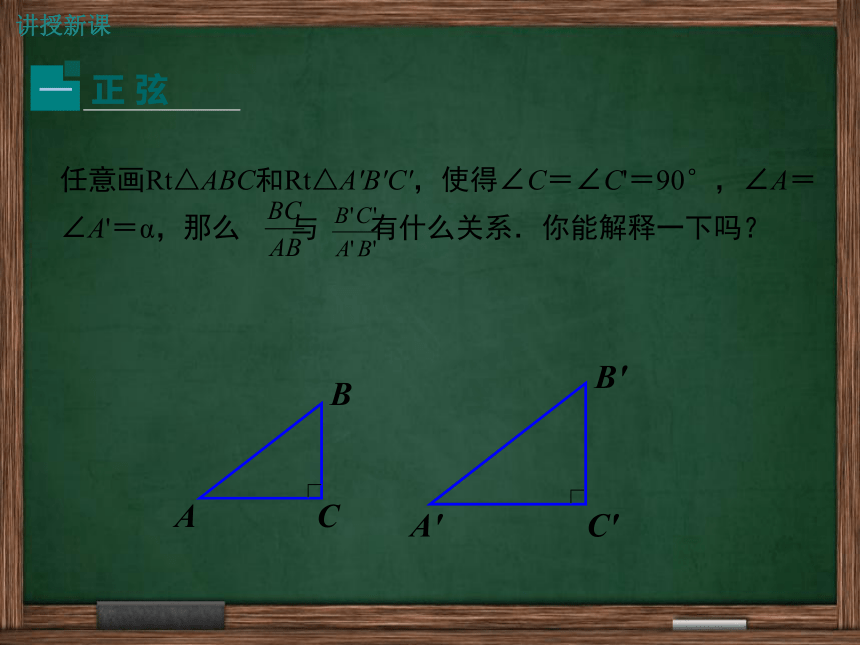
3.会推导特殊角的正弦和余弦值,并熟记这些特殊值.(难点)导入新课观察与思考为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?这个问题可以归结为,在Rt△ABC中,∠C=90°,∠A=30°,BC=35m,求AB.根据“在直角三角形中,30°角所对的边等于斜边的一半”,即可得AB=2BC=70m,也就是说,需要准备70m长的水管. 分析:讲授新课任意画Rt△ABC和Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系.你能解释一下吗? 在图中,由于∠C=∠C'=90°,∠A=∠A'=α,所以Rt△ABC∽Rt△A'B'C' 这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值. 如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sinA),记作sinA 即例如,当∠A=30°时,我们有当∠A=45°时,我们有cab对边斜边典例精析例1 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.解: (1)在Rt△ABC中,(2)在Rt△ABC中,ABCABC34135如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定,此时,其他边之间的比是否也确定了呢?为什么?任意画Rt△ABC 和Rt△A'B'C',使得∠C=∠C'=90°,∠B=∠B'=α,那么 与 有什么关系.能解释一下吗? 在图中,由于∠C=∠C'=90°,∠B=∠B'=α,所以Rt△ABC∽Rt△A'B'C'.如图:在Rt △ABC中,∠C=90°,正弦余弦1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构 造直角三角形).
2.sinA、 cosA是一个比值(数值).
3.sinA、 cosA的大小只与∠A的大小有关,而与直角三角形的边长无关.如图,观察一副三角板,它们其中有几个锐角?分别是多少度?
(1)sin30°,cos30°等于多少?300600450450(2)sin60°,cos60°等于多少?(3)sin45°,cos45°等于多少?请与同伴交流你是怎么想的?又是怎么做的?))))特殊角的正弦、余弦值:(1)sin30°= ,cos30°= . (2)sin60°= ,cos60°= . (3)sin45°= ,cos45°= .30°、45°、60°角的正弦值、余弦值和正切值如下表:1. 分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.解:由勾股定理当堂练习2. 在Rt△ABC中,如果各边长都扩大到原来的2倍,那么锐角A的正弦值、余弦值和正切值有什么变化?解:设各边长分别为a、b、c,∠A的三个三角函数分别为则扩大2倍后三边分别为2a、2b、2c∴都不变.3. 如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,求:sinA、cosB的值.ABC8解:课堂小结在Rt△ABC中锐角三角函数30°、45°、60°角的正弦值、余弦值和正切值如下表:
2.理解并掌握余弦的定义,会求一个角的余弦值. (重点)
3.会推导特殊角的正弦和余弦值,并熟记这些特殊值.(难点)导入新课观察与思考为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?这个问题可以归结为,在Rt△ABC中,∠C=90°,∠A=30°,BC=35m,求AB.根据“在直角三角形中,30°角所对的边等于斜边的一半”,即可得AB=2BC=70m,也就是说,需要准备70m长的水管. 分析:讲授新课任意画Rt△ABC和Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系.你能解释一下吗? 在图中,由于∠C=∠C'=90°,∠A=∠A'=α,所以Rt△ABC∽Rt△A'B'C' 这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值. 如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sinA),记作sinA 即例如,当∠A=30°时,我们有当∠A=45°时,我们有cab对边斜边典例精析例1 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.解: (1)在Rt△ABC中,(2)在Rt△ABC中,ABCABC34135如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定,此时,其他边之间的比是否也确定了呢?为什么?任意画Rt△ABC 和Rt△A'B'C',使得∠C=∠C'=90°,∠B=∠B'=α,那么 与 有什么关系.能解释一下吗? 在图中,由于∠C=∠C'=90°,∠B=∠B'=α,所以Rt△ABC∽Rt△A'B'C'.如图:在Rt △ABC中,∠C=90°,正弦余弦1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构 造直角三角形).
2.sinA、 cosA是一个比值(数值).
3.sinA、 cosA的大小只与∠A的大小有关,而与直角三角形的边长无关.如图,观察一副三角板,它们其中有几个锐角?分别是多少度?
(1)sin30°,cos30°等于多少?300600450450(2)sin60°,cos60°等于多少?(3)sin45°,cos45°等于多少?请与同伴交流你是怎么想的?又是怎么做的?))))特殊角的正弦、余弦值:(1)sin30°= ,cos30°= . (2)sin60°= ,cos60°= . (3)sin45°= ,cos45°= .30°、45°、60°角的正弦值、余弦值和正切值如下表:1. 分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.解:由勾股定理当堂练习2. 在Rt△ABC中,如果各边长都扩大到原来的2倍,那么锐角A的正弦值、余弦值和正切值有什么变化?解:设各边长分别为a、b、c,∠A的三个三角函数分别为则扩大2倍后三边分别为2a、2b、2c∴都不变.3. 如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,求:sinA、cosB的值.ABC8解:课堂小结在Rt△ABC中锐角三角函数30°、45°、60°角的正弦值、余弦值和正切值如下表:
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
