28.3圆内接四边形课件

课件11张PPT。导入新课讲授新课当堂练习课堂小结28.3 圆心角和圆周角第二十八章 圆第3课时 圆内接四边形1.复习并巩固圆周角和圆心角的相关知识.
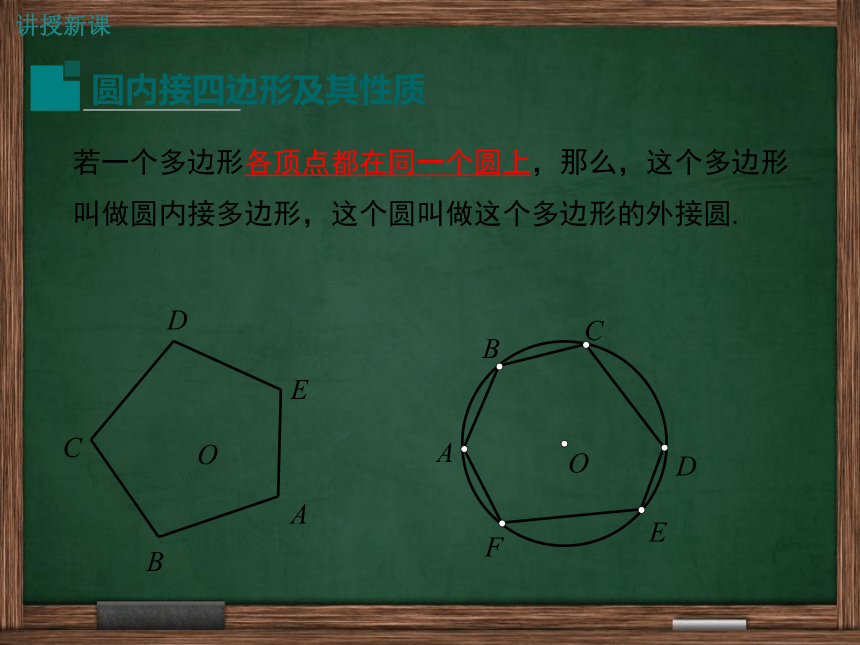
2.理解并掌握圆内接四边形的概念及性质并学会运用. (重点)问题1 什么是圆周角？ 导入新课回顾与思考特征：① 角的顶点在圆上.② 角的两边都与圆相交.圆周角概念: 顶点在圆上,并且两边都和圆相交的角叫圆周角.问题2 什么是圆周角定理？ 圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半.即 ∠ABC = ∠AOC.讲授新课若一个多边形各顶点都在同一个圆上，那么，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆.OACDEB 如图，四边形ABCD为⊙O的内接四边形；⊙O为四边形ABCD的外接圆.CODBA∵ 弧BCD和弧BAD所对的圆心角的和是周角，∴∠A＋∠C＝180°，同理∠B＋∠D＝180°，E延长BC到点E，有∠BCD＋∠DCE＝180°.∴∠A＝∠DCE.
定理：圆的内接四边形的对角互补，且任何一个外角都等于它的内对角. 由于∠A是∠DCE的补角∠BCD的对角（简称∠DCE的内对角），于是我们得到圆内接四边形的性质：当堂练习1.在⊙O中，∠CBD=30°，∠BDC=20°,求∠A.解：∵∠CBD=30°，∠BDC=20°
∴∠C=180°-∠CBD-∠BDC=130°
∴∠A=180°-∠C=50°（圆内接四边形对角互补）变式：已知∠OAB等于40°,求∠C 的度数. ABCOD2.判断.
（1）等弧所对的圆周角相等；（ ）
（2）相等的弦所对的圆周角也相等；（ ）
（3）90°的角所对的弦是直径；（ ）
（4）同弦所对的圆周角相等.（ ）××××课堂小结2.圆内接四边形的性质定理：圆的内接四边形的对角互补，且任何一个外角都等于它的内对角.1.若一个四边形各顶点都在同一个圆上，那么，这个四边形叫做圆内接四边形，这个圆叫做这个四边形的外接圆.