山东省巨野县第一中学高中数学必修一课件:3.1.2 用二分法求方程的近似解 (共18张PPT)
文档属性
| 名称 | 山东省巨野县第一中学高中数学必修一课件:3.1.2 用二分法求方程的近似解 (共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 305.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-24 00:00:00 | ||
图片预览






文档简介
课件18张PPT。3.1.2 用二分法
求方程的近似解复习旧知什么叫函数的零点?零点的等价性含义是什么?零点存在性定理是什么?问题:你会解下列方程吗?
2x-6=0; 2x2-3x+1=0; lnx+2x-6=0 求方程根的问题
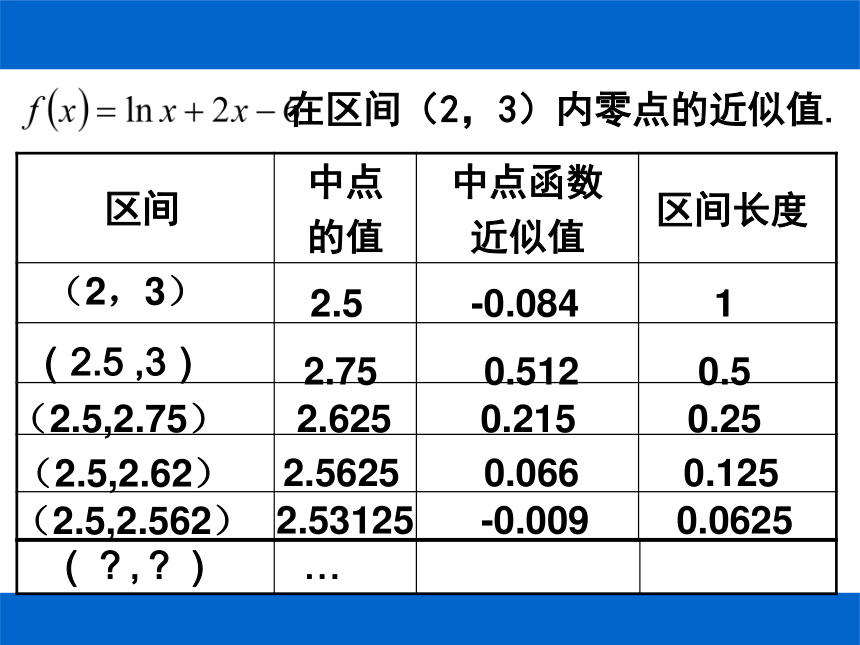
相应函数的零点问题你会求方程lnx+2x-6=0的近似解吗?思路如何找到零点近似值 ??问可以转化为函数 在区间(2,3)内零点的近似值。
求方程 的近似解的问题问题 在区间(2,3)内零点的近似值.(2.5,2.75)(2.5,2.562)2.52.752.6252.5625(2.5,2.62)-0.0840.5120.2150.06610.50.250.1250.0625(2.5 ,3)区间长度区间2.53125-0.009(?,?)…思考:
通过这种方法,是否可以得到任意精确度的近似值? (如精确度为0.01) 精确度为0.01,即零点值与近似值的差的绝对值要小于或等于0.01结论1.通过这样的方法,我们可以得到任意精确度的零点近似值.2.给定一个精确度,即要求误差不超过某个数如0.01时,可以通过有限次不断地重复上述缩小零点所在区间的方法步骤,而使最终所得的零点所在的小区间内的任意一点,与零点的误差都不超过给定的精确度,即都可以作为零点的近似值.3.本题中,如在精确度为0.01的要求下,我们可以将区间(2.53125,2.5390625)内的任意点及端点作为此函数在区间(2,3)内的零点近似值.4.若再将近似值保留两为小数,那么2.53,2.54都可以作为在精确度为0.01的要求下的函数在(2,3)内的零点的近似值.一般地,为便于计算机操作,常取区间端点作为零点的近似值,即2.53125(2,3)(2.5,3)(2.5,2.75)(2.5,2.5625)(2.53125,2.5625)(2.53125,2.546875)(2.53125,2.5390625)2.52.752.6252.56252.531252.546875(2.5,2.625)2.53906252.53515625-0.0840.5120.2150.066-0.0090.0290.0100.00110.50.250.1250.06250.031250.0156250.0078125(精确度为0.01) 所以我们可将此区间内的任意一点作为函数零点的近似值,特别地,可以将区间端点作为零点的近似值.由于如图所以方程的近似解为 对于在区间 上连续不断且 的函
数 ,通过不断地把函数 的零点所在的区
间一分为二,使区间的两个端点逐步逼近零点,进而得到
零点近似值的方法叫做二分法.二分法概念问题5: 你能归纳出“给定精确度ε,用二分法求函数零点近似值的步骤”吗?二分法的实质:就是将函数零点所在的区间不断地一分为二,使新得到的区间不断变小,两个端点逐步逼近零点.3.计算 ;(1)若 ,则 就是函数的零点; 1.确定区间 ,验证 ,给定精确度 ; 2.求区间 的中点 ; (2)若 ,则令 (此时零点 ). (3)若 ,则令 (此时零点 ). 4.判断是否达到精确度 :即若 ,则得到零点
近似值 (或 );否则重复2~4. 给定精确度 ,用二分法求函数 零点近似值的步骤如下:012346578-6-2310214075142273列表例2:借助计算器或计算机用二分法求方程2x+3x=7的近似解(精确度0.1).先确定零点的范围;再用二分法去求方程的近似解 取(1,1.5)的中点x2=1.25 ,f(1.25)= -0.87,因为f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5) 同理可得, x0∈(1.375,1.5),x0∈(1.375,1.4375),由于 |1.375-1.4375|=0.0625< 0.1 所以,原方程的近似解可取为1.4375 转化思想逼近思想小结二分法数形结合1.寻找解所在的区间2.不断二分解所在的区间3.根据精确度得出近似解用二分法求
方程的近似解基本知识:1. 二分法的定义;
2.用 二分法求解方程的近似解的步骤. 通过本节课的学习,你学会了
哪些知识? 定区间,找中点,中值计算两边看;同号去,异号算,零点落在异号间;周而复始怎么办?精确度上来判断.二分法求方程近似解的口诀:练习借助计算器用二分法求
的近似解(精确度0.1).方程的近似解为
相应函数的零点问题你会求方程lnx+2x-6=0的近似解吗?思路如何找到零点近似值 ??问可以转化为函数 在区间(2,3)内零点的近似值。
求方程 的近似解的问题问题 在区间(2,3)内零点的近似值.(2.5,2.75)(2.5,2.562)2.52.752.6252.5625(2.5,2.62)-0.0840.5120.2150.06610.50.250.1250.0625(2.5 ,3)区间长度区间2.53125-0.009(?,?)…思考:
通过这种方法,是否可以得到任意精确度的近似值? (如精确度为0.01) 精确度为0.01,即零点值与近似值的差的绝对值要小于或等于0.01结论1.通过这样的方法,我们可以得到任意精确度的零点近似值.2.给定一个精确度,即要求误差不超过某个数如0.01时,可以通过有限次不断地重复上述缩小零点所在区间的方法步骤,而使最终所得的零点所在的小区间内的任意一点,与零点的误差都不超过给定的精确度,即都可以作为零点的近似值.3.本题中,如在精确度为0.01的要求下,我们可以将区间(2.53125,2.5390625)内的任意点及端点作为此函数在区间(2,3)内的零点近似值.4.若再将近似值保留两为小数,那么2.53,2.54都可以作为在精确度为0.01的要求下的函数在(2,3)内的零点的近似值.一般地,为便于计算机操作,常取区间端点作为零点的近似值,即2.53125(2,3)(2.5,3)(2.5,2.75)(2.5,2.5625)(2.53125,2.5625)(2.53125,2.546875)(2.53125,2.5390625)2.52.752.6252.56252.531252.546875(2.5,2.625)2.53906252.53515625-0.0840.5120.2150.066-0.0090.0290.0100.00110.50.250.1250.06250.031250.0156250.0078125(精确度为0.01) 所以我们可将此区间内的任意一点作为函数零点的近似值,特别地,可以将区间端点作为零点的近似值.由于如图所以方程的近似解为 对于在区间 上连续不断且 的函
数 ,通过不断地把函数 的零点所在的区
间一分为二,使区间的两个端点逐步逼近零点,进而得到
零点近似值的方法叫做二分法.二分法概念问题5: 你能归纳出“给定精确度ε,用二分法求函数零点近似值的步骤”吗?二分法的实质:就是将函数零点所在的区间不断地一分为二,使新得到的区间不断变小,两个端点逐步逼近零点.3.计算 ;(1)若 ,则 就是函数的零点; 1.确定区间 ,验证 ,给定精确度 ; 2.求区间 的中点 ; (2)若 ,则令 (此时零点 ). (3)若 ,则令 (此时零点 ). 4.判断是否达到精确度 :即若 ,则得到零点
近似值 (或 );否则重复2~4. 给定精确度 ,用二分法求函数 零点近似值的步骤如下:012346578-6-2310214075142273列表例2:借助计算器或计算机用二分法求方程2x+3x=7的近似解(精确度0.1).先确定零点的范围;再用二分法去求方程的近似解 取(1,1.5)的中点x2=1.25 ,f(1.25)= -0.87,因为f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5) 同理可得, x0∈(1.375,1.5),x0∈(1.375,1.4375),由于 |1.375-1.4375|=0.0625< 0.1 所以,原方程的近似解可取为1.4375 转化思想逼近思想小结二分法数形结合1.寻找解所在的区间2.不断二分解所在的区间3.根据精确度得出近似解用二分法求
方程的近似解基本知识:1. 二分法的定义;
2.用 二分法求解方程的近似解的步骤. 通过本节课的学习,你学会了
哪些知识? 定区间,找中点,中值计算两边看;同号去,异号算,零点落在异号间;周而复始怎么办?精确度上来判断.二分法求方程近似解的口诀:练习借助计算器用二分法求
的近似解(精确度0.1).方程的近似解为
