山东省巨野县第一中学高中数学人教版必修二课件:2.2.3 直线与平面平行的性质 (共21张PPT)
文档属性
| 名称 | 山东省巨野县第一中学高中数学人教版必修二课件:2.2.3 直线与平面平行的性质 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 377.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-24 00:00:00 | ||
图片预览




文档简介
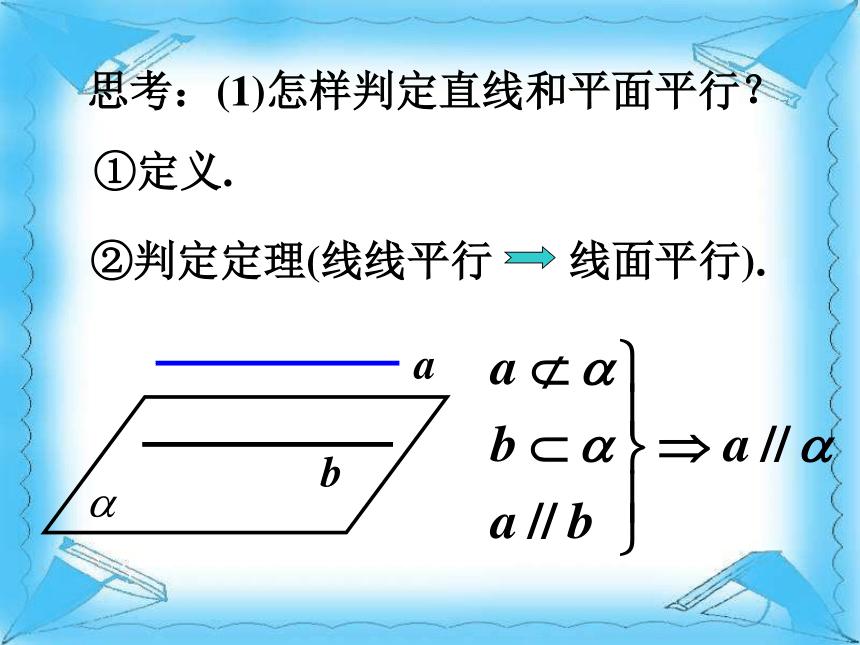
课件21张PPT。2.2.3直线与平面平行的性质思考:(1)怎样判定直线和平面平行? ①定义. ?
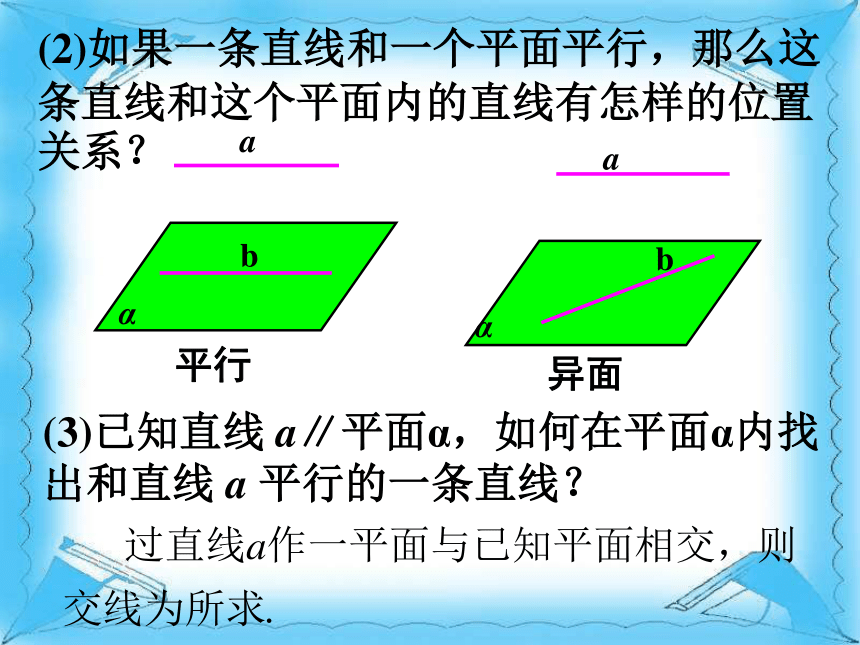
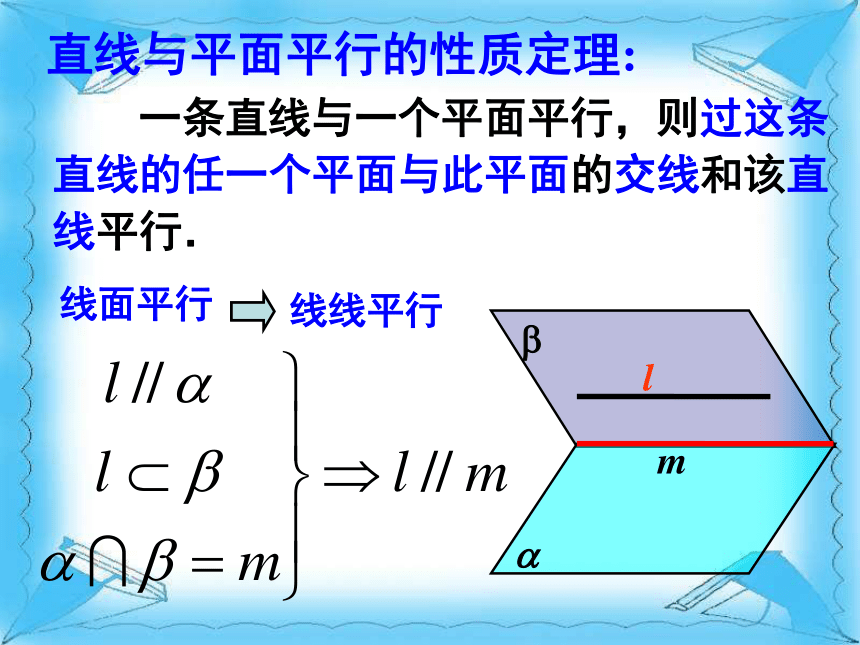
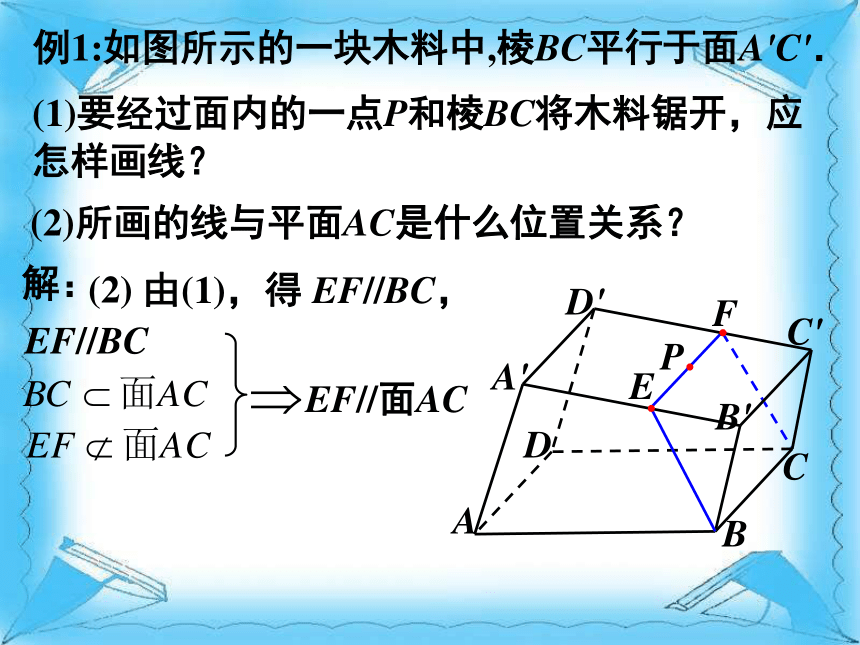
(2)如果一条直线和一个平面平行,那么这条直线和这个平面内的直线有怎样的位置关系? (3)已知直线 a∥平面α,如何在平面α内找出和直线 a 平行的一条直线? 平行异面?ml?直线与平面平行的性质定理: 一条直线与一个平面平行,则过这条直线的任一个平面与此平面的交线和该直线平行.线面平行线线平行(2) 例1:如图所示的一块木料中,棱BC平行于面A'C'.解:(1)要经过面内的一点P和棱BC将木料锯开,应
怎样画线?(2)所画的线与平面AC是什么位置关系?EF//面AC由(1),得EF//BC,EF//BC( )( )( )练习:判断下列命题是否正确?(1)若直线a与平面?平行,则a与?内任何直线平行. ( )推论:平面外的两条平行直线中的一条平行于这个平面,则另一条也平行于这个平面.abc线面平行线线平行线面平行练习:在空间四边形ABCD中,E,F,G,H分别为AC,BC,BD,AD上的点,若四边形EFGH为平行四边形。
求证:AB∥平面EFGH。2.2.4平面与平面平行的性质问题:下面两组平面哪一组看上去象平行平面?(1)(2) 如果一个平面与两个平行平面相交,会有什么结果出现?αβab平面与平面平行的性质定理:面面平行线线平行两个平行平面同时和第三个平面相交,那么它们的交线平行. 两个平面没有公共点 两平面平行 内任何两条直线都没有公共点 内的任何一条直线与 都无公共点 }面面平行性质2面面平行 线面平行3、夹在两个平行平面间的平行线段相等。4、经过平面外一点只有一个平面和已知平面平行。 平面与平面平行的其他性质:已知:求证:AB=CD例1:求证:夹在两个平行平面间的两条
平行线段相等.证明:已知:求证:AB=CDBACDACBDAC//BD练习:证明:过A作直线AH//DF,连结AD,GE,HFNHEDABCPM例2:在四棱锥P-ABCD中,底面ABCD是矩形,M、N是
AB、PC上的点,且 求证:MN∥平面PAD.解:四边形AMNH是平行四边形【总一总★成竹在胸】面面平行判定定理: 如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行。推论: 如果一个平面内有两条相交直线分别平行于
另一个平面内的两条直线,那么这两个平面平行面面平行性质定理: 如果两个平行平面同时与第三个平面相交,那么它们的交线平行。再见!
(2)如果一条直线和一个平面平行,那么这条直线和这个平面内的直线有怎样的位置关系? (3)已知直线 a∥平面α,如何在平面α内找出和直线 a 平行的一条直线? 平行异面?ml?直线与平面平行的性质定理: 一条直线与一个平面平行,则过这条直线的任一个平面与此平面的交线和该直线平行.线面平行线线平行(2) 例1:如图所示的一块木料中,棱BC平行于面A'C'.解:(1)要经过面内的一点P和棱BC将木料锯开,应
怎样画线?(2)所画的线与平面AC是什么位置关系?EF//面AC由(1),得EF//BC,EF//BC( )( )( )练习:判断下列命题是否正确?(1)若直线a与平面?平行,则a与?内任何直线平行. ( )推论:平面外的两条平行直线中的一条平行于这个平面,则另一条也平行于这个平面.abc线面平行线线平行线面平行练习:在空间四边形ABCD中,E,F,G,H分别为AC,BC,BD,AD上的点,若四边形EFGH为平行四边形。
求证:AB∥平面EFGH。2.2.4平面与平面平行的性质问题:下面两组平面哪一组看上去象平行平面?(1)(2) 如果一个平面与两个平行平面相交,会有什么结果出现?αβab平面与平面平行的性质定理:面面平行线线平行两个平行平面同时和第三个平面相交,那么它们的交线平行. 两个平面没有公共点 两平面平行 内任何两条直线都没有公共点 内的任何一条直线与 都无公共点 }面面平行性质2面面平行 线面平行3、夹在两个平行平面间的平行线段相等。4、经过平面外一点只有一个平面和已知平面平行。 平面与平面平行的其他性质:已知:求证:AB=CD例1:求证:夹在两个平行平面间的两条
平行线段相等.证明:已知:求证:AB=CDBACDACBDAC//BD练习:证明:过A作直线AH//DF,连结AD,GE,HFNHEDABCPM例2:在四棱锥P-ABCD中,底面ABCD是矩形,M、N是
AB、PC上的点,且 求证:MN∥平面PAD.解:四边形AMNH是平行四边形【总一总★成竹在胸】面面平行判定定理: 如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行。推论: 如果一个平面内有两条相交直线分别平行于
另一个平面内的两条直线,那么这两个平面平行面面平行性质定理: 如果两个平行平面同时与第三个平面相交,那么它们的交线平行。再见!
