曲线的参数方程
图片预览

文档简介
曲线的参数方程
教学目标
1. 弄清曲线参数方程的概念
2. 能选取适当的参数,求简单曲线的参数方程
3、初步了解如何应用参数方程来解决某些具体问题,在问题解决的过程中,形成数学抽象思维能力,初步体验参数的基本思想。
教学重点
曲线参数方程的概念、方法
教学难点
曲线参数方程的探求。
教学过程
一、曲线的参数方程概念的引入
探究:
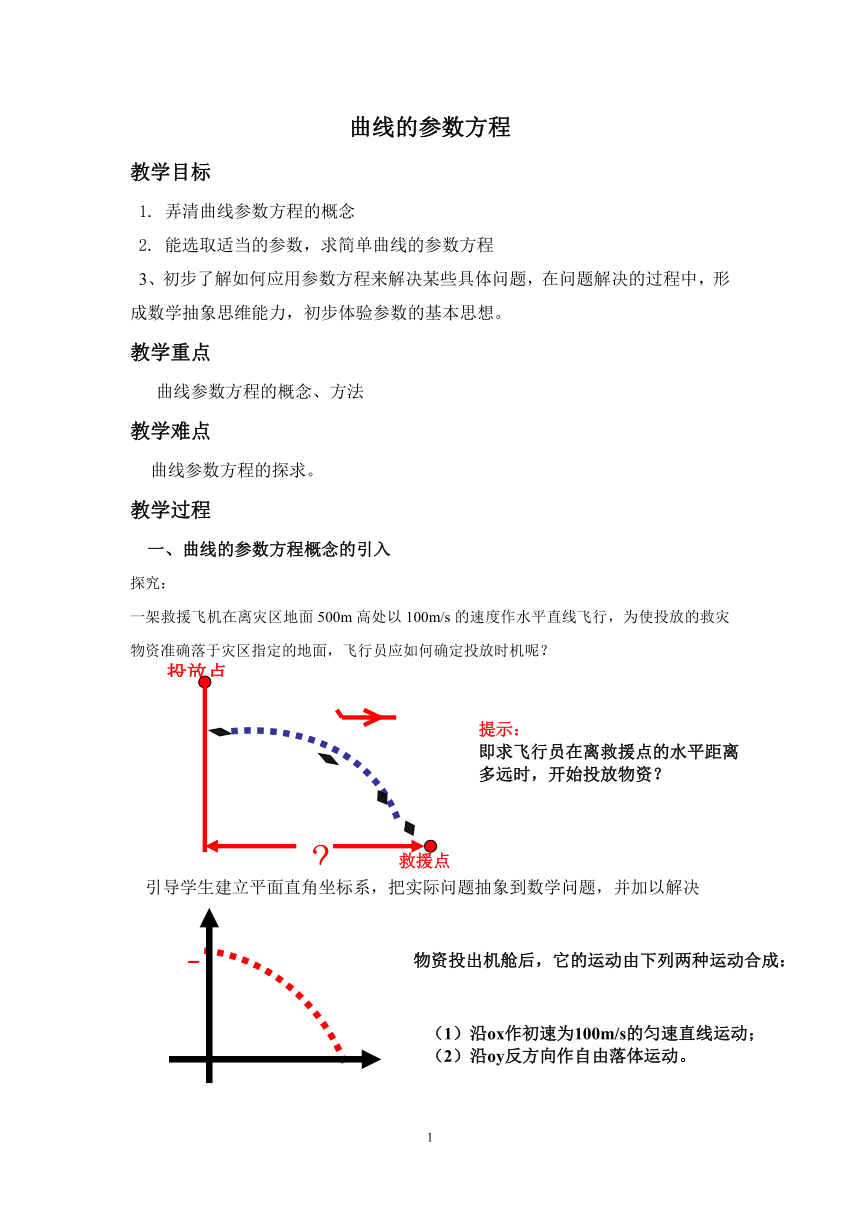
一架救援飞机在离灾区地面500m高处以100m/s的速度作水平直线飞行,为使投放的救灾物资准确落于灾区指定的地面,飞行员应如何确定投放时机呢?
引导学生建立平面直角坐标系,把实际问题抽象到数学问题,并加以解决
物质出仓后在t时刻,它在水平方向的位移量x=100t,离地面的高度y=500- gt2,即
X=100t
( G=9.8m/s2) ①
Y=500- gt2 ,
当y=0 ,即500--gt2=0,解得t= 10.10 ,代入①得x≈1010m.所以飞行员在离救援地点的水平距离约为1010m时投放物质,可以使其准确落在指定地点。
(1、通过生活中的实例,引发学生研究的兴趣;2、通过引例明确学习参数方程的现实意义;3、通过对问题的解决,使学生体会到仅仅运用一种方程来研究往往难以获得满意的结果,从而了解学习曲线的参数方程的必要性;4、通过具体的问题,让学生找到解决问题的途径,为研究圆的参数方程作准备。)
二、参数方程的概念
一般地, 在平面直角坐标系中,如果曲线上任意一点的坐标x, y都是某个变数t的函数
X=f(t)
②
Y=g(t)
并且对于t的每一个允许值, 由方程组② 所确定的点M(x,y)都在这条曲线上, 那么方程② 就叫做这条曲线的参数方程, 联系变数x,y的变数t叫做参变数, 简称参数
相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程。
关于参数几点说明: 参数是联系变数x,y的桥梁,
1. 参数方程中参数可以是有物理意义, 几何意义, 也可以没有明显意义。
2.同一曲线选取参数不同, 曲线参数方程形式也不一样
3.在实际问题中要确定参数的取值范围
三、讲解例题
X=3t
例1: 已知曲线C的参数方程是 (t为参数)
Y=2t2+1
(1)判断点M1(0, 1),M2(5, 4)与曲线C的位置关系;
(2)已知点M3(6, a)在曲线C上, 求a的值。
解:略
课堂练习:
x=1+t2
1、曲线 (t为参数)与坐标轴的交点坐标是( )
Y=4t—3
A. (1,4) B (,0) C(1,-3) D(±,0)
X=sinΦ
2方程 (Φ为参数)所表示的曲线上一点的坐标是( )
Y=COSΦ
A(2,7) B(,) C(,) D(1,0)
X=1+2t
例2、已知曲线C的参数方程是 (t为参数,a R)
Y=at2
点M(5,4)在该C 曲线上。(1)求常数a ; (2)求曲线C的普通方程。
5=1+2t a=1
解:(1)由题意得 解得 ∴ a=1
4= at2 t=2
X=1+2t
(2)由已知(1)可得,曲线C的方程
Y=t2
由第一个方程得:t= ,代入第二个方程得 y= 所以(x-1)2=4y为所求。
思考题:动点M作等速直线运动, 它在x轴和y轴方向的速度分别为5和12 , 运动开始时位于点P(1,2), 求点M的轨迹参数方程。
X=1+5t
解:设动点M (x,y) 运动时间为t,依题意,得
Y=2+2t
X=1+5t
所以,点M的轨迹参数方程为
Y=2+12t
参数方程求法:
(1)建立直角坐标系, 设曲线上任一点P坐标为x,y
(2)选取适当的参数
(3)根据已知条件和图形的几何性质, 物理意义, 建立点P坐标与参数的函数式
(4)证明这个参数方程就是所由于的曲线的方程
四、小结:
一般地,在平面直角坐标系中,如果曲线上任意一点的坐标
X=f(t)
x,y都是某个变数t的函数 (2)
y=g(t)
并且对于t的每一个允许值,由方程组(2)所确定的点M(x,y)都在这条曲线上,那么方程(2)就叫做这条曲线的参数方程, 系变数x,y的变数t叫做参变数,简称参数。
五、作业P26习题 2.1 T1,T2,T3,T4
课题:曲线的参数方程
学 科:高 中 数 学
姓 名: 严 政
单 位:固镇县新马桥中学
2010年5月
oooo
500
提示:
即求飞行员在离救援点的水平距离
多远时,开始投放物资?
投放点
救援点
?
2010年教师资格
认定教学设计
解析几何初步
y
x
物资投出机舱后,它的运动由下列两种运动合成:
(1)沿ox作初速为100m/s的匀速直线运动;
(2)沿oy反方向作自由落体运动。
PAGE
5
教学目标
1. 弄清曲线参数方程的概念
2. 能选取适当的参数,求简单曲线的参数方程
3、初步了解如何应用参数方程来解决某些具体问题,在问题解决的过程中,形成数学抽象思维能力,初步体验参数的基本思想。
教学重点
曲线参数方程的概念、方法
教学难点
曲线参数方程的探求。
教学过程
一、曲线的参数方程概念的引入
探究:
一架救援飞机在离灾区地面500m高处以100m/s的速度作水平直线飞行,为使投放的救灾物资准确落于灾区指定的地面,飞行员应如何确定投放时机呢?
引导学生建立平面直角坐标系,把实际问题抽象到数学问题,并加以解决
物质出仓后在t时刻,它在水平方向的位移量x=100t,离地面的高度y=500- gt2,即
X=100t
( G=9.8m/s2) ①
Y=500- gt2 ,
当y=0 ,即500--gt2=0,解得t= 10.10 ,代入①得x≈1010m.所以飞行员在离救援地点的水平距离约为1010m时投放物质,可以使其准确落在指定地点。
(1、通过生活中的实例,引发学生研究的兴趣;2、通过引例明确学习参数方程的现实意义;3、通过对问题的解决,使学生体会到仅仅运用一种方程来研究往往难以获得满意的结果,从而了解学习曲线的参数方程的必要性;4、通过具体的问题,让学生找到解决问题的途径,为研究圆的参数方程作准备。)
二、参数方程的概念
一般地, 在平面直角坐标系中,如果曲线上任意一点的坐标x, y都是某个变数t的函数
X=f(t)
②
Y=g(t)
并且对于t的每一个允许值, 由方程组② 所确定的点M(x,y)都在这条曲线上, 那么方程② 就叫做这条曲线的参数方程, 联系变数x,y的变数t叫做参变数, 简称参数
相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程。
关于参数几点说明: 参数是联系变数x,y的桥梁,
1. 参数方程中参数可以是有物理意义, 几何意义, 也可以没有明显意义。
2.同一曲线选取参数不同, 曲线参数方程形式也不一样
3.在实际问题中要确定参数的取值范围
三、讲解例题
X=3t
例1: 已知曲线C的参数方程是 (t为参数)
Y=2t2+1
(1)判断点M1(0, 1),M2(5, 4)与曲线C的位置关系;
(2)已知点M3(6, a)在曲线C上, 求a的值。
解:略
课堂练习:
x=1+t2
1、曲线 (t为参数)与坐标轴的交点坐标是( )
Y=4t—3
A. (1,4) B (,0) C(1,-3) D(±,0)
X=sinΦ
2方程 (Φ为参数)所表示的曲线上一点的坐标是( )
Y=COSΦ
A(2,7) B(,) C(,) D(1,0)
X=1+2t
例2、已知曲线C的参数方程是 (t为参数,a R)
Y=at2
点M(5,4)在该C 曲线上。(1)求常数a ; (2)求曲线C的普通方程。
5=1+2t a=1
解:(1)由题意得 解得 ∴ a=1
4= at2 t=2
X=1+2t
(2)由已知(1)可得,曲线C的方程
Y=t2
由第一个方程得:t= ,代入第二个方程得 y= 所以(x-1)2=4y为所求。
思考题:动点M作等速直线运动, 它在x轴和y轴方向的速度分别为5和12 , 运动开始时位于点P(1,2), 求点M的轨迹参数方程。
X=1+5t
解:设动点M (x,y) 运动时间为t,依题意,得
Y=2+2t
X=1+5t
所以,点M的轨迹参数方程为
Y=2+12t
参数方程求法:
(1)建立直角坐标系, 设曲线上任一点P坐标为x,y
(2)选取适当的参数
(3)根据已知条件和图形的几何性质, 物理意义, 建立点P坐标与参数的函数式
(4)证明这个参数方程就是所由于的曲线的方程
四、小结:
一般地,在平面直角坐标系中,如果曲线上任意一点的坐标
X=f(t)
x,y都是某个变数t的函数 (2)
y=g(t)
并且对于t的每一个允许值,由方程组(2)所确定的点M(x,y)都在这条曲线上,那么方程(2)就叫做这条曲线的参数方程, 系变数x,y的变数t叫做参变数,简称参数。
五、作业P26习题 2.1 T1,T2,T3,T4
课题:曲线的参数方程
学 科:高 中 数 学
姓 名: 严 政
单 位:固镇县新马桥中学
2010年5月
oooo
500
提示:
即求飞行员在离救援点的水平距离
多远时,开始投放物资?
投放点
救援点
?
2010年教师资格
认定教学设计
解析几何初步
y
x
物资投出机舱后,它的运动由下列两种运动合成:
(1)沿ox作初速为100m/s的匀速直线运动;
(2)沿oy反方向作自由落体运动。
PAGE
5
同课章节目录
