2010北师大高中数学:点到直线的距离
文档属性
| 名称 | 2010北师大高中数学:点到直线的距离 |

|
|
| 格式 | rar | ||
| 文件大小 | 41.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-12 00:00:00 | ||
图片预览

文档简介
课 题:§1.5点到直线的距离公式
教学目标:
1、知识与技能
(1)让学生理解点到直线距离公式的推导过程 ,掌握点到直线距离公式及其简单应用;
(2)通过由特殊到一般的归纳,培养学生探索问题的能力。
2、过程与方法
(1)通过推导公式方法的发现,培养学生观察发现、分析归纳、抽象概括、数学表达等基本数学思维能力;
(2)在推导过程中,渗透数形结合、转化化归等数学思想以及特殊与一般的方法.
3、情感态度与价值观
引导学生用联系与转化的观点看问题,体验在探索问题的过程中的受挫感和成功感,培养合作意识和创新精神。同时感受数学的形式美与简洁美,从而激发学习兴趣。
教学重点: 点到直线距离公式和简单应用.
教学难点: 点到直线距离公式的推导.
教学方法: 小组讨论、合作探究学习,教师启发讲授。
教学手段: 多媒体教学。
教学过程:
一、复习回顾
前面几节课,我们一起研究学习了两直线的位置关系,两直线的交点问题,两点间的距离公式。逐步熟悉了利用代数方法研究几何问题的思想方法.
问:1. 两直线的位置关系?2. 两直线的交点情况?3. 两点间的距离公式?
二、创设情境,引入课题
如图,在铁路的附近,有一大型仓库.现要修建一条公路与之连接起来.那么怎样设计能使公路最短?最短路程又是多少?
这一节,我们将研究怎样由点的坐标和直线的方程直接求点P到直线的距离。
引例:计算点P(-3,5)到直线 : 3x-4y-5=0 的距离。
(学生讨论思考,教师引入课题)
三、探究新知
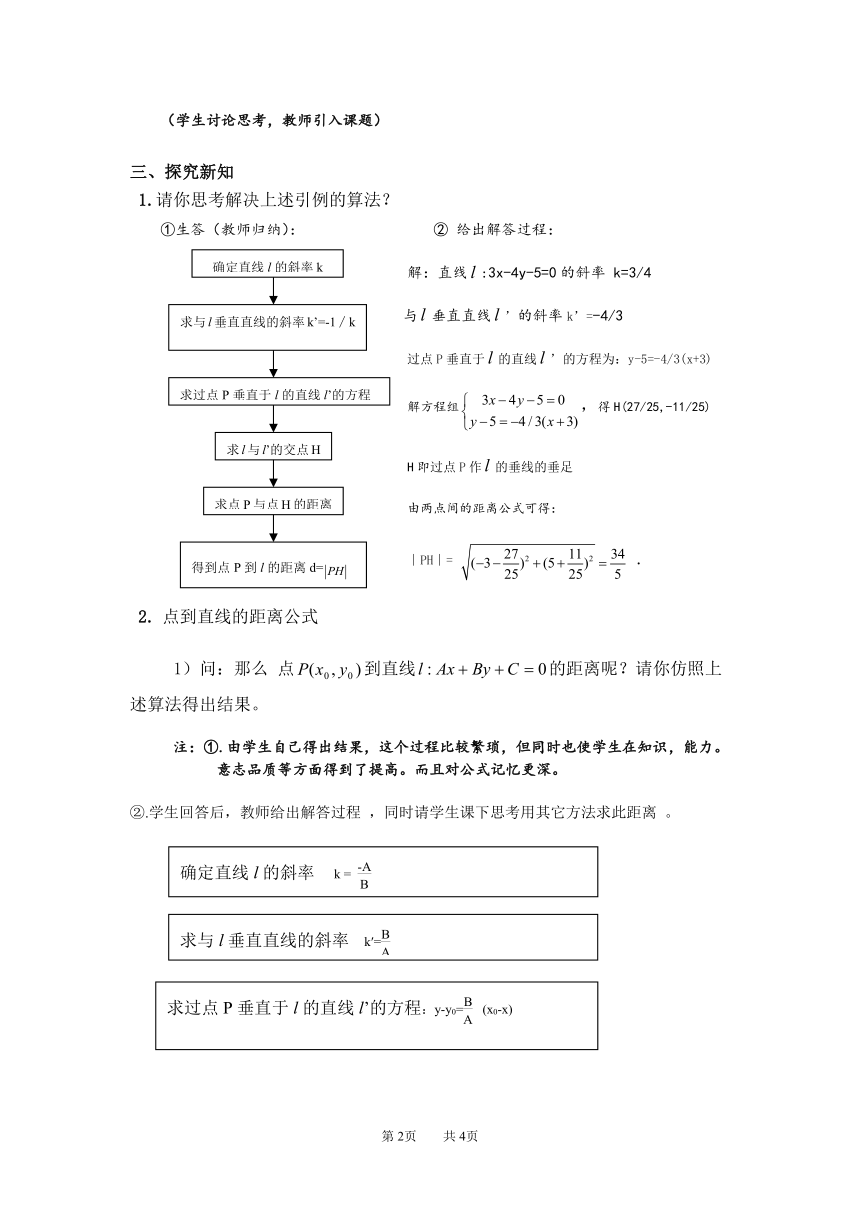
1.请你思考解决上述引例的算法?
①生答(教师归纳): ② 给出解答过程:
解:直线:3x-4y-5=0的斜率 k=3/4
与垂直直线’的斜率k’=-4/3
过点P垂直于的直线’的方程为:y-5=-4/3(x+3)
解方程组,得H(27/25,-11/25)
H即过点P作的垂线的垂足
由两点间的距离公式可得:
∣PH∣= .
2. 点到直线的距离公式
1)问:那么 点到直线的距离呢?请你仿照上述算法得出结果。
注:①.由学生自己得出结果,这个过程比较繁琐,但同时也使学生在知识,能力。意志品质等方面得到了提高。而且对公式记忆更深。
②.学生回答后,教师给出解答过程 ,同时请学生课下思考用其它方法求此距离 。
2)归纳:点到直线的距离公式
点到直线的距离公式的推导还有向量法,在必修4平面向量中利用向量法给出推导。
注:由学生回答,教师归纳,同时请同学验证引例的结果。
四、例题讲解
例1. (1)求原点到直线l1: 5x-12y-9=0的距离
(2)求点P(-1,2)到直线l2 : 2x+y-10=0的距离。
生答(教师归纳)
解:(1) 原点到直线l1的距离 d=
(2) 点P到直线l2 的距离d=
例2 .已知点A(1,3),B(3,1),C(-1,0),求三角形ABC的面积。
生答(教师归纳)
解:设AB边上的高为h,则S=
,
AB边上的高h就是点C到AB的距离。
AB边所在直线方程为 : , 即x+y-4=0。
点C到X+Y-4=0的距离为 : h= ,
因此,S=
注:通过这两道简单的例题,使学生能够进一步对点到直线的距离公式理解应用,能逐步体会用代数运算解决几何问题的优越性。
例3. 求平行线2x-7y+8=0和2x-7y-6=0的距离.
生答(教师归纳)
解:在直线2x-7y-6=0上任取一点,例如取P(3,0),则两平行线间的距离就是点P(3,0)到直线2x-7y+8=0的距离(图1-38).
注:要求学生能把求两平行线的距离转化为点到直线的距离公式
四、课堂练习:
P93 练习2 第1 , 2 题 .
五、小结 :
1.点到直线距离公式的推导过程,点到直线的距离公式,
2.能把求两平行线的距离转化为点到直线的距离公式
六、课后作业:
1.求点P(2,-1)到直线2+3-3=0的距离.
2.已知点A(,6)到直线3-4=2的距离d=4,求的值:
3.已知两条平行线直线和的一般式方程为:,
:,则与的距离为
七.板书设计:略
求过点P垂直于l的直线l’的方程:y-y0= EQ \F(B,A) (x0-x)
得到点P到l的距离d=
求点P与点H的距离
求l与l’的交点H
求过点P垂直于l的直线l’的方程
求与l垂直直线的斜率k’=-1∕k
得到点P到l的距离
求点P与点H的距离:
求l与l’的交点H(,)
求与l垂直直线的斜率 k′= EQ \F(B,A)
确定直线l的斜率 k = EQ \F(-A,B)
确定直线l的斜率k
铁路
仓库
第4页 共5页
教学目标:
1、知识与技能
(1)让学生理解点到直线距离公式的推导过程 ,掌握点到直线距离公式及其简单应用;
(2)通过由特殊到一般的归纳,培养学生探索问题的能力。
2、过程与方法
(1)通过推导公式方法的发现,培养学生观察发现、分析归纳、抽象概括、数学表达等基本数学思维能力;
(2)在推导过程中,渗透数形结合、转化化归等数学思想以及特殊与一般的方法.
3、情感态度与价值观
引导学生用联系与转化的观点看问题,体验在探索问题的过程中的受挫感和成功感,培养合作意识和创新精神。同时感受数学的形式美与简洁美,从而激发学习兴趣。
教学重点: 点到直线距离公式和简单应用.
教学难点: 点到直线距离公式的推导.
教学方法: 小组讨论、合作探究学习,教师启发讲授。
教学手段: 多媒体教学。
教学过程:
一、复习回顾
前面几节课,我们一起研究学习了两直线的位置关系,两直线的交点问题,两点间的距离公式。逐步熟悉了利用代数方法研究几何问题的思想方法.
问:1. 两直线的位置关系?2. 两直线的交点情况?3. 两点间的距离公式?
二、创设情境,引入课题
如图,在铁路的附近,有一大型仓库.现要修建一条公路与之连接起来.那么怎样设计能使公路最短?最短路程又是多少?
这一节,我们将研究怎样由点的坐标和直线的方程直接求点P到直线的距离。
引例:计算点P(-3,5)到直线 : 3x-4y-5=0 的距离。
(学生讨论思考,教师引入课题)
三、探究新知
1.请你思考解决上述引例的算法?
①生答(教师归纳): ② 给出解答过程:
解:直线:3x-4y-5=0的斜率 k=3/4
与垂直直线’的斜率k’=-4/3
过点P垂直于的直线’的方程为:y-5=-4/3(x+3)
解方程组,得H(27/25,-11/25)
H即过点P作的垂线的垂足
由两点间的距离公式可得:
∣PH∣= .
2. 点到直线的距离公式
1)问:那么 点到直线的距离呢?请你仿照上述算法得出结果。
注:①.由学生自己得出结果,这个过程比较繁琐,但同时也使学生在知识,能力。意志品质等方面得到了提高。而且对公式记忆更深。
②.学生回答后,教师给出解答过程 ,同时请学生课下思考用其它方法求此距离 。
2)归纳:点到直线的距离公式
点到直线的距离公式的推导还有向量法,在必修4平面向量中利用向量法给出推导。
注:由学生回答,教师归纳,同时请同学验证引例的结果。
四、例题讲解
例1. (1)求原点到直线l1: 5x-12y-9=0的距离
(2)求点P(-1,2)到直线l2 : 2x+y-10=0的距离。
生答(教师归纳)
解:(1) 原点到直线l1的距离 d=
(2) 点P到直线l2 的距离d=
例2 .已知点A(1,3),B(3,1),C(-1,0),求三角形ABC的面积。
生答(教师归纳)
解:设AB边上的高为h,则S=
,
AB边上的高h就是点C到AB的距离。
AB边所在直线方程为 : , 即x+y-4=0。
点C到X+Y-4=0的距离为 : h= ,
因此,S=
注:通过这两道简单的例题,使学生能够进一步对点到直线的距离公式理解应用,能逐步体会用代数运算解决几何问题的优越性。
例3. 求平行线2x-7y+8=0和2x-7y-6=0的距离.
生答(教师归纳)
解:在直线2x-7y-6=0上任取一点,例如取P(3,0),则两平行线间的距离就是点P(3,0)到直线2x-7y+8=0的距离(图1-38).
注:要求学生能把求两平行线的距离转化为点到直线的距离公式
四、课堂练习:
P93 练习2 第1 , 2 题 .
五、小结 :
1.点到直线距离公式的推导过程,点到直线的距离公式,
2.能把求两平行线的距离转化为点到直线的距离公式
六、课后作业:
1.求点P(2,-1)到直线2+3-3=0的距离.
2.已知点A(,6)到直线3-4=2的距离d=4,求的值:
3.已知两条平行线直线和的一般式方程为:,
:,则与的距离为
七.板书设计:略
求过点P垂直于l的直线l’的方程:y-y0= EQ \F(B,A) (x0-x)
得到点P到l的距离d=
求点P与点H的距离
求l与l’的交点H
求过点P垂直于l的直线l’的方程
求与l垂直直线的斜率k’=-1∕k
得到点P到l的距离
求点P与点H的距离:
求l与l’的交点H(,)
求与l垂直直线的斜率 k′= EQ \F(B,A)
确定直线l的斜率 k = EQ \F(-A,B)
确定直线l的斜率k
铁路
仓库
第4页 共5页
