15.2线段的垂直平分线 课件
图片预览








文档简介
课件20张PPT。15.2 线段的垂直平分线 安庆市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题1数学来源于生活又服务于生活你想从政吗?ABL实际问题2 在318国道L的同侧,有两个村庄A、B,为了便于两村庄的村民看病,镇政府计划在公路边上修建一所医院,使得两村的村民都没意见,问医院的院址应选在何处?318 国 道L数学来源于生活又服务于生活你想解决邻里纠纷吗1、什么是线段的垂直平分线?
2、如何作出一条线段的垂直平分线呢?
方法一:利用刻度尺和三角板找中点作垂直方法二:折纸操作法
在半透明的纸上画线段AB,折纸,使点A与点B重合,画出折痕CD.
在直线CD上任意取点E、F、P、Q,量一量EA和EB,FA和FB、PA和PB,QA和QB的长,你有什么发现?
想一想:(1)直线CD和线段AB有什么关系?
(2)直线CD上的点与点A点B又有什么关系?
根据(1)(2)你能猜想出什么结论?
做一做 想一想驶向胜利的彼岸结论:线段垂直平分线上的点到这条线段两个端点的距离相等。C驶向胜利的彼岸CPA=PB点P在线段AB的垂直平分线上线段垂直平分线上的点到这条线段两个端点的距离相等驶向胜利的彼岸 线段的垂直平分线C
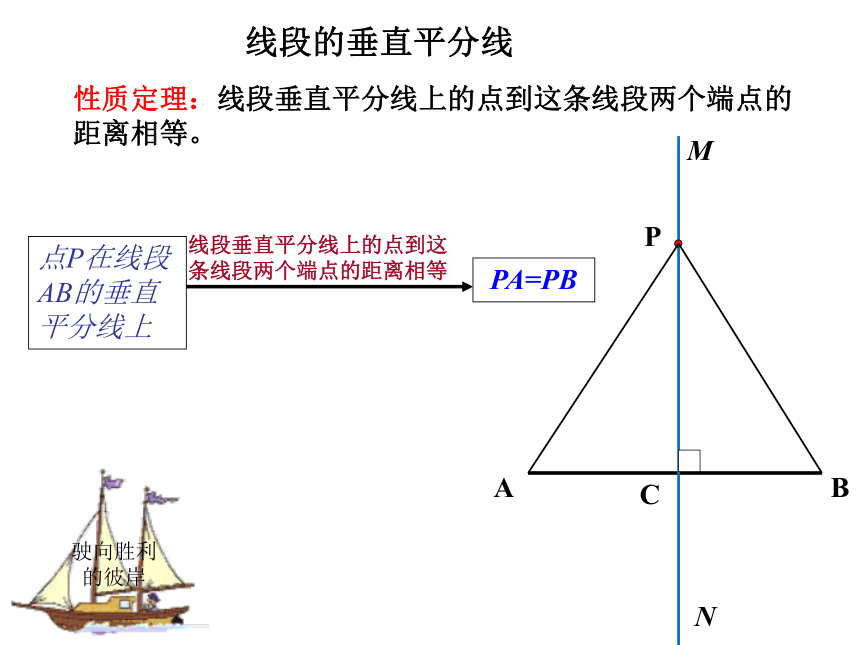
性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。PA=PB点P在线段AB的垂直平分线上?逆命题:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。由此你能想到用尺规如何作出线段的垂直平分线吗?
驶向胜利的彼岸驶向胜利的彼岸方法三:尺规作图已知:线段AB,如图.
求作:线段AB的垂直平分线.
作法:用尺规作线段的垂直平分线.1.分别以点A和B为圆心,以大于 AB长为半径作弧,两弧交于点C和D.2. 作直线CD.则直线CD就是线段AB的垂直平分线.请你说明CD为什么是AB的垂直平分线,并与同伴进行交流.老师提示:
因为直线CD与线段AB的交点就是AB的中点,所以我们也用这种方法作线段的中点.1—2二、逆定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。线段的垂直平分线一、性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。三、 线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是到线段两个端点距离相等的所有点的集合线段的垂直平分线例1 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC;驶向胜利的彼岸你能依据例1得到什么结论?结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。 安庆市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题1驶向胜利的彼岸线段的垂直平分线1、求作一点P,使它和△ABC的三个顶点距离相等.实际问题1驶向胜利的彼岸318 国 道ABL实际问题2 在国道L的同侧,有两个村庄A、B,为了便于两村的村民看病,镇政府计划在公路边上修建一所医院,使得两个村庄的村民都没意见,问医院的院址应选在何处?线段的垂直平分线2、如图,在直线L上求作一点P,使PA=PB.实际问题2数学问题源于生活实践,反过来数学又为生活实践服务教材130页
1、公路L同侧的A、B两村,共同出资在公路边修一个停靠站C,使停靠站到A、B两村距离相等,请你确定停靠站C的位置。练一练 我能行LAB驶向胜利的彼岸2、已知:直线L是线段AB的垂直平分线,C、D是L上任意两点(除AB的中点外)
求证:(1)△ABC、△ABD是等腰三角形
(2)∠ CAD= ∠CBD
3、已知:C、D是线段AB外两点,且 CA=CB,DA=DB.
求证:直线CD垂直平分线段AB 挑战自我驶向胜利的彼岸结束寄语证明的规范性在于:条理清晰,步步有理.这是初学证明者谨记和遵循的原则.
作业:教材 131页: 2、3、4
驶向胜利的彼岸
2、如何作出一条线段的垂直平分线呢?
方法一:利用刻度尺和三角板找中点作垂直方法二:折纸操作法
在半透明的纸上画线段AB,折纸,使点A与点B重合,画出折痕CD.
在直线CD上任意取点E、F、P、Q,量一量EA和EB,FA和FB、PA和PB,QA和QB的长,你有什么发现?
想一想:(1)直线CD和线段AB有什么关系?
(2)直线CD上的点与点A点B又有什么关系?
根据(1)(2)你能猜想出什么结论?
做一做 想一想驶向胜利的彼岸结论:线段垂直平分线上的点到这条线段两个端点的距离相等。C驶向胜利的彼岸CPA=PB点P在线段AB的垂直平分线上线段垂直平分线上的点到这条线段两个端点的距离相等驶向胜利的彼岸 线段的垂直平分线C
性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。PA=PB点P在线段AB的垂直平分线上?逆命题:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。由此你能想到用尺规如何作出线段的垂直平分线吗?
驶向胜利的彼岸驶向胜利的彼岸方法三:尺规作图已知:线段AB,如图.
求作:线段AB的垂直平分线.
作法:用尺规作线段的垂直平分线.1.分别以点A和B为圆心,以大于 AB长为半径作弧,两弧交于点C和D.2. 作直线CD.则直线CD就是线段AB的垂直平分线.请你说明CD为什么是AB的垂直平分线,并与同伴进行交流.老师提示:
因为直线CD与线段AB的交点就是AB的中点,所以我们也用这种方法作线段的中点.1—2二、逆定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。线段的垂直平分线一、性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。三、 线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是到线段两个端点距离相等的所有点的集合线段的垂直平分线例1 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC;驶向胜利的彼岸你能依据例1得到什么结论?结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。 安庆市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题1驶向胜利的彼岸线段的垂直平分线1、求作一点P,使它和△ABC的三个顶点距离相等.实际问题1驶向胜利的彼岸318 国 道ABL实际问题2 在国道L的同侧,有两个村庄A、B,为了便于两村的村民看病,镇政府计划在公路边上修建一所医院,使得两个村庄的村民都没意见,问医院的院址应选在何处?线段的垂直平分线2、如图,在直线L上求作一点P,使PA=PB.实际问题2数学问题源于生活实践,反过来数学又为生活实践服务教材130页
1、公路L同侧的A、B两村,共同出资在公路边修一个停靠站C,使停靠站到A、B两村距离相等,请你确定停靠站C的位置。练一练 我能行LAB驶向胜利的彼岸2、已知:直线L是线段AB的垂直平分线,C、D是L上任意两点(除AB的中点外)
求证:(1)△ABC、△ABD是等腰三角形
(2)∠ CAD= ∠CBD
3、已知:C、D是线段AB外两点,且 CA=CB,DA=DB.
求证:直线CD垂直平分线段AB 挑战自我驶向胜利的彼岸结束寄语证明的规范性在于:条理清晰,步步有理.这是初学证明者谨记和遵循的原则.
作业:教材 131页: 2、3、4
驶向胜利的彼岸
