10.3平行线的性质同步练习(沪科版七下)
文档属性
| 名称 | 10.3平行线的性质同步练习(沪科版七下) |

|
|
| 格式 | rar | ||
| 文件大小 | 37.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-10 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
10.3平行线的性质
一、基础过关:
1.下列语句中不是命题的有( )
(1)两点之间,直线最短;(2)不许大声讲话;
(3)连接A、B两点;(4)花儿在春天开放.
A.1个 B.2个 C.3个 D.4个
2.下列命题中,正确的是( )
A.在同一平面内,垂直于同一条直线的两条直线平行;
B.相等的角是对顶角;
C.两条直线被第三条直线所截,同位角相等;
D.和为180°的两个角叫做邻补角。
3.如图1,AB∥CD,AD,BC相交于O,∠BAD=35°,∠BOD=76°,则∠C的度数是 ( )
A.31° B.35° C.41° D.76°
(1) (2)
4.如图2,AB∥CD,AD∥BC,则下列各式中正确的是( )
A.∠1+∠2>∠3 B.∠1+∠2=∠3
C.∠1+∠2<∠3 D.∠1+∠2与∠3无关
5.请将下列命题改写成“如果……那么……”的形式:
(1)等角的余角相等;(2)垂直于同一条直线的两直线平行;
(3)平行线的同旁内角的平分线互相垂直.
6.下列命题的题设是什么?结论是什么?
(1)对顶角相等;(2)两条直线相交,只有一个交点;(3)如果a2=b2,那么a=b.
二、综合创新:
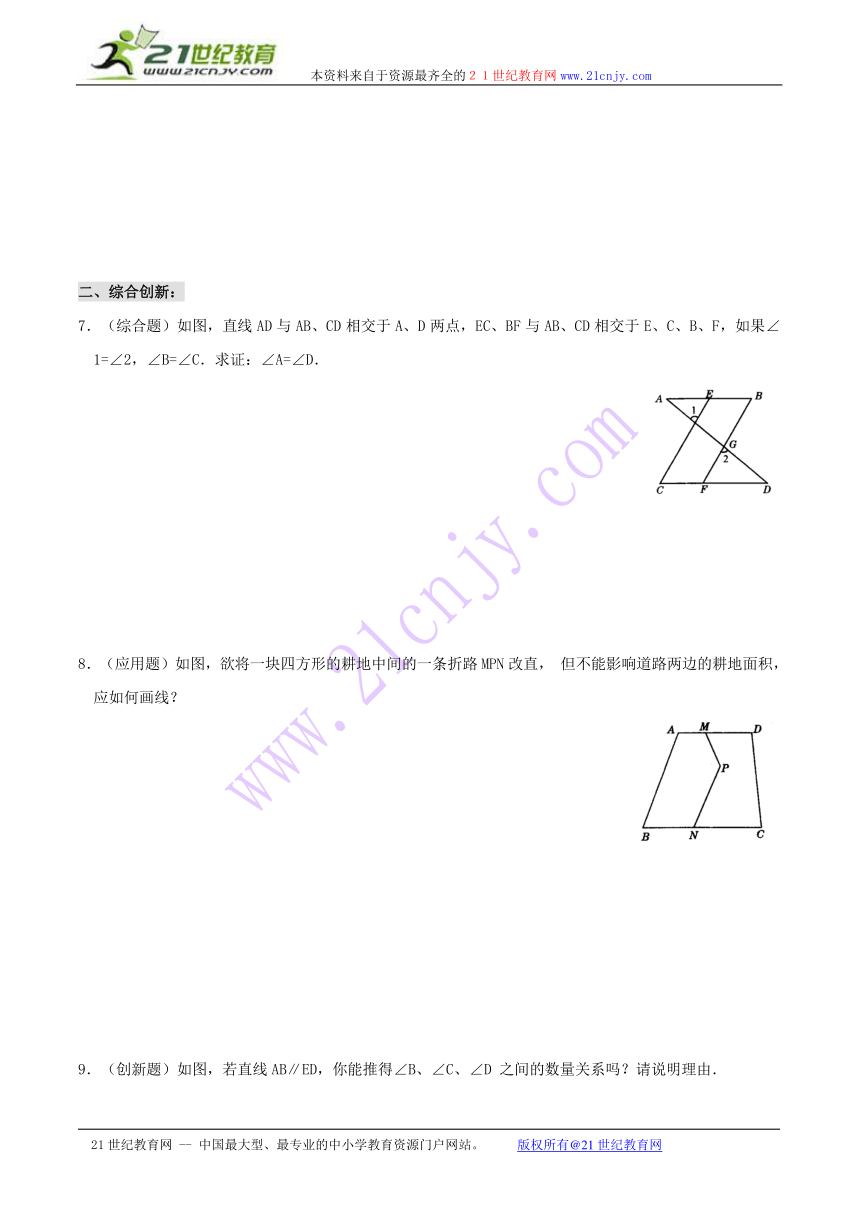
7.(综合题)如图,直线AD与AB、CD相交于A、D两点,EC、BF与AB、CD相交于E、C、B、F,如果∠1=∠2,∠B=∠C.求证:∠A=∠D.
8.(应用题)如图,欲将一块四方形的耕地中间的一条折路MPN改直,但不能影响道路两边的耕地面积,应如何画线?
9.(创新题)如图,若直线AB∥ED,你能推得∠B、∠C、∠D之间的数量关系吗?请说明理由.
10.(1)如图,已知AB∥CD,CE、AE分别平分∠ACD、∠CAB,则∠1+∠2______90°.(填“>”、“<”或“=”)
(3) (4)
(2)如图4,直线L1∥L 2,L3⊥L4,有三个命题:
①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4.下列说法中,正确的是 ( )
A.只有①正确 B.只有②正确; C.①和③正确 D.①②③都正确
三、名校培优:
11.(探究题)如图,已知AB∥CD,∠1=∠2,试探索∠BEF与∠EFC之间的关系,并说明理由.
12.(开放题)如果一个角的两边分别平行于另一个角的两边,那么这两个角之间有怎样的数量关系?请说明你的理由.
数学世界
抽屉原理
5个苹果放到4个抽屉里,必有一个抽屉里至少有两个苹果.
一般地,n+1个苹果放到n(n≥1)个抽屉里,必有一个抽屉里至少有两个苹果,这称为抽屉原理.
抽屉原理的应用很多.例如:在13个同学中,必有两个同学在同一个月过生日;10个客人住9个房间,必有两个客人住在同一个房间里.
想一想:在同一个圆内至少画几条半径,就必有两条半径的夹角小于60°?
参考答案
1.B 点拨:(2)、(3)不是命题.
2.A 3.C
4.B 点拨:∵AD∥BC,∴∠1=∠ACB.
∵AB∥CD,∴∠3=∠ACB+∠2=∠1+∠2.故选B.
5.解:(1)如果两个角相等,那么它们的余角相等.
(2)如果两条直线垂直于同一条直线,那么它们互相平行.
(3)如果两条射线分别是平行线的同旁内角的平分线,那么这两条射线互相垂直.
6.解:(1)题设:两个角是对顶角,结论:这两个角相等.
(2)题设:两条直线相交,结论:这两条直线只有一个交点.
(3)题设:a2=b2,结论:a=b.
7.证明:∵∠1=∠2,∠2=∠BGA(对顶角相等),
∴∠1=∠BGA.
∴CE∥BF.
∴∠B+∠BEC=180°.
又∵∠B=∠C,∴∠C+∠BEC=180°.
∴AB∥CD(同旁内角互补,两直线平行)
∴∠A=∠D(两直线平行,内错角相等).
8.连接MN.过P作EF∥MN交AD于E,BC于F.连接MF或NE,则MF或NE为新修的路.
9.解:∠C+∠D-∠B=180°.
理由:如答图,过点C作CF∥AB,则∠B=∠2.
∵AB∥ED,CF∥AB,
∴ED∥CF(平行于同一条直线的两直线平行).
∴∠1+∠D=180°(两直线平行,同旁内角互补).
而∠1=∠BCD-∠2=∠BCD-∠B,
∴∠BCD-∠B+∠D=180°,即∠BCD+∠D-∠B=180°.
点拨:平行线CF是联系AB、DE的桥梁.想一想,本题还有其他做法吗?
10.(1)=; (2)A。
11.解:∠BEF=∠EFC.
理由:如答图,分别延长BE、DC相交于点G.
∵AB∥CD,
∴∠1=∠G(两直线平行,内错角相等).
∵∠1=∠2,∴∠2=∠G,∴BE∥FC.
∴∠BEF=∠EFC(两直线平行,内错角相等).
12.解:这两个角相等或互补.
理由:如答图5-3-6,∠1与∠2、∠1与∠3的两边分别平行.
∵L1∥L2,L3∥L4,
∴∠1=∠4(两直线平行,内错角相等).
∠4=∠2.
∴∠1=∠2.
又∠2+∠3=180°.
∴∠1+∠3=180°.
从而∠1=∠2,∠1+∠3=180°.
点拨:分情况讨论是中考的常考内容,解答本题易因考虑不全面而出现错误.
数学世界(答案)
至少画7条半径.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
10.3平行线的性质
一、基础过关:
1.下列语句中不是命题的有( )
(1)两点之间,直线最短;(2)不许大声讲话;
(3)连接A、B两点;(4)花儿在春天开放.
A.1个 B.2个 C.3个 D.4个
2.下列命题中,正确的是( )
A.在同一平面内,垂直于同一条直线的两条直线平行;
B.相等的角是对顶角;
C.两条直线被第三条直线所截,同位角相等;
D.和为180°的两个角叫做邻补角。
3.如图1,AB∥CD,AD,BC相交于O,∠BAD=35°,∠BOD=76°,则∠C的度数是 ( )
A.31° B.35° C.41° D.76°
(1) (2)
4.如图2,AB∥CD,AD∥BC,则下列各式中正确的是( )
A.∠1+∠2>∠3 B.∠1+∠2=∠3
C.∠1+∠2<∠3 D.∠1+∠2与∠3无关
5.请将下列命题改写成“如果……那么……”的形式:
(1)等角的余角相等;(2)垂直于同一条直线的两直线平行;
(3)平行线的同旁内角的平分线互相垂直.
6.下列命题的题设是什么?结论是什么?
(1)对顶角相等;(2)两条直线相交,只有一个交点;(3)如果a2=b2,那么a=b.
二、综合创新:
7.(综合题)如图,直线AD与AB、CD相交于A、D两点,EC、BF与AB、CD相交于E、C、B、F,如果∠1=∠2,∠B=∠C.求证:∠A=∠D.
8.(应用题)如图,欲将一块四方形的耕地中间的一条折路MPN改直,但不能影响道路两边的耕地面积,应如何画线?
9.(创新题)如图,若直线AB∥ED,你能推得∠B、∠C、∠D之间的数量关系吗?请说明理由.
10.(1)如图,已知AB∥CD,CE、AE分别平分∠ACD、∠CAB,则∠1+∠2______90°.(填“>”、“<”或“=”)
(3) (4)
(2)如图4,直线L1∥L 2,L3⊥L4,有三个命题:
①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4.下列说法中,正确的是 ( )
A.只有①正确 B.只有②正确; C.①和③正确 D.①②③都正确
三、名校培优:
11.(探究题)如图,已知AB∥CD,∠1=∠2,试探索∠BEF与∠EFC之间的关系,并说明理由.
12.(开放题)如果一个角的两边分别平行于另一个角的两边,那么这两个角之间有怎样的数量关系?请说明你的理由.
数学世界
抽屉原理
5个苹果放到4个抽屉里,必有一个抽屉里至少有两个苹果.
一般地,n+1个苹果放到n(n≥1)个抽屉里,必有一个抽屉里至少有两个苹果,这称为抽屉原理.
抽屉原理的应用很多.例如:在13个同学中,必有两个同学在同一个月过生日;10个客人住9个房间,必有两个客人住在同一个房间里.
想一想:在同一个圆内至少画几条半径,就必有两条半径的夹角小于60°?
参考答案
1.B 点拨:(2)、(3)不是命题.
2.A 3.C
4.B 点拨:∵AD∥BC,∴∠1=∠ACB.
∵AB∥CD,∴∠3=∠ACB+∠2=∠1+∠2.故选B.
5.解:(1)如果两个角相等,那么它们的余角相等.
(2)如果两条直线垂直于同一条直线,那么它们互相平行.
(3)如果两条射线分别是平行线的同旁内角的平分线,那么这两条射线互相垂直.
6.解:(1)题设:两个角是对顶角,结论:这两个角相等.
(2)题设:两条直线相交,结论:这两条直线只有一个交点.
(3)题设:a2=b2,结论:a=b.
7.证明:∵∠1=∠2,∠2=∠BGA(对顶角相等),
∴∠1=∠BGA.
∴CE∥BF.
∴∠B+∠BEC=180°.
又∵∠B=∠C,∴∠C+∠BEC=180°.
∴AB∥CD(同旁内角互补,两直线平行)
∴∠A=∠D(两直线平行,内错角相等).
8.连接MN.过P作EF∥MN交AD于E,BC于F.连接MF或NE,则MF或NE为新修的路.
9.解:∠C+∠D-∠B=180°.
理由:如答图,过点C作CF∥AB,则∠B=∠2.
∵AB∥ED,CF∥AB,
∴ED∥CF(平行于同一条直线的两直线平行).
∴∠1+∠D=180°(两直线平行,同旁内角互补).
而∠1=∠BCD-∠2=∠BCD-∠B,
∴∠BCD-∠B+∠D=180°,即∠BCD+∠D-∠B=180°.
点拨:平行线CF是联系AB、DE的桥梁.想一想,本题还有其他做法吗?
10.(1)=; (2)A。
11.解:∠BEF=∠EFC.
理由:如答图,分别延长BE、DC相交于点G.
∵AB∥CD,
∴∠1=∠G(两直线平行,内错角相等).
∵∠1=∠2,∴∠2=∠G,∴BE∥FC.
∴∠BEF=∠EFC(两直线平行,内错角相等).
12.解:这两个角相等或互补.
理由:如答图5-3-6,∠1与∠2、∠1与∠3的两边分别平行.
∵L1∥L2,L3∥L4,
∴∠1=∠4(两直线平行,内错角相等).
∠4=∠2.
∴∠1=∠2.
又∠2+∠3=180°.
∴∠1+∠3=180°.
从而∠1=∠2,∠1+∠3=180°.
点拨:分情况讨论是中考的常考内容,解答本题易因考虑不全面而出现错误.
数学世界(答案)
至少画7条半径.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
