11.2 与三角形有关的角课件(2课时)
文档属性
| 名称 | 11.2 与三角形有关的角课件(2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 786.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-27 00:00:00 | ||
图片预览




文档简介
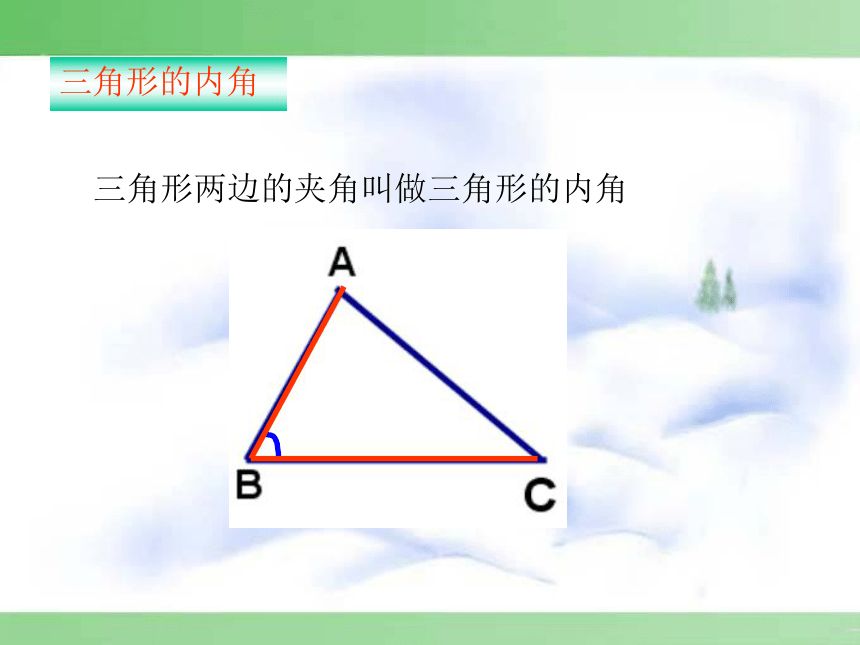
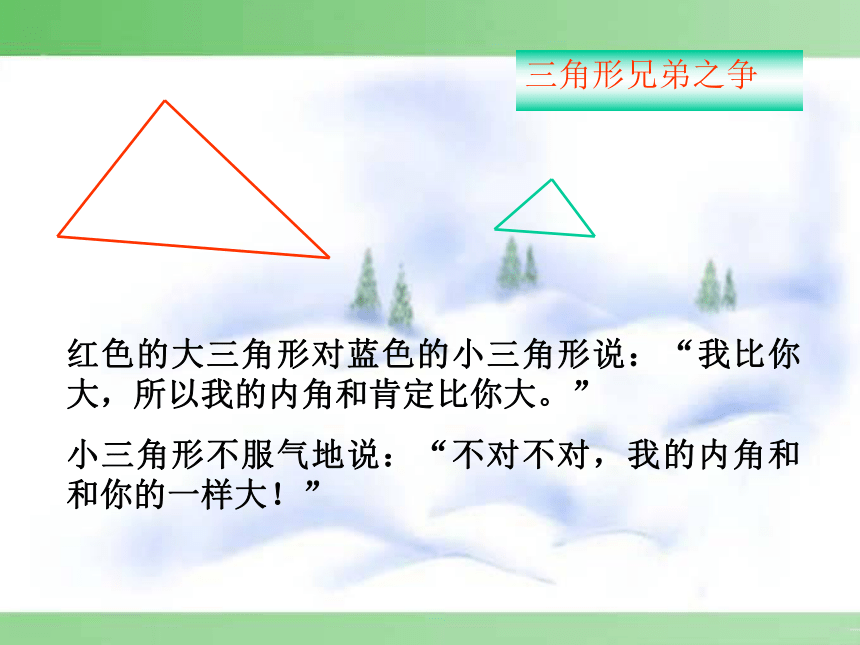
课件43张PPT。第十一章 三角形 11.2 与三角形有关的角11.2.1 三角形的内角三角形两边的夹角叫做三角形的内角三角形的内角红色的大三角形对蓝色的小三角形说:“我比你大,所以我的内角和肯定比你大。”
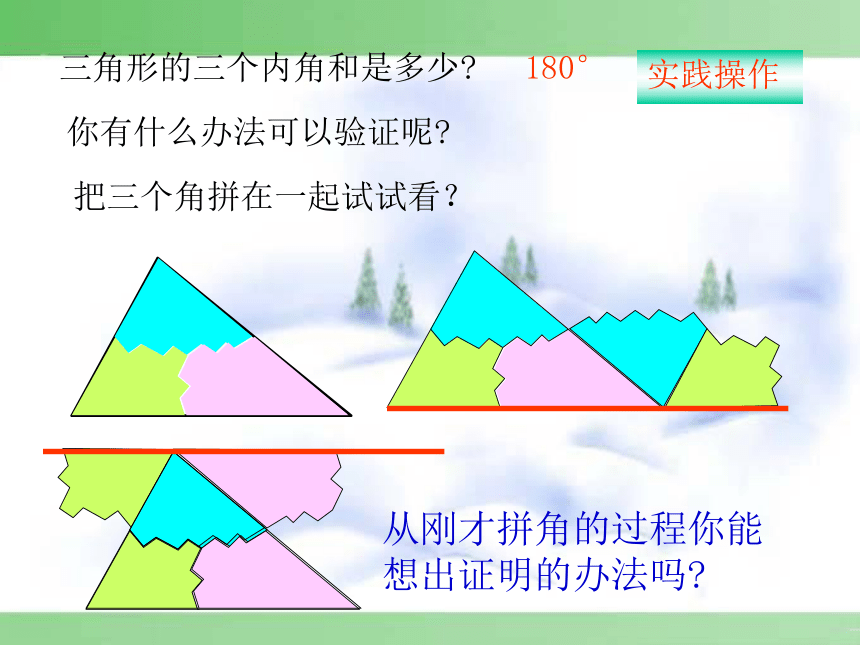
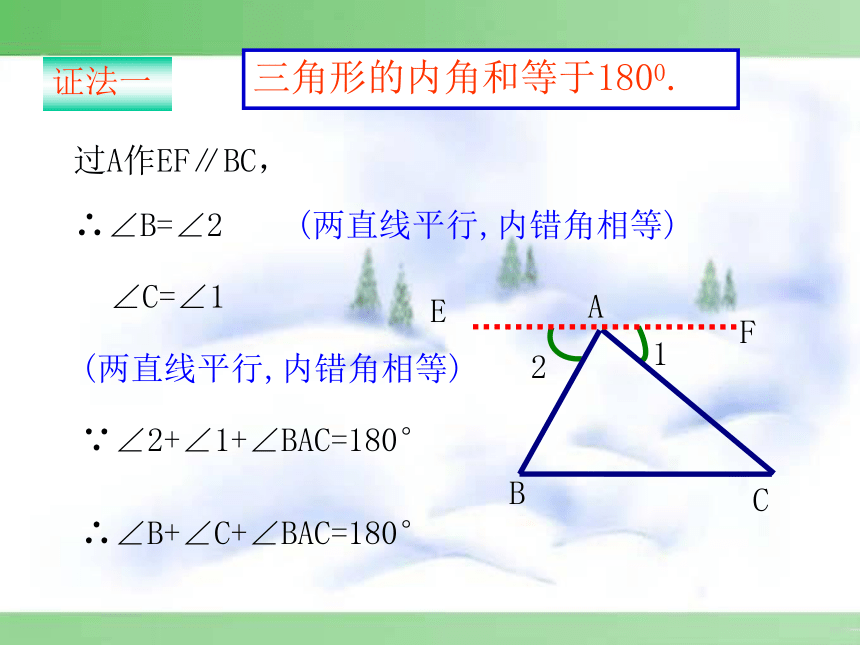
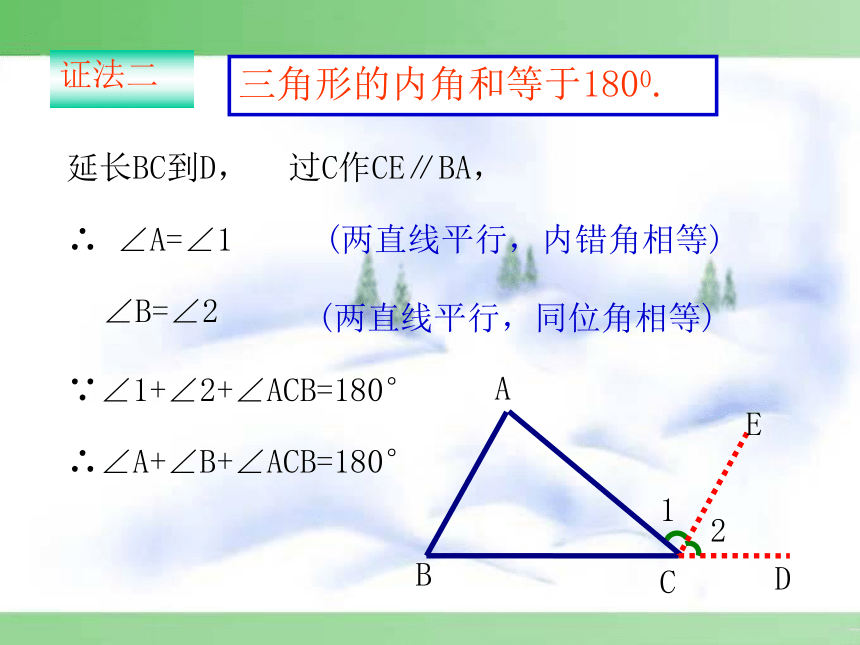
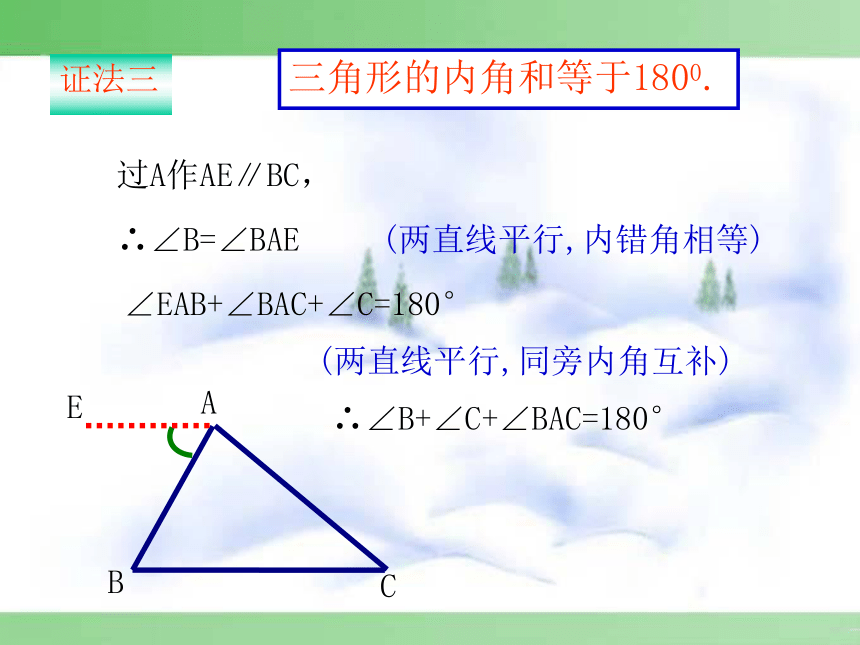
小三角形不服气地说:“不对不对,我的内角和和你的一样大!”三角形兄弟之争三角形的三个内角和是多少?把三个角拼在一起试试看?你有什么办法可以验证呢?从刚才拼角的过程你能想出证明的办法吗?180°实践操作F21ECBA三角形的内角和等于1800.过A作EF∥BC,∴∠B=∠2(两直线平行,内错角相等) ∠C=∠1(两直线平行,内错角相等) ∵∠2+∠1+∠BAC=180°∴∠B+∠C+∠BAC=180°证法一21EDCBA三角形的内角和等于1800.延长BC到D,过C作CE∥BA,∴ ∠A=∠1 (两直线平行,内错角相等)∠B=∠2(两直线平行,同位角相等)∵∠1+∠2+∠ACB=180°∴∠A+∠B+∠ACB=180°证法二CBEA三角形的内角和等于1800.过A作AE∥BC,∴∠B=∠BAE(两直线平行,内错角相等)∠EAB+∠BAC+∠C=180°(两直线平行,同旁内角互补)∴∠B+∠C+∠BAC=180°证法三 在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。 为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.思路总结(口答)下列各组角是同一个三角形的内角吗?为什么?(2)60°, 40°, 90°(3)30°, 60°, 50°(1)3°, 150°, 27° (是 )( 不是)( 不是)巩固练习(1)在△ABC中,∠A=35°,∠ B=43 °
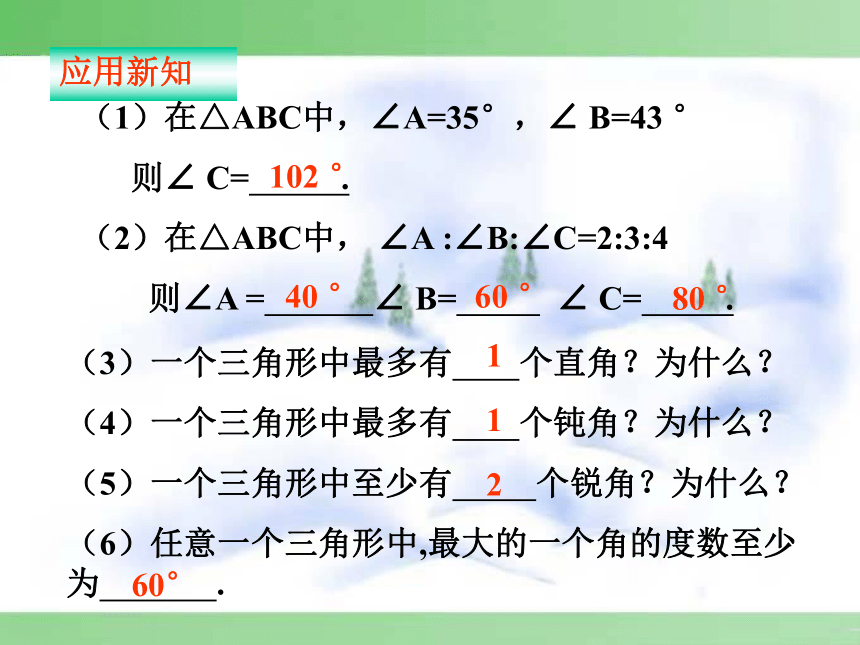
则∠ C= .
(2)在△ABC中, ∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C= . (3)一个三角形中最多有 个直角?为什么?
(4)一个三角形中最多有 个钝角?为什么?
(5)一个三角形中至少有 个锐角?为什么?
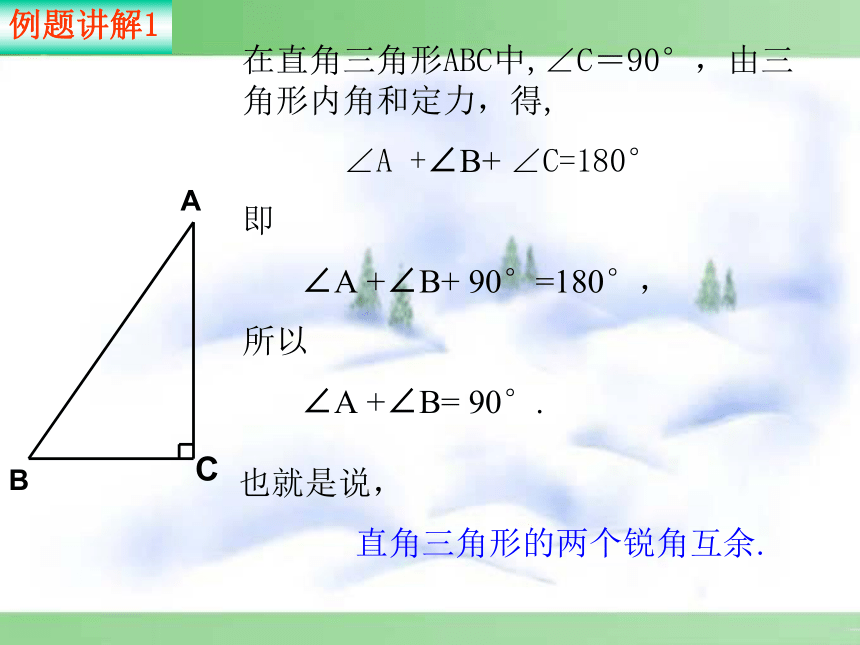
(6)任意一个三角形中,最大的一个角的度数至少为 .102 °80 °60 °40 °60°211应用新知ABC在直角三角形ABC中,∠C=90°,由三角形内角和定力,得,
∠A +∠B+ ∠C=180°
即
∠A +∠B+ 90°=180°,
所以
∠A +∠B= 90°.例题讲解1也就是说,
直角三角形的两个锐角互余.由三角形内角和定理可得:
有两个角互余的三角形是直角三角形。 直角三角形可以用符号“Rt△”表示,直角三角形ABC也可以写成Rt△ABC.ABC已知△ABC中,∠ABC=∠C=2∠A ,
BD是AC边上的高,求∠DBC的度数。解:设∠A=x0,则∠ABC=∠C=2x0∴x+2x+2x=180(三角形内角和定理)解得x=36∴∠C=2×360=720∴∠DBC=1800-900-720(三角形内角和定理)在△BDC中,∵∠BDC=900
(三角形高的定义)∴∠DBC=180?例题讲解2如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。求下面各题.(1)∠DAC=_____ ∠DAB=______ ∠EBC=_______ ∠CAB = ______ A(2)从C岛看A 、B两岛的视角∠C是多少?50°80°40°北解:∵ AD∥BE
∴ ∠DAB﹢∠ABE=180° ∴ ∠ABE = 180°-∠DAB = 180° - 80° =100° 在△ABC中,∠C = 180° - ∠CAB - ∠ABC= 180°-30 °-60 °=90°∴ ∠ABC=∠ABE﹣∠CBE30 °=100°﹣40°=60°例题讲解3DCE北A50°∟B40 °北MN在△AMC中 ∠AMC=90°, ∠MAC=50°解:过点C画MN⊥AD分别交AD、BE于点M、N12例:如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。∴∠1=180 °-90°-50° =40°∵ AD∥BE∴ ∠AMC+ ∠BNC =180 °∴ ∠BNC =90°同理得∠2 =50°∴ ∠ACB =180 ° -∠1 -∠2=180 °-40°-50° =90°例题讲解3B1250°40°解: 过点C画CF∥AD ∴ ∠1=∠DAC=50 °, F∵ CF∥AD, 又AD ∥BE∴ CF∥ BE∴∠2=∠CBE =40 °∴ ∠ACB=∠1﹢∠2 =50 °﹢ 40 ° =90 °例题讲解3巩固练习ABCDE如图,∠C= ∠D=90°,AD与BC相交于点E, ∠CAE和∠DBE什么关系。在Rt△ACE中, ∠CAE=90°- ∠AEC
在Rt△BDE中, ∠DBE=90°- ∠BED
∵ ∠AEC= ∠BED(对顶角相等)
∴ ∠CAE= ∠DBE3.△ABC中,若∠A+∠B=∠C,则△ABC是( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形4. 一个三角形至少有( )
A、一个锐角 B、两个锐角
C、一个钝角 D、一个直角BB巩固练习5. 如图△ABC中,CD平分∠ACB,DE∥BC,
∠A=70°,∠ADE=50°, 求∠BDC的度数.解:∵∠A=70° ∴∠ACB=180 °-∠A-∠B=180°-70°-50°=60°∵DE//BC∴∠B=∠ADE=50°∵ CD平分∠ACB巩固练习2、在△ABC中,如果∠A= ∠B= ∠ C,那么△ABC是什么三角形?解:设∠A=x°,那么∠B=2x°,∠C=3x°根据题意得:解得∴∠A=30°,∠B=60°,∠C=90°所以△ABC是直角三角形拓展与思考1甲楼高16米,乙楼座落在甲楼的正北面,已知当地冬至中午12点,太阳光线与水平面夹角为450,如果甲楼的影子刚好不落在乙楼上,那么两楼的距离应是多少?甲乙450?45016米解:由题意知ABC∴BC=AB=16答:两楼的距离是16米.拓展与思考2小结1、三角形的内角和:三角形三个内角之和为180°2、由三角形内角和等于180°,可得出(1)直角三角形两锐角互余;(2)一个三角形最多有一个直角或钝角;(3)任意一个三角形中,最多有三个锐角,最少有两个锐角;(4)一个三角形中至少有一个角小于或等于60°复习旧知一个三角形最多有 直角;
一个三角形最多有 钝角;
一个三角形中,最多有 锐角,最少有 锐角;
一个三角形中至少有一个角
小于或等于( )
一个三角形中最大角至少是( )
11.2.2 三角形的外角D三角形的外角: 三角形的一边与另一边的反向延长线组成的角.ABCDE看一看:算一算:探究?图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒⌒⌒⌒⌒115°60°65°55°125° 通过上题的计算,你发现∠ACD, ∠ CAE与三角形的内角之间有怎样的数量关系呢?请你试着用自己的语言说一说.想一想:三角形的一个外角等于与它不相邻的两个内角的和。结论:求下列各图中∠1的度数。∠1=∠1=∠1=90o85o95o ∠ACD ∠A (<、>);∠ACD ∠B (<、>)结论:三角形的一个外角大于任何一个与它不相 邻的内角。
D>>你选什么 ?把图中∠1、 ∠2、 ∠3按由大到小的顺序排列∠1∠2∠3>>三角形的外角和等于360°议一议∠2+ ∠ABC=180°∠3+ ∠ACB=180°三个式子相加得到∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°而∠BAC+ ∠ABC+∠ACB=180°∠1+ ∠2+ ∠3=360°解:过A作AD平行于BC∴ ∠3= ∠4BC123A∴ ∠2= ∠BAD∴ ∠1+ ∠2+ ∠3= ∠1+ ∠BAD+ ∠4=360°判断题:1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的外角和等于它内角和的2倍。( )
3、三角形的一个外角等于两个内角的和。( )
4、三角形的一个外角等于与它不相邻的两个内角的和。( )
5、三角形的一个外角大于任何一个内角。( )
6、三角形的一个内角小于任何一个与它不相邻的外角。( )练一练学一学例1:如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.问:(1)中为什么∠ADC=∠B+∠BAD?
(2)中求∠C的度数还有其他方法吗?40o40o⌒练一练∠A+∠B+∠C+∠D+∠E+∠F= .ADECFB123360°NPM(3)求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数⌒FG⌒∠B+ ∠D= ∠EGF∠EGF + ∠EFG + ∠E = 180°所以∠A+ ∠B+ ∠C+ ∠D+ ∠E= 180°练一练已知图中∠A、 ∠B、 ∠C分别为80°, 20° , 30° ,求∠1的度数如图,试计算∠BOC的度数.练一练90o30o20oABCOD⌒110°练一练如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°,
求∠A与∠EBC的度数.
小结1、三角形外角的两条性质① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
2、三角形的外角和是360
再见
小三角形不服气地说:“不对不对,我的内角和和你的一样大!”三角形兄弟之争三角形的三个内角和是多少?把三个角拼在一起试试看?你有什么办法可以验证呢?从刚才拼角的过程你能想出证明的办法吗?180°实践操作F21ECBA三角形的内角和等于1800.过A作EF∥BC,∴∠B=∠2(两直线平行,内错角相等) ∠C=∠1(两直线平行,内错角相等) ∵∠2+∠1+∠BAC=180°∴∠B+∠C+∠BAC=180°证法一21EDCBA三角形的内角和等于1800.延长BC到D,过C作CE∥BA,∴ ∠A=∠1 (两直线平行,内错角相等)∠B=∠2(两直线平行,同位角相等)∵∠1+∠2+∠ACB=180°∴∠A+∠B+∠ACB=180°证法二CBEA三角形的内角和等于1800.过A作AE∥BC,∴∠B=∠BAE(两直线平行,内错角相等)∠EAB+∠BAC+∠C=180°(两直线平行,同旁内角互补)∴∠B+∠C+∠BAC=180°证法三 在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。 为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.思路总结(口答)下列各组角是同一个三角形的内角吗?为什么?(2)60°, 40°, 90°(3)30°, 60°, 50°(1)3°, 150°, 27° (是 )( 不是)( 不是)巩固练习(1)在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
(2)在△ABC中, ∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C= . (3)一个三角形中最多有 个直角?为什么?
(4)一个三角形中最多有 个钝角?为什么?
(5)一个三角形中至少有 个锐角?为什么?
(6)任意一个三角形中,最大的一个角的度数至少为 .102 °80 °60 °40 °60°211应用新知ABC在直角三角形ABC中,∠C=90°,由三角形内角和定力,得,
∠A +∠B+ ∠C=180°
即
∠A +∠B+ 90°=180°,
所以
∠A +∠B= 90°.例题讲解1也就是说,
直角三角形的两个锐角互余.由三角形内角和定理可得:
有两个角互余的三角形是直角三角形。 直角三角形可以用符号“Rt△”表示,直角三角形ABC也可以写成Rt△ABC.ABC已知△ABC中,∠ABC=∠C=2∠A ,
BD是AC边上的高,求∠DBC的度数。解:设∠A=x0,则∠ABC=∠C=2x0∴x+2x+2x=180(三角形内角和定理)解得x=36∴∠C=2×360=720∴∠DBC=1800-900-720(三角形内角和定理)在△BDC中,∵∠BDC=900
(三角形高的定义)∴∠DBC=180?例题讲解2如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。求下面各题.(1)∠DAC=_____ ∠DAB=______ ∠EBC=_______ ∠CAB = ______ A(2)从C岛看A 、B两岛的视角∠C是多少?50°80°40°北解:∵ AD∥BE
∴ ∠DAB﹢∠ABE=180° ∴ ∠ABE = 180°-∠DAB = 180° - 80° =100° 在△ABC中,∠C = 180° - ∠CAB - ∠ABC= 180°-30 °-60 °=90°∴ ∠ABC=∠ABE﹣∠CBE30 °=100°﹣40°=60°例题讲解3DCE北A50°∟B40 °北MN在△AMC中 ∠AMC=90°, ∠MAC=50°解:过点C画MN⊥AD分别交AD、BE于点M、N12例:如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。∴∠1=180 °-90°-50° =40°∵ AD∥BE∴ ∠AMC+ ∠BNC =180 °∴ ∠BNC =90°同理得∠2 =50°∴ ∠ACB =180 ° -∠1 -∠2=180 °-40°-50° =90°例题讲解3B1250°40°解: 过点C画CF∥AD ∴ ∠1=∠DAC=50 °, F∵ CF∥AD, 又AD ∥BE∴ CF∥ BE∴∠2=∠CBE =40 °∴ ∠ACB=∠1﹢∠2 =50 °﹢ 40 ° =90 °例题讲解3巩固练习ABCDE如图,∠C= ∠D=90°,AD与BC相交于点E, ∠CAE和∠DBE什么关系。在Rt△ACE中, ∠CAE=90°- ∠AEC
在Rt△BDE中, ∠DBE=90°- ∠BED
∵ ∠AEC= ∠BED(对顶角相等)
∴ ∠CAE= ∠DBE3.△ABC中,若∠A+∠B=∠C,则△ABC是( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形4. 一个三角形至少有( )
A、一个锐角 B、两个锐角
C、一个钝角 D、一个直角BB巩固练习5. 如图△ABC中,CD平分∠ACB,DE∥BC,
∠A=70°,∠ADE=50°, 求∠BDC的度数.解:∵∠A=70° ∴∠ACB=180 °-∠A-∠B=180°-70°-50°=60°∵DE//BC∴∠B=∠ADE=50°∵ CD平分∠ACB巩固练习2、在△ABC中,如果∠A= ∠B= ∠ C,那么△ABC是什么三角形?解:设∠A=x°,那么∠B=2x°,∠C=3x°根据题意得:解得∴∠A=30°,∠B=60°,∠C=90°所以△ABC是直角三角形拓展与思考1甲楼高16米,乙楼座落在甲楼的正北面,已知当地冬至中午12点,太阳光线与水平面夹角为450,如果甲楼的影子刚好不落在乙楼上,那么两楼的距离应是多少?甲乙450?45016米解:由题意知ABC∴BC=AB=16答:两楼的距离是16米.拓展与思考2小结1、三角形的内角和:三角形三个内角之和为180°2、由三角形内角和等于180°,可得出(1)直角三角形两锐角互余;(2)一个三角形最多有一个直角或钝角;(3)任意一个三角形中,最多有三个锐角,最少有两个锐角;(4)一个三角形中至少有一个角小于或等于60°复习旧知一个三角形最多有 直角;
一个三角形最多有 钝角;
一个三角形中,最多有 锐角,最少有 锐角;
一个三角形中至少有一个角
小于或等于( )
一个三角形中最大角至少是( )
11.2.2 三角形的外角D三角形的外角: 三角形的一边与另一边的反向延长线组成的角.ABCDE看一看:算一算:探究?图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒⌒⌒⌒⌒115°60°65°55°125° 通过上题的计算,你发现∠ACD, ∠ CAE与三角形的内角之间有怎样的数量关系呢?请你试着用自己的语言说一说.想一想:三角形的一个外角等于与它不相邻的两个内角的和。结论:求下列各图中∠1的度数。∠1=∠1=∠1=90o85o95o ∠ACD ∠A (<、>);∠ACD ∠B (<、>)结论:三角形的一个外角大于任何一个与它不相 邻的内角。
D>>你选什么 ?把图中∠1、 ∠2、 ∠3按由大到小的顺序排列∠1∠2∠3>>三角形的外角和等于360°议一议∠2+ ∠ABC=180°∠3+ ∠ACB=180°三个式子相加得到∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°而∠BAC+ ∠ABC+∠ACB=180°∠1+ ∠2+ ∠3=360°解:过A作AD平行于BC∴ ∠3= ∠4BC123A∴ ∠2= ∠BAD∴ ∠1+ ∠2+ ∠3= ∠1+ ∠BAD+ ∠4=360°判断题:1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的外角和等于它内角和的2倍。( )
3、三角形的一个外角等于两个内角的和。( )
4、三角形的一个外角等于与它不相邻的两个内角的和。( )
5、三角形的一个外角大于任何一个内角。( )
6、三角形的一个内角小于任何一个与它不相邻的外角。( )练一练学一学例1:如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.问:(1)中为什么∠ADC=∠B+∠BAD?
(2)中求∠C的度数还有其他方法吗?40o40o⌒练一练∠A+∠B+∠C+∠D+∠E+∠F= .ADECFB123360°NPM(3)求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数⌒FG⌒∠B+ ∠D= ∠EGF∠EGF + ∠EFG + ∠E = 180°所以∠A+ ∠B+ ∠C+ ∠D+ ∠E= 180°练一练已知图中∠A、 ∠B、 ∠C分别为80°, 20° , 30° ,求∠1的度数如图,试计算∠BOC的度数.练一练90o30o20oABCOD⌒110°练一练如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°,
求∠A与∠EBC的度数.
小结1、三角形外角的两条性质① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
2、三角形的外角和是360
再见
