1.1.2 简单多面体 学案1(含答案)
文档属性
| 名称 | 1.1.2 简单多面体 学案1(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 11.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-28 00:00:00 | ||
图片预览


文档简介
1.1.2 简单多面体
学案
学习目标
重点难点
1.通过实物操作,增强学生的直观感知.2.能根据几何体的结构特征对空间物体进行分类.3.会用语言概述棱柱、棱锥、棱台、简单组合体的结构特征.4.会表示有关几何体以及柱、锥、台的分类.
重点:感受大量空间实物及模型,概括出棱柱、棱锥、棱台、简单组合体的结构特征.难点:棱柱、棱锥、棱台、简单组合体的结构特征的概括与简单计算.疑点:棱柱、棱锥、棱台的结构特征的理解.
1.多面体
我们把若干个平面多边形围成的几何体叫作多面体.其中棱柱、棱锥、棱台都是简单多面体.
2.棱柱
两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫棱柱.棱柱的侧面是平行四边形.
预习交流1
棱柱是“有两个面是互相平行且全等的多边形,其余各面都是平行四边形的多面体”.这一概念对吗?为什么?
提示:不对.如图,是由两个三棱柱叠放在一起形成的几何体,这个几何体不是棱柱.这是因为虽然上、下面平行,但是四边形ABB1A1与四边形A1B1B2A2不在一个平面内,
所以多边形ABB1B2A2A1不是一个平面图形,它更不是一个平行四边形,因此这个几何体不是一个棱柱.
所以棱柱的定义中强调“其余各面是四边形,且每相邻两个四边形的公共边都互相平行”.
预习交流2
什么是直棱柱?什么是正棱柱?两者有什么区别?
提示:侧棱垂直于底面的棱柱叫作直棱柱,底面是正多边形的直棱柱叫作正棱柱.
直棱柱与正棱柱的区别
①直棱柱是在一般棱柱的基础上加一个条件“侧棱与底面垂直”;
②正棱柱是在直棱柱的基础上加一个条件“底面是正多边形”.
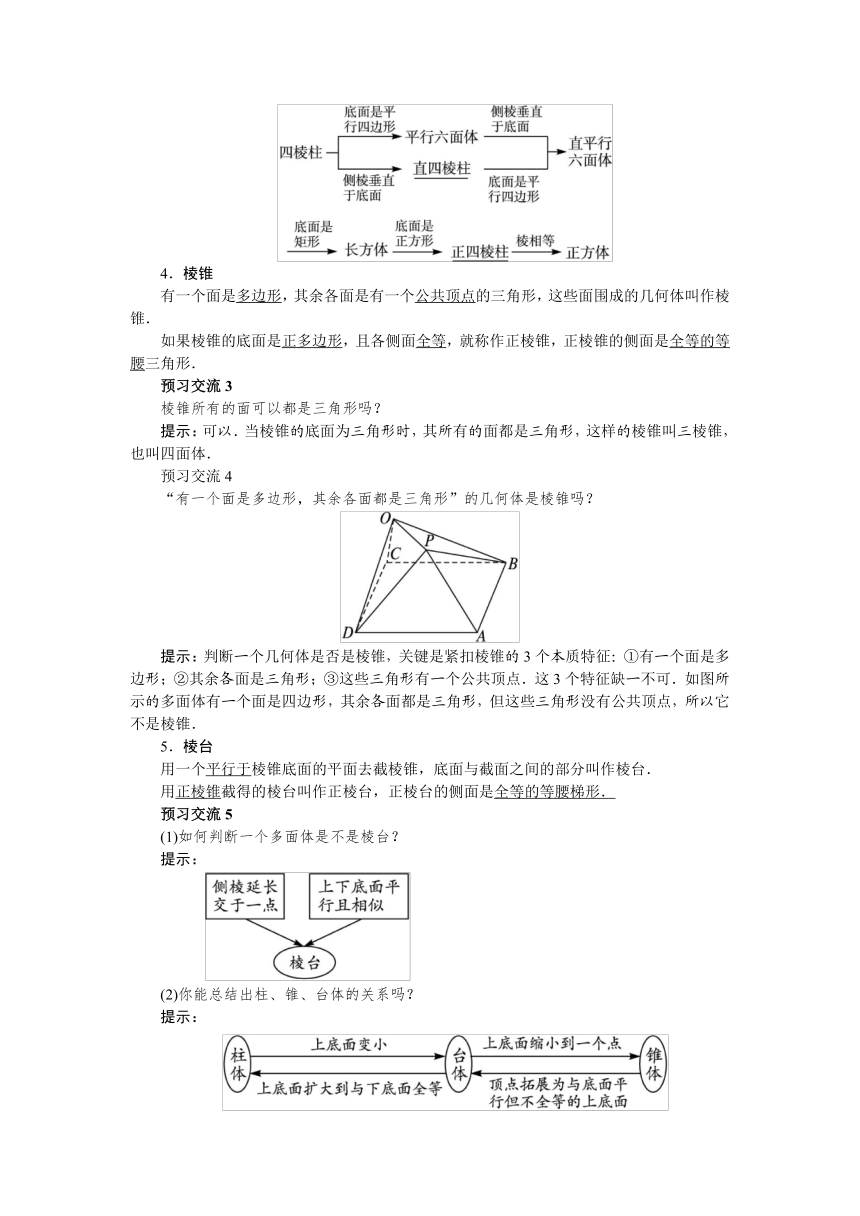
3.特殊的四棱柱
4.棱锥
有一个面是多边形,其余各面是有一个公共顶点的三角形,这些面围成的几何体叫作棱锥.
如果棱锥的底面是正多边形,且各侧面全等,就称作正棱锥,正棱锥的侧面是全等的等腰三角形.
预习交流3
棱锥所有的面可以都是三角形吗?
提示:可以.当棱锥的底面为三角形时,其所有的面都是三角形,这样的棱锥叫三棱锥,也叫四面体.
预习交流4
“有一个面是多边形,其余各面都是三角形”的几何体是棱锥吗?
提示:判断一个几何体是否是棱锥,关键是紧扣棱锥的3个本质特征:①有一个面是多边形;②其余各面是三角形;③这些三角形有一个公共顶点.这3个特征缺一不可.如图所示的多面体有一个面是四边形,其余各面都是三角形,但这些三角形没有公共顶点,所以它不是棱锥.
5.棱台
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫作棱台.
用正棱锥截得的棱台叫作正棱台,正棱台的侧面是全等的等腰梯形.
预习交流5
(1)如何判断一个多面体是不是棱台?
提示:
(2)你能总结出柱、锥、台体的关系吗?
提示:
1.对简单多面体的理解
如图所示为长方体ABCD A′B′C′D′,当用平面BCFE把这个长方体分成两部分后,各部分形成的多面体还是棱柱吗?如果不是,请说明理由;如果是,指出底面及侧棱.
思路分析:①本题是一个几何体的分割问题;
②分割后是两个几何体.
解题时可先确定两个互相平行的面,然后根据棱柱的定义得出结论.
解:截面BCFE上方部分是棱柱BB′E CC′F,其中平面BB′E和平面CC′F是其底面,BC,B′C′,EF是其侧棱.
截面BCFE下方部分是棱柱ABEA′ DCFD′,其中平面ABEA′和DCFD′是其底面,AD,BC,EF,A′D′是其侧棱.
给出下列几个结论:
①长方体一定是正四棱柱;
②棱锥的侧面为三角形,且所有侧面都有一个公共顶点;
③多面体至少有四个面;
④棱台的侧棱所在直线均相交于同一点.
其中,错误的个数是( ).
A.0
B.1
C.2
D.3
思路分析:解答本题的依据是棱柱、棱锥、棱台的结构特征,结合已知进行具体分析.
解析:对于①,长方体的底面不一定是正方形,故①错;②显然是正确的;对于③,一个图形要成为空间几何体,至少需有四个顶点,当有四个顶点时,易知它可围成四个面,因而一个多面体至少应有四个面,而且这样的面必是三角形,故③是正确的;对于④,棱台的侧棱所在的直线就是所截棱锥的侧棱所在的直线,而棱锥的侧棱都有一个公共的点,即棱锥的顶点,于是棱台的侧棱所在直线均相交于同一点,故④是正确的.
答案:B
1.下列命题中,正确的是( ).
A.棱柱中互相平行的两个面叫作棱柱的底面
B.棱柱的侧面是平行四边形,而底面不是平行四边形
C.棱柱的侧棱都相等,侧面都是平行四边形
D.侧棱与底面两边垂直的棱柱叫直棱柱
解析:在棱柱底面的定义中,两个互相平行的面是特指的,反之,则不一定,如底面是梯形时,有两个侧面互相平行,这两个平行的侧面就不能称为棱柱的底面,故A不正确;棱柱可以是平行六面体,所以B项不正确,C正确;由直棱柱的定义知D错误.
答案:C
2.下列说法正确的有( ).
①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;
②两个底面平行且相似,其余各面都是梯形的多面体是棱台;
③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.
A.0个
B.1个
C.2个
D.3个
解析:①中的平面不一定平行于底面,故①错;②③可用反例(如下图所示)加以检验,故②③均不对.
答案:A
认识一个几何体的结构特征,主要从它的侧面、侧棱、底面等角度描述,因此只有理解并掌握好各几何体的概念,才能认清其属性.
2.简单多面体有关量的计算
已知正三棱锥V ABC中,底面边长为8,侧棱长为,计算它的高和斜高.
思路分析:本题主要考查正三棱锥中基本量的计算,关键是把已知量与未知量放到直角三角形中求解.
解:如图所示,设O是底面中心,则D为BC的中点,
∴△VAO和△VCD都是直角三角形.
∵底面边长为8,侧棱长为2,
∴AO=×8=,CD=4,
∴VO===.
VD===2.
即正三棱锥的高是,斜高为2.
正三棱台的上、下底面边长分别为3和6,高为1,试求该棱台的侧棱和斜高.
解:如图,设上、下两底的中心分别是O1,O,连接O1O,则O1O为棱台的高,O1O=1.连接A1O1,AO并延长分别与B1C1和BC相交于D1,D.由平面几何知识得,D1,D分别是B1C1和BC的中点,连接D1D,则D1D为棱台的斜高.
因为B1C1=3,BC=6,所以A1O1=×3=,AO=×6=2,O1D1=×3=,OD=×6=.
在直角梯形AOO1A1中,A1A==2;
在直角梯形DOO1D1中,D1D==.
即该棱台的侧棱和斜高分别为2和.
正棱锥中基本量的计算要借助构造的直角三角形,如[活动与探究3]中的Rt△VAO,Rt△VOD,Rt△VCD等.它们包含了正棱锥的侧棱长、高、斜高、底面边长的一半,底面外接圆半径和内切圆半径.
类似地,在正棱台中,有三个重要的直角梯形——两底面中心连线、相应的边心距和斜高组成一个直角梯形;两底面中心连线、侧棱和相应两底面正多边形的顶点与中心连线组成一个直角梯形;斜高、侧棱和上下两底面边长的一半组成一个直角梯形.正棱台的计算问题,实际上就是这几个直角梯形的计算问题.
1.在棱柱中( ).
A.只有两个面平行
B.所有的棱都平行
C.所有的面都是平行四边形
D.两底面平行,且各侧棱也互相平行
答案:D
2.棱柱的侧面都是( ).
A.三角形
B.四边形
C.五边形
D.矩形
答案:B
3.从长方体的一个顶点出发的三条棱上各取一点E,F,G,过此三点作长方体的截面,那么截去的几何体是( ).
A.三棱柱
B.三棱锥
C.四棱柱
D.四棱锥
答案:B
4.下列描述中,是棱台的性质的是__________.(填序号)
①两底面平行;②侧面都是梯形;③侧棱都相等,且平行;④侧棱延长后都交于一点;⑤底面不可能为三角形.
解析:棱台是由棱锥截得的,截面与底面平行,①正确;棱台的侧面都是梯形,②正确;③错误;棱台侧棱延长后必交于一点,④正确;由三棱锥截得的棱台为三棱台,其底面是三角形,⑤错误.
答案:①②④
5.判断下列语句的对错.
(1)一个棱锥至少有四个面;
(2)如果四棱锥的底面是正方形,那么这个四棱锥的四条侧棱都相等;
(3)五棱锥只有五条棱;
(4)用与底面平行的平面去截三棱锥,得到的截面三角形和底面三角形相似.
解:(1)正确;
(2)不正确,四棱锥的底面是正方形,它的侧棱可以相等,也可以不相等;
(3)不正确,五棱锥除了五条侧棱外,还有五条底边,故共有10条棱;
(4)正确.
学案
学习目标
重点难点
1.通过实物操作,增强学生的直观感知.2.能根据几何体的结构特征对空间物体进行分类.3.会用语言概述棱柱、棱锥、棱台、简单组合体的结构特征.4.会表示有关几何体以及柱、锥、台的分类.
重点:感受大量空间实物及模型,概括出棱柱、棱锥、棱台、简单组合体的结构特征.难点:棱柱、棱锥、棱台、简单组合体的结构特征的概括与简单计算.疑点:棱柱、棱锥、棱台的结构特征的理解.
1.多面体
我们把若干个平面多边形围成的几何体叫作多面体.其中棱柱、棱锥、棱台都是简单多面体.
2.棱柱
两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫棱柱.棱柱的侧面是平行四边形.
预习交流1
棱柱是“有两个面是互相平行且全等的多边形,其余各面都是平行四边形的多面体”.这一概念对吗?为什么?
提示:不对.如图,是由两个三棱柱叠放在一起形成的几何体,这个几何体不是棱柱.这是因为虽然上、下面平行,但是四边形ABB1A1与四边形A1B1B2A2不在一个平面内,
所以多边形ABB1B2A2A1不是一个平面图形,它更不是一个平行四边形,因此这个几何体不是一个棱柱.
所以棱柱的定义中强调“其余各面是四边形,且每相邻两个四边形的公共边都互相平行”.
预习交流2
什么是直棱柱?什么是正棱柱?两者有什么区别?
提示:侧棱垂直于底面的棱柱叫作直棱柱,底面是正多边形的直棱柱叫作正棱柱.
直棱柱与正棱柱的区别
①直棱柱是在一般棱柱的基础上加一个条件“侧棱与底面垂直”;
②正棱柱是在直棱柱的基础上加一个条件“底面是正多边形”.
3.特殊的四棱柱
4.棱锥
有一个面是多边形,其余各面是有一个公共顶点的三角形,这些面围成的几何体叫作棱锥.
如果棱锥的底面是正多边形,且各侧面全等,就称作正棱锥,正棱锥的侧面是全等的等腰三角形.
预习交流3
棱锥所有的面可以都是三角形吗?
提示:可以.当棱锥的底面为三角形时,其所有的面都是三角形,这样的棱锥叫三棱锥,也叫四面体.
预习交流4
“有一个面是多边形,其余各面都是三角形”的几何体是棱锥吗?
提示:判断一个几何体是否是棱锥,关键是紧扣棱锥的3个本质特征:①有一个面是多边形;②其余各面是三角形;③这些三角形有一个公共顶点.这3个特征缺一不可.如图所示的多面体有一个面是四边形,其余各面都是三角形,但这些三角形没有公共顶点,所以它不是棱锥.
5.棱台
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫作棱台.
用正棱锥截得的棱台叫作正棱台,正棱台的侧面是全等的等腰梯形.
预习交流5
(1)如何判断一个多面体是不是棱台?
提示:
(2)你能总结出柱、锥、台体的关系吗?
提示:
1.对简单多面体的理解
如图所示为长方体ABCD A′B′C′D′,当用平面BCFE把这个长方体分成两部分后,各部分形成的多面体还是棱柱吗?如果不是,请说明理由;如果是,指出底面及侧棱.
思路分析:①本题是一个几何体的分割问题;
②分割后是两个几何体.
解题时可先确定两个互相平行的面,然后根据棱柱的定义得出结论.
解:截面BCFE上方部分是棱柱BB′E CC′F,其中平面BB′E和平面CC′F是其底面,BC,B′C′,EF是其侧棱.
截面BCFE下方部分是棱柱ABEA′ DCFD′,其中平面ABEA′和DCFD′是其底面,AD,BC,EF,A′D′是其侧棱.
给出下列几个结论:
①长方体一定是正四棱柱;
②棱锥的侧面为三角形,且所有侧面都有一个公共顶点;
③多面体至少有四个面;
④棱台的侧棱所在直线均相交于同一点.
其中,错误的个数是( ).
A.0
B.1
C.2
D.3
思路分析:解答本题的依据是棱柱、棱锥、棱台的结构特征,结合已知进行具体分析.
解析:对于①,长方体的底面不一定是正方形,故①错;②显然是正确的;对于③,一个图形要成为空间几何体,至少需有四个顶点,当有四个顶点时,易知它可围成四个面,因而一个多面体至少应有四个面,而且这样的面必是三角形,故③是正确的;对于④,棱台的侧棱所在的直线就是所截棱锥的侧棱所在的直线,而棱锥的侧棱都有一个公共的点,即棱锥的顶点,于是棱台的侧棱所在直线均相交于同一点,故④是正确的.
答案:B
1.下列命题中,正确的是( ).
A.棱柱中互相平行的两个面叫作棱柱的底面
B.棱柱的侧面是平行四边形,而底面不是平行四边形
C.棱柱的侧棱都相等,侧面都是平行四边形
D.侧棱与底面两边垂直的棱柱叫直棱柱
解析:在棱柱底面的定义中,两个互相平行的面是特指的,反之,则不一定,如底面是梯形时,有两个侧面互相平行,这两个平行的侧面就不能称为棱柱的底面,故A不正确;棱柱可以是平行六面体,所以B项不正确,C正确;由直棱柱的定义知D错误.
答案:C
2.下列说法正确的有( ).
①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;
②两个底面平行且相似,其余各面都是梯形的多面体是棱台;
③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.
A.0个
B.1个
C.2个
D.3个
解析:①中的平面不一定平行于底面,故①错;②③可用反例(如下图所示)加以检验,故②③均不对.
答案:A
认识一个几何体的结构特征,主要从它的侧面、侧棱、底面等角度描述,因此只有理解并掌握好各几何体的概念,才能认清其属性.
2.简单多面体有关量的计算
已知正三棱锥V ABC中,底面边长为8,侧棱长为,计算它的高和斜高.
思路分析:本题主要考查正三棱锥中基本量的计算,关键是把已知量与未知量放到直角三角形中求解.
解:如图所示,设O是底面中心,则D为BC的中点,
∴△VAO和△VCD都是直角三角形.
∵底面边长为8,侧棱长为2,
∴AO=×8=,CD=4,
∴VO===.
VD===2.
即正三棱锥的高是,斜高为2.
正三棱台的上、下底面边长分别为3和6,高为1,试求该棱台的侧棱和斜高.
解:如图,设上、下两底的中心分别是O1,O,连接O1O,则O1O为棱台的高,O1O=1.连接A1O1,AO并延长分别与B1C1和BC相交于D1,D.由平面几何知识得,D1,D分别是B1C1和BC的中点,连接D1D,则D1D为棱台的斜高.
因为B1C1=3,BC=6,所以A1O1=×3=,AO=×6=2,O1D1=×3=,OD=×6=.
在直角梯形AOO1A1中,A1A==2;
在直角梯形DOO1D1中,D1D==.
即该棱台的侧棱和斜高分别为2和.
正棱锥中基本量的计算要借助构造的直角三角形,如[活动与探究3]中的Rt△VAO,Rt△VOD,Rt△VCD等.它们包含了正棱锥的侧棱长、高、斜高、底面边长的一半,底面外接圆半径和内切圆半径.
类似地,在正棱台中,有三个重要的直角梯形——两底面中心连线、相应的边心距和斜高组成一个直角梯形;两底面中心连线、侧棱和相应两底面正多边形的顶点与中心连线组成一个直角梯形;斜高、侧棱和上下两底面边长的一半组成一个直角梯形.正棱台的计算问题,实际上就是这几个直角梯形的计算问题.
1.在棱柱中( ).
A.只有两个面平行
B.所有的棱都平行
C.所有的面都是平行四边形
D.两底面平行,且各侧棱也互相平行
答案:D
2.棱柱的侧面都是( ).
A.三角形
B.四边形
C.五边形
D.矩形
答案:B
3.从长方体的一个顶点出发的三条棱上各取一点E,F,G,过此三点作长方体的截面,那么截去的几何体是( ).
A.三棱柱
B.三棱锥
C.四棱柱
D.四棱锥
答案:B
4.下列描述中,是棱台的性质的是__________.(填序号)
①两底面平行;②侧面都是梯形;③侧棱都相等,且平行;④侧棱延长后都交于一点;⑤底面不可能为三角形.
解析:棱台是由棱锥截得的,截面与底面平行,①正确;棱台的侧面都是梯形,②正确;③错误;棱台侧棱延长后必交于一点,④正确;由三棱锥截得的棱台为三棱台,其底面是三角形,⑤错误.
答案:①②④
5.判断下列语句的对错.
(1)一个棱锥至少有四个面;
(2)如果四棱锥的底面是正方形,那么这个四棱锥的四条侧棱都相等;
(3)五棱锥只有五条棱;
(4)用与底面平行的平面去截三棱锥,得到的截面三角形和底面三角形相似.
解:(1)正确;
(2)不正确,四棱锥的底面是正方形,它的侧棱可以相等,也可以不相等;
(3)不正确,五棱锥除了五条侧棱外,还有五条底边,故共有10条棱;
(4)正确.
