1.3.2 由三视图还原实物图 学案1(含答案)
文档属性
| 名称 | 1.3.2 由三视图还原实物图 学案1(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 535.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-28 00:00:00 | ||
图片预览

文档简介
1.3.2 由三视图还原实物图 学案
1.理解三视图与直观图的联系与区别.
2.能根据三视图画出常见几何体及其组合体的实物图.
随着计算机技术的快速发展,三维打印技术越来越普及并且得到广泛的应用,其原理是:先通过计算机辅助设计(CAD)或计算机动画建模软件通过三个角度构造物体模型,在利用三维打印机将物体的模型打印出来.
问题1: 三维打印原理从数学角度上理解就是先设计 ,再还原 .?
由三视图还原为直观图的步骤:
问题2:由空间几何体的三视图还原直观图时,遵循的原则: , ,宽相等的基本原则,特别注意几何体中与投影面垂直或平行的线及面的关系.?
问题3:由常见几何体的三视图判断原物体的形状,一般规律如下表所示:
正(主)视图
侧(左)视图
俯视图
原几何体的形状
矩形
矩形
多边形
?
矩形
矩形
圆
?
三角形
三角形
多边形
?
三角形
三角形
圆(带圆心)
?
梯形
梯形
两个多边形
棱台
等腰梯形
等腰梯形
两个同心圆
圆台
特别注意,由正(主)视图和 的形状确定几何体是柱体、锥体或台体,由 确定几何体是多面体还是旋转体.?
问题4:根据三视图还原成实物图应注意:
(1)由三视图还原成实物图是由实物图画三视图的逆过程,在该过程中注意理解实物图画三视图的原理,并联想柱、锥、台、球体的三视图.
(2)由三视图还原成实物图时,一般以 为基础再结合 和 .?
(3)根据三视图还原实物图:需要综合正(主)视图、侧(左)视图、俯视图的特征,确定 ,找出组成几何体的简单几何体,再将组合还原,其中确定 是正确还原的关键.?
1.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是( ).
A.球 B.三棱锥 C.正方体 D.圆柱
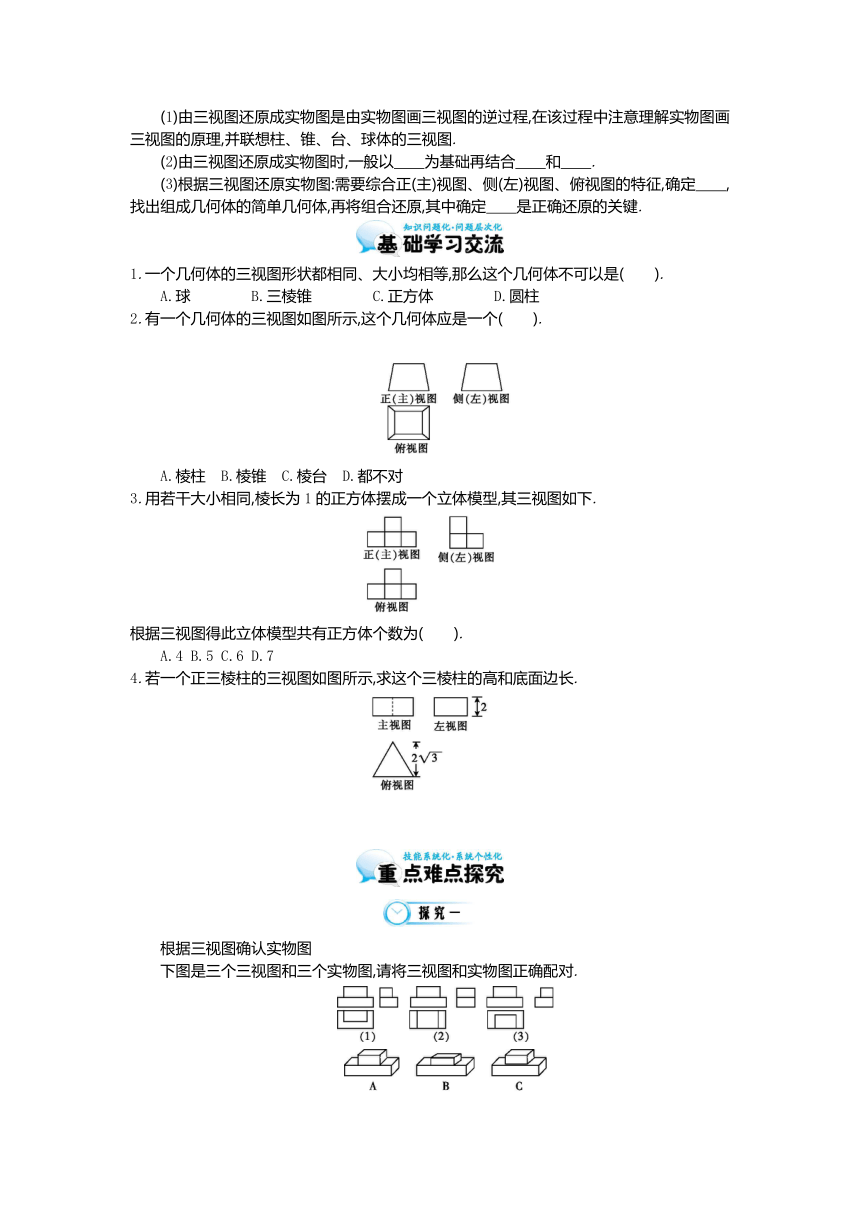
2.有一个几何体的三视图如图所示,这个几何体应是一个( ).
A.棱柱 B.棱锥 C.棱台 D.都不对
3.用若干大小相同,棱长为1的正方体摆成一个立体模型,其三视图如下.
根据三视图得此立体模型共有正方体个数为( ).
A.4 B.5 C.6 D.7
4.若一个正三棱柱的三视图如图所示,求这个三棱柱的高和底面边长.
根据三视图确认实物图
下图是三个三视图和三个实物图,请将三视图和实物图正确配对.
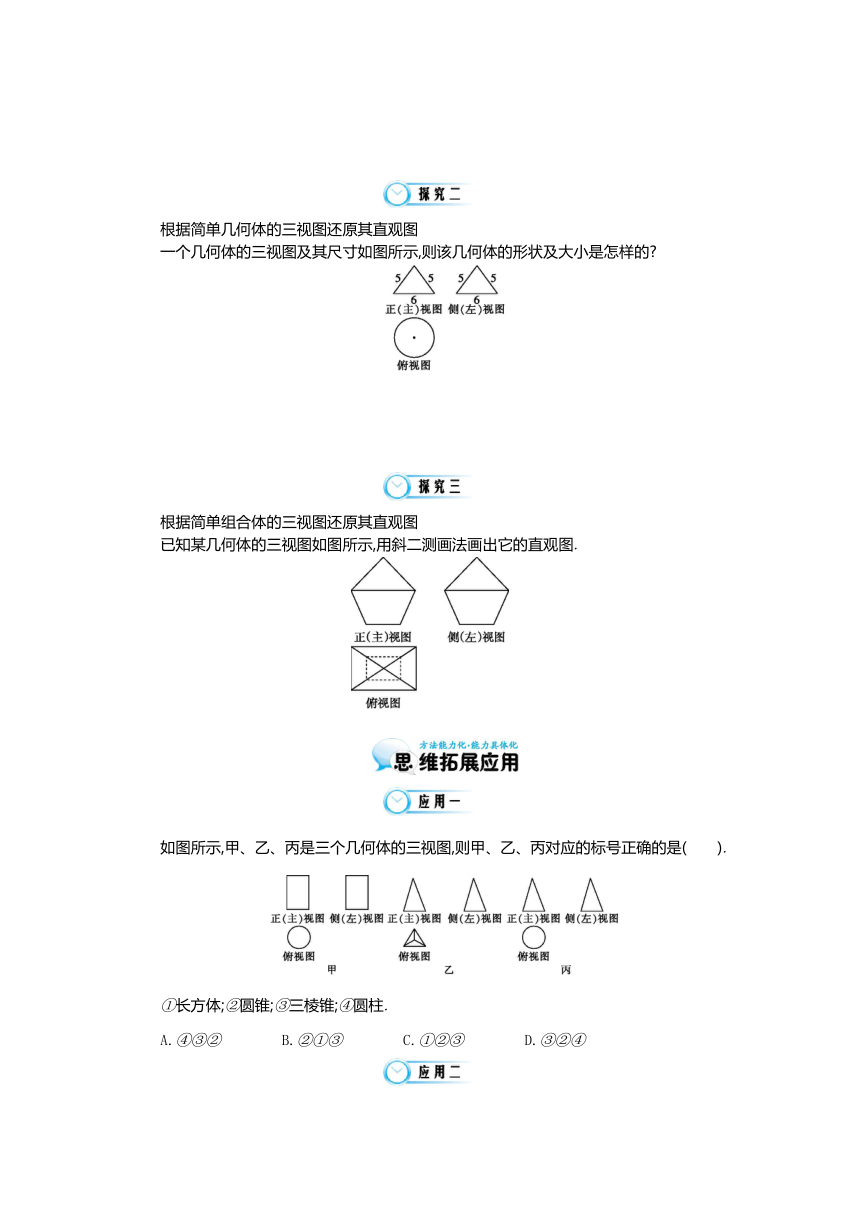
根据简单几何体的三视图还原其直观图
一个几何体的三视图及其尺寸如图所示,则该几何体的形状及大小是怎样的?
根据简单组合体的三视图还原其直观图
已知某几何体的三视图如图所示,用斜二测画法画出它的直观图.
如图所示,甲、乙、丙是三个几何体的三视图,则甲、乙、丙对应的标号正确的是( ).
①长方体;②圆锥;③三棱锥;④圆柱.
A.④③② B.②①③ C.①②③ D.③②④
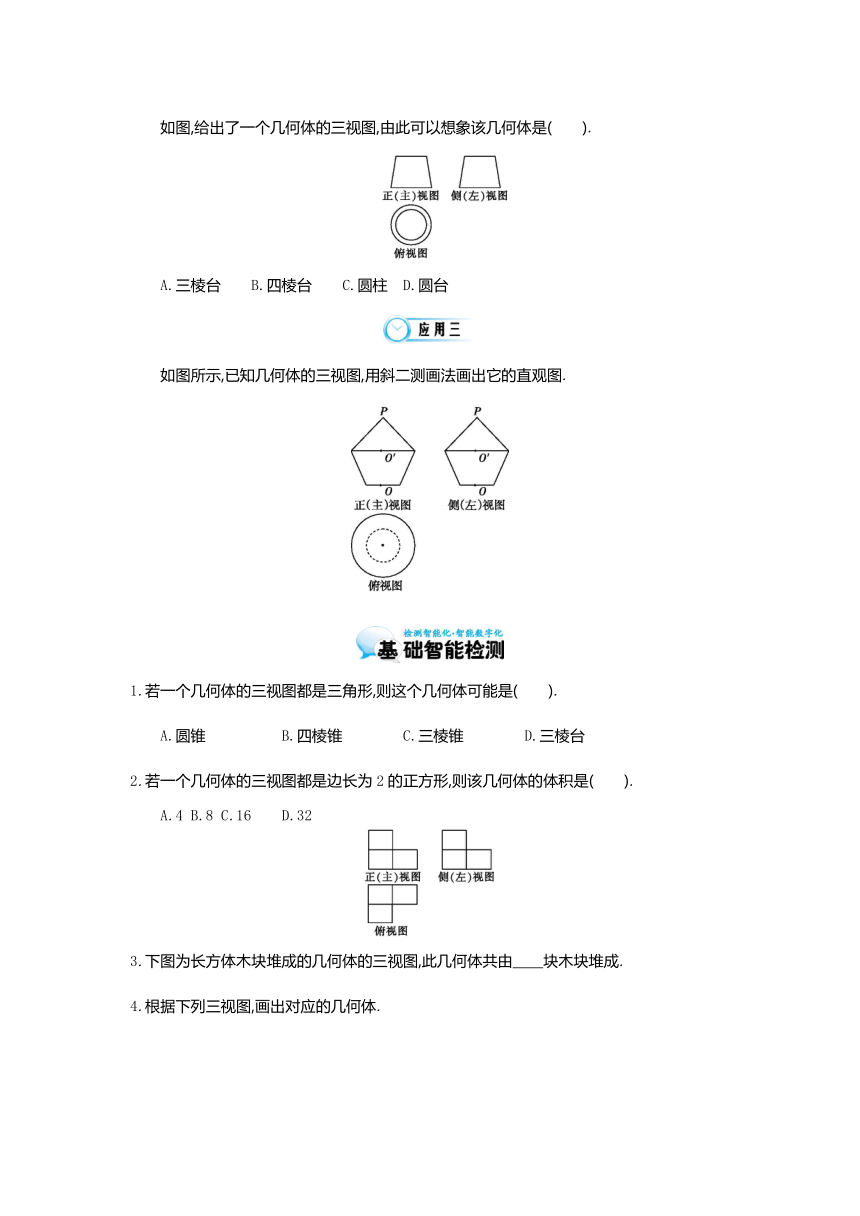
如图,给出了一个几何体的三视图,由此可以想象该几何体是( ).
A.三棱台 B.四棱台 C.圆柱 D.圆台
如图所示,已知几何体的三视图,用斜二测画法画出它的直观图.
1.若一个几何体的三视图都是三角形,则这个几何体可能是( ).
A.圆锥 B.四棱锥 C.三棱锥 D.三棱台
2.若一个几何体的三视图都是边长为2的正方形,则该几何体的体积是( ).
A.4 B.8 C.16 D.32
3.下图为长方体木块堆成的几何体的三视图,此几何体共由 块木块堆成.?
4.根据下列三视图,画出对应的几何体.
(2011年·浙江卷)若某几何体的三视图如图所示,则这个几何体的直观图可能是( ).
考题变式(我来改编):
第4课时 由三视图还原实物图
知识体系梳理
问题1:三视图 实物图
问题2:长对正 高平齐
问题3:棱柱 圆柱 棱锥 圆锥 侧(左)视图 俯视图
问题4:(2)俯视图 正(主)视图 侧(左)视图 (3)分界线 分界线
基础学习交流
1.D 圆柱的正(主)视图与侧(左)视图都是矩形,俯视图为圆.
2.C
3.B 由题意得可知正方体共5块.
4.解:由三视图可知,左视图中2为正三棱柱的高,俯视图中2为底面正三角形的高,所以正三棱柱的底面边长为2÷=4,即这个正三棱柱的高是2,底面边长是4.
重点难点探究
探究一:【解析】(1)的实物图是C;(2)的实物图是A;(3)的实物图是B.
【小结】解决三视图和实物图的配对问题,关键在于观察每个视图与实物的关系:正(主)视图反映了物体的上、下和左、右的特征,俯视图反映了物体的前、后和左、右的特征,侧(左)视图反映了物体的前、后和上、下的特征.
探究二:
【解析】由正(主)视图与侧(左)视图是全等的等腰三角形,俯视图为带圆心的圆,可知该几何体是圆锥,由正(主)视图可以知道圆锥的底面圆直径为6,母线长为5,从而可知圆锥的半径为3,高为4.其直观图如图所示.
【小结】由几何体的三视图还原为直观图时,一要注意抓住三视图的核心特征;二要注意将三视图与常见几何体的三视图进行比对、联系,这样一般常见几何体的直观图可以顺利得以还原.
探究三:【解析】(1)画轴.如图画x轴、y轴、z轴,使∠xOy=45°,∠xOz=90°.
(2)画底面.利用斜二测画法画出底面ABCD,在z轴上截取一点O',使OO'等于三视图中相应的高度,过O'作Ox的平行线O'x',Oy的平行线O'y',利用O'x'与O'y'画出面A'B'C'D'.
(3)画四棱锥的顶点.在Oz上取点P,使PO'等于三视图中相应的高.
(4)成图.连接PA',PB',PC',PD',AA',B'B,C'C,D'D,并擦去辅助线,即得到题中三视图所表示的几何体的直观图.
【小结】解决本类问题首先要根据三视图正确得出几何体的结构,几何体的结构不清易导致错误.
思维拓展应用
应用一:A 根据三视图可知,甲表示圆柱,乙表示三棱锥,丙表示圆锥,故选A.
应用二:D
应用三:由几何体的三视图可知,这个几何体是一个简单组合体,它的下部是一个圆台,上部是一个圆锥,并且圆锥的底面与圆台的上底面重合.画直观图时,我们可以先画出下部的圆台,再画出上部的圆锥.
画法: (1)画轴.如图①,画x轴、y轴、z轴,使∠xOy=45°.
(2)画圆台的两底面.利用斜二测画法,画出底面圆O,在z轴上截取OO',使OO'等于三视图中相应的高度,过O'作Ox的平行线O'x',Oy的平行线O'y',利用O'x'与O'y'画出上底面圆O'(与画圆O一样).
(3)画圆锥的顶点.在Oz上截取点P,使PO'等于三视图中相应的高度.
(4)成图.连接PA',PB',A'A,B'B,整理得到三视图所表示的几何体的直观图,如图②.
基础智能检测
1.C
2.B 由题意知该几何体是棱长为2的正方体,其体积为8.
3.4 根据三视图可以知道,该几何体如图所示.从图中可以看出是由四块长方体木块堆成.
4.解:几何体如图所示.
全新视角拓展
D A中正(主)视图,俯视图不对,故A错;B中正(主)视图,侧(左)视图不对,故B错;C中侧(左)视图,俯视图不对,故C错,故选D.
1.理解三视图与直观图的联系与区别.
2.能根据三视图画出常见几何体及其组合体的实物图.
随着计算机技术的快速发展,三维打印技术越来越普及并且得到广泛的应用,其原理是:先通过计算机辅助设计(CAD)或计算机动画建模软件通过三个角度构造物体模型,在利用三维打印机将物体的模型打印出来.
问题1: 三维打印原理从数学角度上理解就是先设计 ,再还原 .?
由三视图还原为直观图的步骤:
问题2:由空间几何体的三视图还原直观图时,遵循的原则: , ,宽相等的基本原则,特别注意几何体中与投影面垂直或平行的线及面的关系.?
问题3:由常见几何体的三视图判断原物体的形状,一般规律如下表所示:
正(主)视图
侧(左)视图
俯视图
原几何体的形状
矩形
矩形
多边形
?
矩形
矩形
圆
?
三角形
三角形
多边形
?
三角形
三角形
圆(带圆心)
?
梯形
梯形
两个多边形
棱台
等腰梯形
等腰梯形
两个同心圆
圆台
特别注意,由正(主)视图和 的形状确定几何体是柱体、锥体或台体,由 确定几何体是多面体还是旋转体.?
问题4:根据三视图还原成实物图应注意:
(1)由三视图还原成实物图是由实物图画三视图的逆过程,在该过程中注意理解实物图画三视图的原理,并联想柱、锥、台、球体的三视图.
(2)由三视图还原成实物图时,一般以 为基础再结合 和 .?
(3)根据三视图还原实物图:需要综合正(主)视图、侧(左)视图、俯视图的特征,确定 ,找出组成几何体的简单几何体,再将组合还原,其中确定 是正确还原的关键.?
1.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是( ).
A.球 B.三棱锥 C.正方体 D.圆柱
2.有一个几何体的三视图如图所示,这个几何体应是一个( ).
A.棱柱 B.棱锥 C.棱台 D.都不对
3.用若干大小相同,棱长为1的正方体摆成一个立体模型,其三视图如下.
根据三视图得此立体模型共有正方体个数为( ).
A.4 B.5 C.6 D.7
4.若一个正三棱柱的三视图如图所示,求这个三棱柱的高和底面边长.
根据三视图确认实物图
下图是三个三视图和三个实物图,请将三视图和实物图正确配对.
根据简单几何体的三视图还原其直观图
一个几何体的三视图及其尺寸如图所示,则该几何体的形状及大小是怎样的?
根据简单组合体的三视图还原其直观图
已知某几何体的三视图如图所示,用斜二测画法画出它的直观图.
如图所示,甲、乙、丙是三个几何体的三视图,则甲、乙、丙对应的标号正确的是( ).
①长方体;②圆锥;③三棱锥;④圆柱.
A.④③② B.②①③ C.①②③ D.③②④
如图,给出了一个几何体的三视图,由此可以想象该几何体是( ).
A.三棱台 B.四棱台 C.圆柱 D.圆台
如图所示,已知几何体的三视图,用斜二测画法画出它的直观图.
1.若一个几何体的三视图都是三角形,则这个几何体可能是( ).
A.圆锥 B.四棱锥 C.三棱锥 D.三棱台
2.若一个几何体的三视图都是边长为2的正方形,则该几何体的体积是( ).
A.4 B.8 C.16 D.32
3.下图为长方体木块堆成的几何体的三视图,此几何体共由 块木块堆成.?
4.根据下列三视图,画出对应的几何体.
(2011年·浙江卷)若某几何体的三视图如图所示,则这个几何体的直观图可能是( ).
考题变式(我来改编):
第4课时 由三视图还原实物图
知识体系梳理
问题1:三视图 实物图
问题2:长对正 高平齐
问题3:棱柱 圆柱 棱锥 圆锥 侧(左)视图 俯视图
问题4:(2)俯视图 正(主)视图 侧(左)视图 (3)分界线 分界线
基础学习交流
1.D 圆柱的正(主)视图与侧(左)视图都是矩形,俯视图为圆.
2.C
3.B 由题意得可知正方体共5块.
4.解:由三视图可知,左视图中2为正三棱柱的高,俯视图中2为底面正三角形的高,所以正三棱柱的底面边长为2÷=4,即这个正三棱柱的高是2,底面边长是4.
重点难点探究
探究一:【解析】(1)的实物图是C;(2)的实物图是A;(3)的实物图是B.
【小结】解决三视图和实物图的配对问题,关键在于观察每个视图与实物的关系:正(主)视图反映了物体的上、下和左、右的特征,俯视图反映了物体的前、后和左、右的特征,侧(左)视图反映了物体的前、后和上、下的特征.
探究二:
【解析】由正(主)视图与侧(左)视图是全等的等腰三角形,俯视图为带圆心的圆,可知该几何体是圆锥,由正(主)视图可以知道圆锥的底面圆直径为6,母线长为5,从而可知圆锥的半径为3,高为4.其直观图如图所示.
【小结】由几何体的三视图还原为直观图时,一要注意抓住三视图的核心特征;二要注意将三视图与常见几何体的三视图进行比对、联系,这样一般常见几何体的直观图可以顺利得以还原.
探究三:【解析】(1)画轴.如图画x轴、y轴、z轴,使∠xOy=45°,∠xOz=90°.
(2)画底面.利用斜二测画法画出底面ABCD,在z轴上截取一点O',使OO'等于三视图中相应的高度,过O'作Ox的平行线O'x',Oy的平行线O'y',利用O'x'与O'y'画出面A'B'C'D'.
(3)画四棱锥的顶点.在Oz上取点P,使PO'等于三视图中相应的高.
(4)成图.连接PA',PB',PC',PD',AA',B'B,C'C,D'D,并擦去辅助线,即得到题中三视图所表示的几何体的直观图.
【小结】解决本类问题首先要根据三视图正确得出几何体的结构,几何体的结构不清易导致错误.
思维拓展应用
应用一:A 根据三视图可知,甲表示圆柱,乙表示三棱锥,丙表示圆锥,故选A.
应用二:D
应用三:由几何体的三视图可知,这个几何体是一个简单组合体,它的下部是一个圆台,上部是一个圆锥,并且圆锥的底面与圆台的上底面重合.画直观图时,我们可以先画出下部的圆台,再画出上部的圆锥.
画法: (1)画轴.如图①,画x轴、y轴、z轴,使∠xOy=45°.
(2)画圆台的两底面.利用斜二测画法,画出底面圆O,在z轴上截取OO',使OO'等于三视图中相应的高度,过O'作Ox的平行线O'x',Oy的平行线O'y',利用O'x'与O'y'画出上底面圆O'(与画圆O一样).
(3)画圆锥的顶点.在Oz上截取点P,使PO'等于三视图中相应的高度.
(4)成图.连接PA',PB',A'A,B'B,整理得到三视图所表示的几何体的直观图,如图②.
基础智能检测
1.C
2.B 由题意知该几何体是棱长为2的正方体,其体积为8.
3.4 根据三视图可以知道,该几何体如图所示.从图中可以看出是由四块长方体木块堆成.
4.解:几何体如图所示.
全新视角拓展
D A中正(主)视图,俯视图不对,故A错;B中正(主)视图,侧(左)视图不对,故B错;C中侧(左)视图,俯视图不对,故C错,故选D.
