数学湘教版必修1:集合的基本运算(第1课时)
文档属性
| 名称 | 数学湘教版必修1:集合的基本运算(第1课时) |

|
|
| 格式 | rar | ||
| 文件大小 | 30.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-11 00:00:00 | ||
图片预览



文档简介
课件11张PPT。1.1.3 集合的基本运算第一课时一 学习目标理解两个集合的并集与交集的含义会求两个简单集合的并集与交集.
能使用Venn图表达集合的关系和运算体会直观图示对理解抽象概念的作用.
能够正确的理解不同语言表示的集合的本质并且能够在解题时准确表达.二 知识铺垫 我们知道,实数有加法运算.类比实数的加法运算,集合是否也可以“相加”呢?
考察下列各个集合,你能说出集合C与集合A、B之间的关系吗?
A={1,3,5},B={2,4,6},C={1,2,3,4,5,6};
A={x|x是有理数},B={x|x是无理数},C={x|x是实数}.
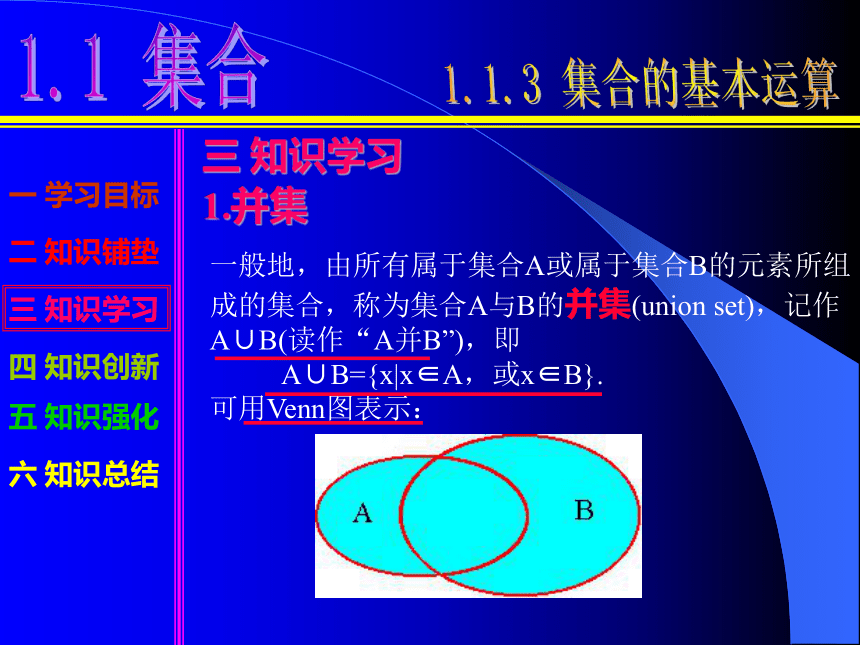
A={2,4,6,8,10},B={3,5,8,12},C={8}.三 知识学习1.并集一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集(union set),记作A∪B(读作“A并B”),即
A∪B={x|x∈A,或x∈B}.
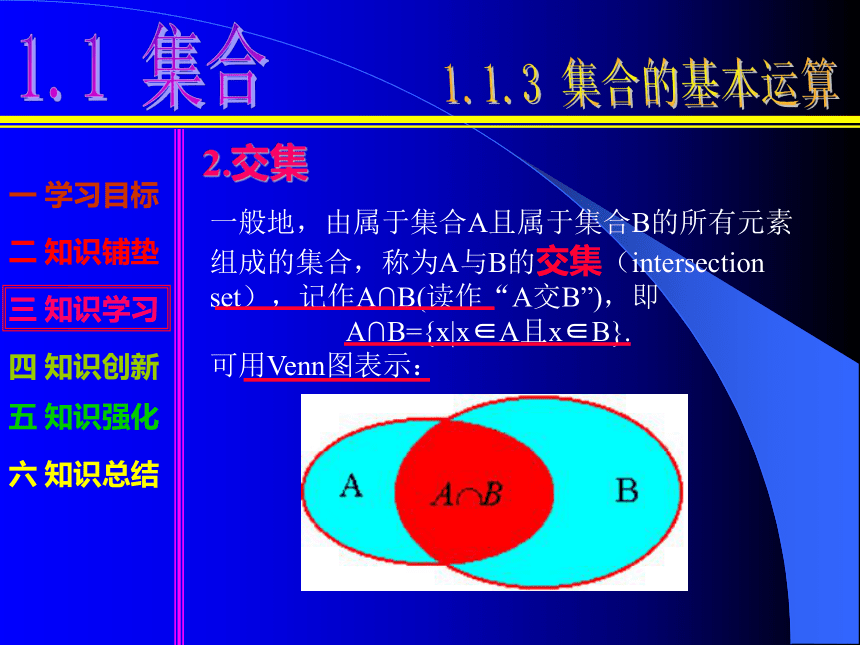
可用Venn图表示:2.交集一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集(intersection set),记作A∩B(读作“A交B”),即
A∩B={x|x∈A且x∈B}.
可用Venn图表示:四 知识创新根据右图讨论一下并集的运算性质四 知识创新根据右图讨论一下交集的运算性质五 知识强化练习1 已知A={x|x是等腰三角形},B={x|x是直角三 角形},求A∩B,A∪B. 答: A∩B ={x|x是等腰直角三角形}, A∪B ={x|x是等腰三角形或是直角三角形}练习2 A={x|x2-4x-5=0},B={x|x2=1},求A∩B, A∪B. 答: A∩B ={-1}, A∪B ={-1,1,5}练习3 已知集合A={x|x2-ax+a2-19=0}, B={x|x2-5x+6=0},C={x|x2+2x-8=0},求 a取何值时,A∩B≠ 与A∩C= 同 时成立.解:六 知识总结 本节我们学习了集合的并、交两种基本运算,要在理解其运算本质的基础上记忆其运算性质;在掌握概念的基础上能够熟练运用自然语言、符号语言、图形语言来表示集合的交、并运算.作业:课本第13页第6题.
能使用Venn图表达集合的关系和运算体会直观图示对理解抽象概念的作用.
能够正确的理解不同语言表示的集合的本质并且能够在解题时准确表达.二 知识铺垫 我们知道,实数有加法运算.类比实数的加法运算,集合是否也可以“相加”呢?
考察下列各个集合,你能说出集合C与集合A、B之间的关系吗?
A={1,3,5},B={2,4,6},C={1,2,3,4,5,6};
A={x|x是有理数},B={x|x是无理数},C={x|x是实数}.
A={2,4,6,8,10},B={3,5,8,12},C={8}.三 知识学习1.并集一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集(union set),记作A∪B(读作“A并B”),即
A∪B={x|x∈A,或x∈B}.
可用Venn图表示:2.交集一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集(intersection set),记作A∩B(读作“A交B”),即
A∩B={x|x∈A且x∈B}.
可用Venn图表示:四 知识创新根据右图讨论一下并集的运算性质四 知识创新根据右图讨论一下交集的运算性质五 知识强化练习1 已知A={x|x是等腰三角形},B={x|x是直角三 角形},求A∩B,A∪B. 答: A∩B ={x|x是等腰直角三角形}, A∪B ={x|x是等腰三角形或是直角三角形}练习2 A={x|x2-4x-5=0},B={x|x2=1},求A∩B, A∪B. 答: A∩B ={-1}, A∪B ={-1,1,5}练习3 已知集合A={x|x2-ax+a2-19=0}, B={x|x2-5x+6=0},C={x|x2+2x-8=0},求 a取何值时,A∩B≠ 与A∩C= 同 时成立.解:六 知识总结 本节我们学习了集合的并、交两种基本运算,要在理解其运算本质的基础上记忆其运算性质;在掌握概念的基础上能够熟练运用自然语言、符号语言、图形语言来表示集合的交、并运算.作业:课本第13页第6题.
