探究二力平衡的条件 课件 (4)
图片预览






文档简介
(共29张PPT)
沪科版新教材同步教学课件
第十章 机械与人
一 科学探究:杠杆平衡条件
一、杠杆模型
利用图中相关工具拔出板上的钉子。
【活动】
【思考】
1、这些工具自身都具有哪些共同特点?
2、在起钉子的过程中都还有哪些共性?
(有一定长度,外形各异,但整体受力不易形变的硬棒)
(绕点转动)
一、杠杆模型
在力的作用下可绕固定点转动的硬棒。
【杠杆】
【模型】
一些生活中可看作杠杆模型的工具。
【列举】
可见,杠杆不是特指某一种机械,而是满足
以上特征的各种机械的共同指称。
思考:杠杆的使用效果与哪些因素有关呢?
【思考】
一、杠杆模型
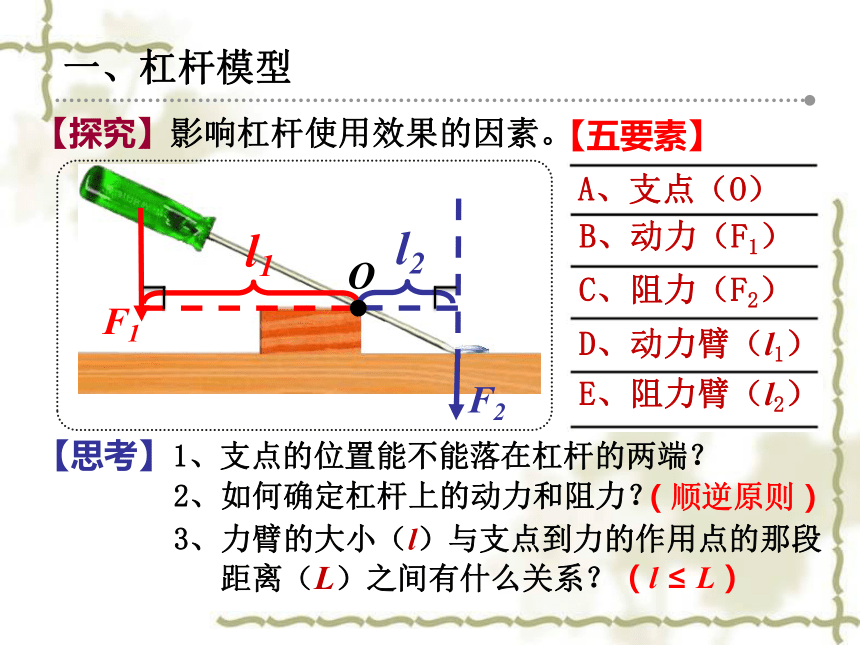
影响杠杆使用效果的因素。
【探究】
A、支点(O)
B、动力(F1)
C、阻力(F2)
D、动力臂(l1)
E、阻力臂(l2)
【五要素】
1、支点的位置能不能落在杠杆的两端?
2、如何确定杠杆上的动力和阻力?
3、力臂的大小(l)与支点到力的作用点的那段
距离(L)之间有什么关系?
(l ≤ L)
(顺逆原则)
l1
l2
O
F1
F2
例、如图所示的杠杆中,
O是 ,
若设F1是动力,则
F2是 ,
动力臂是 ,
阻力臂是 。
例、在下图杠杆中,画出对应的力或力臂。
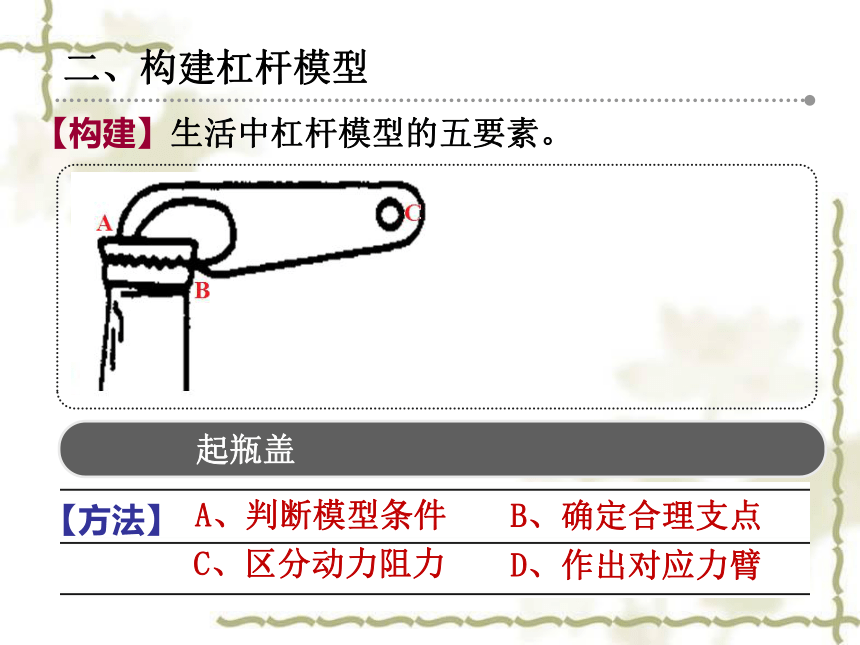
二、构建杠杆模型
生活中杠杆模型的五要素。
【构建】
起瓶盖
【方法】
A、判断模型条件
B、确定合理支点
C、区分动力阻力
D、作出对应力臂
二、构建杠杆模型
生活中的杠杆模型。
【体验】
组合类
变形类
直观类
二、构建杠杆模型
【钓鱼杆】
作出其杠杆模型的五要素。
二、构建杠杆模型
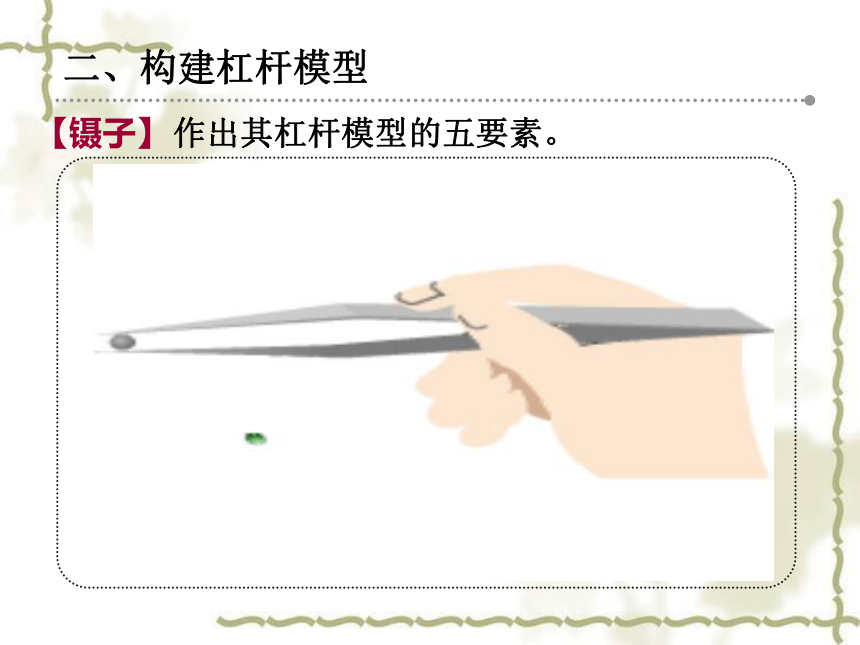
【镊子】
作出其杠杆模型的五要素。
二、构建杠杆模型
【人体关节】
作出手腕部杠杆模型的五要素。
例、构建下列杠杆模型,画出对应的五要素。
三、杠杆的平衡
静止或缓慢的匀速圆周转动。
【平衡状态】
【活动】
杠杆满足什么条件才能处于平衡状态呢?
力大则对应力臂要小,力小则对应力臂要大
体重不同的两人能不能让跷跷板稳定下来?
【思考】
【猜想】
评估
方案
结论
C.实验中如何快速测得动(阻)力臂?
(多个钩码)
四、探究杠杆平衡的条件
B.实验中如何方便地提供动力和阻力?
(平衡螺母)
这个探究实验给了我们哪些启示?
动力×动力臂=阻力×阻力臂
A.实验中如何解决杠杆自重对平衡的影响?
(水平位置平衡)
(弹簧测力计)
(刻度尺)
(在杠杆上标记均匀刻度)
四、探究杠杆平衡的条件
【实验过程】
【结论】
2、动力=阻力 动力臂=阻力臂
1、动力×动力臂=阻力×阻力臂
3、动力+动力臂=阻力+阻力臂
归纳总结实验结论。
四、探究杠杆平衡的条件
【实验评估】
1. 为什么要调节杠杆在水平位置平衡?
2. 为什么要进行多次实验探究?
(消除杠杆自重的影响)
(便于测量相应的力臂)
(便于从实验数据中归纳总结出可靠的一般规律)
【内容】
【公式】
【拓展】
【思考】
五、杠杆平衡原理
动力乘以动力臂等于阻力乘以阻力臂
F1l1=F2l2
杠杆受多个动(阻)力的平衡条件是什么呢?
给我一个支点和一根足够长的硬
棒,我就能撬动地球。
——阿基米德
F1l1+ Fnln =F2l2 + Fmlm
F1l1= F2l2
阿基米德撬地球的杠杆应该有什么特点呢?
1
省力杠杆
省力杠杆有哪些特点?
六、杠杆原理的应用
【杠杆的分类】
【特点】
动力臂大于阻力臂
动力小于阻力,省力
费距离
【实例】
起子
羊角锤
压水井手柄等
2
费力杠杆
六、杠杆原理的应用
【杠杆的分类】
【特点】
动力臂小于阻力臂
动力大于阻力,费力
省距离
【实例】
船桨等
笤帚
筷子
费力杠杆有哪些特点?
镊子
3
等臂杠杆
天平如果不等臂怎么修正?
六、杠杆原理的应用
【杠杆的分类】
【特点】
动力臂等于阻力臂
动力等于阻力,
不费力不省距离
【实例】
天平等
(等量替代)
六、杠杆原理的应用
【杆秤原理的研究】
【原理】
1、杆秤上的刻度线是否均匀分布?
3、有一种双提钮杆秤,双提钮的作用是什么?
2、长期使用秤砣生锈对测量结果有什么影响?
F1l1=F2l2
m物gAO=m砣gOB
m物=m砣OB/AO
m物与OB成正比
【思考】
(均匀)
(偏小)
(量程)
六、杠杆原理的应用
【平衡要素的计算】
【方法】
1、合理构建模型,明确平衡要素
3、注意单位统一,规范解题过程
2、对应杠杆原理,落实公式变形
六、杠杆原理的应用
【平衡要素的计算】
例、扁担长2m,两端物体的质量
分别为50kg和30kg。若不考虑扁
担的重力。人的肩头应在什么位
置,扁担才平衡
【解】
F1l1=F2l2
m1gAO=m2g(AB-AO)
50kgAO=30kg(2m-AO)
解之得:AO=0.75m
肩头离A端0.75m处,扁担可保持平衡。
【答】
六、杠杆原理的应用
例、如图,质量可忽略的杠杆上所标的每一格长度都是相
等的,0为支点,杠杆两边所挂的每一个钩码均相同,
杠杆在水平位置平衡。在下列情况下,杠杆仍在水平
位置保持平衡的是( )
A.两边都减少一个钩码
B.两边的钩码下各加挂一个
相同的钩码
C.左边钩码向右移一格,右
边钩码同时向左移一格
D.右边加挂一个相同钩码,左边钩码同时向左移一格
F1l1=F2l2
F1l1= F2l2
【动态平衡的分析】
六、杠杆原理的应用
【动态平衡的分析】
例、如图所示,一个轻质杠杆可绕轴O转动,在直杆
的中点挂一重物,在杆的另一端施加一个动力F,
将直杆从右下位置慢慢抬起到水平位置过程中,
力F大小的变化情况是 ( )
A.一直增大 B.一直减小
C.保持不变 D.无法确定
六、杠杆原理的应用
【动态平衡的分析】
例、如图所示,在一个轻质杠杆
的中点挂一重物,在杆的另
一端施加一个动力F,使杠
杆保持平衡,然后向右转动
F至水平方向,这一过程中
F变化情况是 ( )
A.一直增大 B.一直减小
C.先变小后变大 D.先变大后变小
思考:如何确定出使杠杆平衡的最小动力呢?
六、杠杆原理的应用
【最小动力的确定】
【方法】
1、合理确定支点O和动力作用点
3、作动力作用线,判断阻力作用效果
2、连线支点和动力作用点为最大动力臂
4、根据“顺逆原则”确定动力方向
六、杠杆原理的应用
【最小动力的确定】
可见,杠杆这一简单机械依然具有重要的价值
思考:怎么克服杠杆的这些缺陷呢?
七、杠杆的设计和选择
设计一个杠杆帮助人们从井中打水。
【活动】
沪科版新教材同步教学课件
第十章 机械与人
一 科学探究:杠杆平衡条件
一、杠杆模型
利用图中相关工具拔出板上的钉子。
【活动】
【思考】
1、这些工具自身都具有哪些共同特点?
2、在起钉子的过程中都还有哪些共性?
(有一定长度,外形各异,但整体受力不易形变的硬棒)
(绕点转动)
一、杠杆模型
在力的作用下可绕固定点转动的硬棒。
【杠杆】
【模型】
一些生活中可看作杠杆模型的工具。
【列举】
可见,杠杆不是特指某一种机械,而是满足
以上特征的各种机械的共同指称。
思考:杠杆的使用效果与哪些因素有关呢?
【思考】
一、杠杆模型
影响杠杆使用效果的因素。
【探究】
A、支点(O)
B、动力(F1)
C、阻力(F2)
D、动力臂(l1)
E、阻力臂(l2)
【五要素】
1、支点的位置能不能落在杠杆的两端?
2、如何确定杠杆上的动力和阻力?
3、力臂的大小(l)与支点到力的作用点的那段
距离(L)之间有什么关系?
(l ≤ L)
(顺逆原则)
l1
l2
O
F1
F2
例、如图所示的杠杆中,
O是 ,
若设F1是动力,则
F2是 ,
动力臂是 ,
阻力臂是 。
例、在下图杠杆中,画出对应的力或力臂。
二、构建杠杆模型
生活中杠杆模型的五要素。
【构建】
起瓶盖
【方法】
A、判断模型条件
B、确定合理支点
C、区分动力阻力
D、作出对应力臂
二、构建杠杆模型
生活中的杠杆模型。
【体验】
组合类
变形类
直观类
二、构建杠杆模型
【钓鱼杆】
作出其杠杆模型的五要素。
二、构建杠杆模型
【镊子】
作出其杠杆模型的五要素。
二、构建杠杆模型
【人体关节】
作出手腕部杠杆模型的五要素。
例、构建下列杠杆模型,画出对应的五要素。
三、杠杆的平衡
静止或缓慢的匀速圆周转动。
【平衡状态】
【活动】
杠杆满足什么条件才能处于平衡状态呢?
力大则对应力臂要小,力小则对应力臂要大
体重不同的两人能不能让跷跷板稳定下来?
【思考】
【猜想】
评估
方案
结论
C.实验中如何快速测得动(阻)力臂?
(多个钩码)
四、探究杠杆平衡的条件
B.实验中如何方便地提供动力和阻力?
(平衡螺母)
这个探究实验给了我们哪些启示?
动力×动力臂=阻力×阻力臂
A.实验中如何解决杠杆自重对平衡的影响?
(水平位置平衡)
(弹簧测力计)
(刻度尺)
(在杠杆上标记均匀刻度)
四、探究杠杆平衡的条件
【实验过程】
【结论】
2、动力=阻力 动力臂=阻力臂
1、动力×动力臂=阻力×阻力臂
3、动力+动力臂=阻力+阻力臂
归纳总结实验结论。
四、探究杠杆平衡的条件
【实验评估】
1. 为什么要调节杠杆在水平位置平衡?
2. 为什么要进行多次实验探究?
(消除杠杆自重的影响)
(便于测量相应的力臂)
(便于从实验数据中归纳总结出可靠的一般规律)
【内容】
【公式】
【拓展】
【思考】
五、杠杆平衡原理
动力乘以动力臂等于阻力乘以阻力臂
F1l1=F2l2
杠杆受多个动(阻)力的平衡条件是什么呢?
给我一个支点和一根足够长的硬
棒,我就能撬动地球。
——阿基米德
F1l1+ Fnln =F2l2 + Fmlm
F1l1= F2l2
阿基米德撬地球的杠杆应该有什么特点呢?
1
省力杠杆
省力杠杆有哪些特点?
六、杠杆原理的应用
【杠杆的分类】
【特点】
动力臂大于阻力臂
动力小于阻力,省力
费距离
【实例】
起子
羊角锤
压水井手柄等
2
费力杠杆
六、杠杆原理的应用
【杠杆的分类】
【特点】
动力臂小于阻力臂
动力大于阻力,费力
省距离
【实例】
船桨等
笤帚
筷子
费力杠杆有哪些特点?
镊子
3
等臂杠杆
天平如果不等臂怎么修正?
六、杠杆原理的应用
【杠杆的分类】
【特点】
动力臂等于阻力臂
动力等于阻力,
不费力不省距离
【实例】
天平等
(等量替代)
六、杠杆原理的应用
【杆秤原理的研究】
【原理】
1、杆秤上的刻度线是否均匀分布?
3、有一种双提钮杆秤,双提钮的作用是什么?
2、长期使用秤砣生锈对测量结果有什么影响?
F1l1=F2l2
m物gAO=m砣gOB
m物=m砣OB/AO
m物与OB成正比
【思考】
(均匀)
(偏小)
(量程)
六、杠杆原理的应用
【平衡要素的计算】
【方法】
1、合理构建模型,明确平衡要素
3、注意单位统一,规范解题过程
2、对应杠杆原理,落实公式变形
六、杠杆原理的应用
【平衡要素的计算】
例、扁担长2m,两端物体的质量
分别为50kg和30kg。若不考虑扁
担的重力。人的肩头应在什么位
置,扁担才平衡
【解】
F1l1=F2l2
m1gAO=m2g(AB-AO)
50kgAO=30kg(2m-AO)
解之得:AO=0.75m
肩头离A端0.75m处,扁担可保持平衡。
【答】
六、杠杆原理的应用
例、如图,质量可忽略的杠杆上所标的每一格长度都是相
等的,0为支点,杠杆两边所挂的每一个钩码均相同,
杠杆在水平位置平衡。在下列情况下,杠杆仍在水平
位置保持平衡的是( )
A.两边都减少一个钩码
B.两边的钩码下各加挂一个
相同的钩码
C.左边钩码向右移一格,右
边钩码同时向左移一格
D.右边加挂一个相同钩码,左边钩码同时向左移一格
F1l1=F2l2
F1l1= F2l2
【动态平衡的分析】
六、杠杆原理的应用
【动态平衡的分析】
例、如图所示,一个轻质杠杆可绕轴O转动,在直杆
的中点挂一重物,在杆的另一端施加一个动力F,
将直杆从右下位置慢慢抬起到水平位置过程中,
力F大小的变化情况是 ( )
A.一直增大 B.一直减小
C.保持不变 D.无法确定
六、杠杆原理的应用
【动态平衡的分析】
例、如图所示,在一个轻质杠杆
的中点挂一重物,在杆的另
一端施加一个动力F,使杠
杆保持平衡,然后向右转动
F至水平方向,这一过程中
F变化情况是 ( )
A.一直增大 B.一直减小
C.先变小后变大 D.先变大后变小
思考:如何确定出使杠杆平衡的最小动力呢?
六、杠杆原理的应用
【最小动力的确定】
【方法】
1、合理确定支点O和动力作用点
3、作动力作用线,判断阻力作用效果
2、连线支点和动力作用点为最大动力臂
4、根据“顺逆原则”确定动力方向
六、杠杆原理的应用
【最小动力的确定】
可见,杠杆这一简单机械依然具有重要的价值
思考:怎么克服杠杆的这些缺陷呢?
七、杠杆的设计和选择
设计一个杠杆帮助人们从井中打水。
【活动】
