湘教版数学必修一: 子集、全集、补集
图片预览








文档简介
课件22张PPT。子集、全集、补集问题:观察下列几组集合,它们之间的共同特点是什么?如何用符号描述这种关系?
(1)A={-1,1},B={-1,0,1};
(2)A=N,B=R;
(3)A={x│x是南京人},B={x│x是中国人}.
A 集合中的元素都是B 集合中的元素(A集合是B集合的一部分),
即:任意x∈A,则x∈B. 子 集(1)对于两个集合A和B,如果集合A的任何一个元素都是集合B的元素,则称集合A为集合B的子集.
记为:A?B (或B?A).
读作“集合A包含于集合B”
或“集合B包含集合A” .
(2)若任意x∈A ? x∈B,则A?B.思考:(1)A?A正确吗?
(2)A?B和B ?A能否同时成立?
(3)A?B和B ?A意味着什么?
(4)A?B,B ?C,你能得出什么结论?规定:
任何集合是它本身的子集,即A?A;
空集是任何集合的子集,即 ??A.A=BA ? CA?B,且B ?A
注意:区别“∈”和“?”的使用
(1) 元素与集合之间是属于关系,如
1∈N,-1?N;
(2)集合与集合之间是包含关系,如
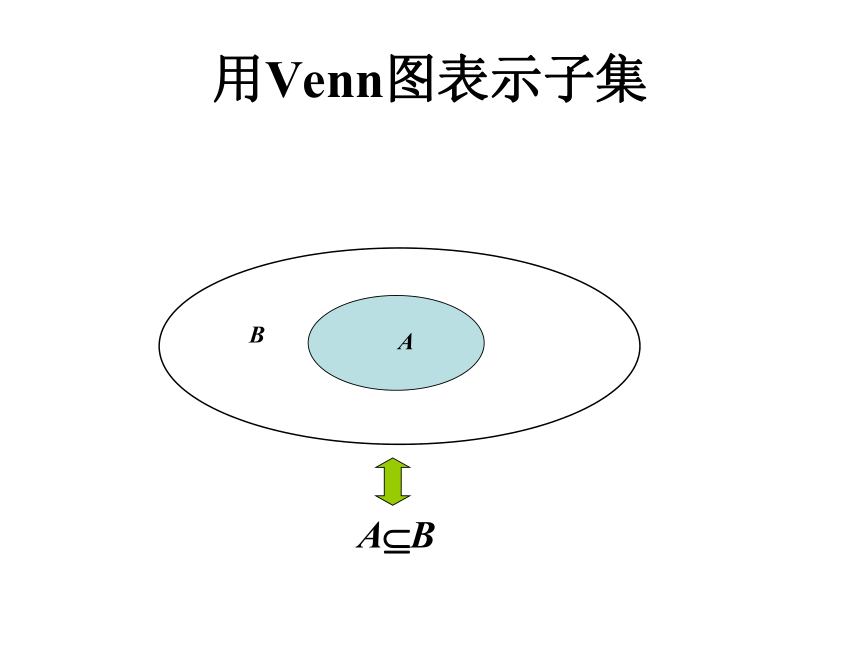
N?R,??R,{1}?{1,2,3}.用Venn图表示子集ABA?B例1:写出集合{a,b}的所有子集.
思考:
(1)如何书写有限集的所有子集?
(2)一个n元集合的子集个数有多少个?2n 个子集?,{a} , {b} ,{a,b}集合{a,b}的所有子集:
?,{a} , {b} ,{a,b}真子集(1)如果A?B ,并且A≠B ,则称集合A为集合B的真子集.
(2)记作:A?B 或 B?A.
(3)读作: “A真包含于B”或“B真包含A”.例2:用适当的符号填空:
(1)a_{a};
(2)a_{a,b,c};
(3)d_{a,b,c};
(4){a}_{a,b,c};
(5){a,b}_{b,a};
(6){3,5}_{1,3,5,7};
(7){2,4,6,8}_{2,8};
(8) ?_{1,2,3}例3:下列各组的三个集合中,哪两个集合之间具有包含关系?
(1)S={-2,-1,1,2},
A={-1,1},B={-2,2};
(2)S=R,A={x│x≤0,x∈R},
B={x│x>0,x∈R};
(3)S={x│x为地球人},A={x│x为中国人},B={x│x为外国人}.请观察上面集合A、B与集合S,它们之间有什么关系?用Venn图表示1,-1S x?B, x?S,且x?A(B)2,-2(A) 设A?S,由S中不属于A的所有元素组成的集合称为S的子集A的补集,
记作:?sA ={x|x?S,且x?A}.补 集全 集 如果集合S包含我们所要研究的各个集合的全部元素,这时将S看作是一个全集,通常记作:U.
例:在实数范围内讨论集合时,R可以看做一个全集U.
在实数范围内讨论问题时,可以把实数集看作全集U,那么,有理数集Q的补集
?s Q就是全体无理数的集合.
问题:设全集为U,A={1,2,3},根据下列条件求? U A:
(1)U={0,1,2,3,4,5};
(2)U={1,2,3,4}
(3)U={1,2,3}
几点说明(1)补集是相对全集而言,离开全集谈补集没有意义;
(2)若B= ? SA,则A=? SB,
即? S(?SA)=A;
(3) ? SS=?, ? S?=S.例1:不等式 的解集为A,
U=R,求A和 ? U A,将它们表示在数轴上.例2:已知集合S={1,2,3,4,5,6},A={1,3,5},试写出
? S A.例3:已知A={x|x<-1,或x>5},
B={x|a≤x<a+4},若A ? B,
求实数a的取值范围.≠例4:已知A={x| x2 +x-6=0},
B={x|ax+1 =0},若A ? B,
求实数a的取值范围.≠例5:设全集U={2,3,a2+2a-3},
A={b,2}, ? U A={5},求实数a、b的值.例6:设U=R,P={x|x≤1,或x≥3},
B={x|m≤x<m+1},
若所有满足B ? ? U P的m组成的集合为C,
求? U C.
(1)A={-1,1},B={-1,0,1};
(2)A=N,B=R;
(3)A={x│x是南京人},B={x│x是中国人}.
A 集合中的元素都是B 集合中的元素(A集合是B集合的一部分),
即:任意x∈A,则x∈B. 子 集(1)对于两个集合A和B,如果集合A的任何一个元素都是集合B的元素,则称集合A为集合B的子集.
记为:A?B (或B?A).
读作“集合A包含于集合B”
或“集合B包含集合A” .
(2)若任意x∈A ? x∈B,则A?B.思考:(1)A?A正确吗?
(2)A?B和B ?A能否同时成立?
(3)A?B和B ?A意味着什么?
(4)A?B,B ?C,你能得出什么结论?规定:
任何集合是它本身的子集,即A?A;
空集是任何集合的子集,即 ??A.A=BA ? CA?B,且B ?A
注意:区别“∈”和“?”的使用
(1) 元素与集合之间是属于关系,如
1∈N,-1?N;
(2)集合与集合之间是包含关系,如
N?R,??R,{1}?{1,2,3}.用Venn图表示子集ABA?B例1:写出集合{a,b}的所有子集.
思考:
(1)如何书写有限集的所有子集?
(2)一个n元集合的子集个数有多少个?2n 个子集?,{a} , {b} ,{a,b}集合{a,b}的所有子集:
?,{a} , {b} ,{a,b}真子集(1)如果A?B ,并且A≠B ,则称集合A为集合B的真子集.
(2)记作:A?B 或 B?A.
(3)读作: “A真包含于B”或“B真包含A”.例2:用适当的符号填空:
(1)a_{a};
(2)a_{a,b,c};
(3)d_{a,b,c};
(4){a}_{a,b,c};
(5){a,b}_{b,a};
(6){3,5}_{1,3,5,7};
(7){2,4,6,8}_{2,8};
(8) ?_{1,2,3}例3:下列各组的三个集合中,哪两个集合之间具有包含关系?
(1)S={-2,-1,1,2},
A={-1,1},B={-2,2};
(2)S=R,A={x│x≤0,x∈R},
B={x│x>0,x∈R};
(3)S={x│x为地球人},A={x│x为中国人},B={x│x为外国人}.请观察上面集合A、B与集合S,它们之间有什么关系?用Venn图表示1,-1S x?B, x?S,且x?A(B)2,-2(A) 设A?S,由S中不属于A的所有元素组成的集合称为S的子集A的补集,
记作:?sA ={x|x?S,且x?A}.补 集全 集 如果集合S包含我们所要研究的各个集合的全部元素,这时将S看作是一个全集,通常记作:U.
例:在实数范围内讨论集合时,R可以看做一个全集U.
在实数范围内讨论问题时,可以把实数集看作全集U,那么,有理数集Q的补集
?s Q就是全体无理数的集合.
问题:设全集为U,A={1,2,3},根据下列条件求? U A:
(1)U={0,1,2,3,4,5};
(2)U={1,2,3,4}
(3)U={1,2,3}
几点说明(1)补集是相对全集而言,离开全集谈补集没有意义;
(2)若B= ? SA,则A=? SB,
即? S(?SA)=A;
(3) ? SS=?, ? S?=S.例1:不等式 的解集为A,
U=R,求A和 ? U A,将它们表示在数轴上.例2:已知集合S={1,2,3,4,5,6},A={1,3,5},试写出
? S A.例3:已知A={x|x<-1,或x>5},
B={x|a≤x<a+4},若A ? B,
求实数a的取值范围.≠例4:已知A={x| x2 +x-6=0},
B={x|ax+1 =0},若A ? B,
求实数a的取值范围.≠例5:设全集U={2,3,a2+2a-3},
A={b,2}, ? U A={5},求实数a、b的值.例6:设U=R,P={x|x≤1,或x≥3},
B={x|m≤x<m+1},
若所有满足B ? ? U P的m组成的集合为C,
求? U C.
