等腰三角形课件
图片预览


文档简介
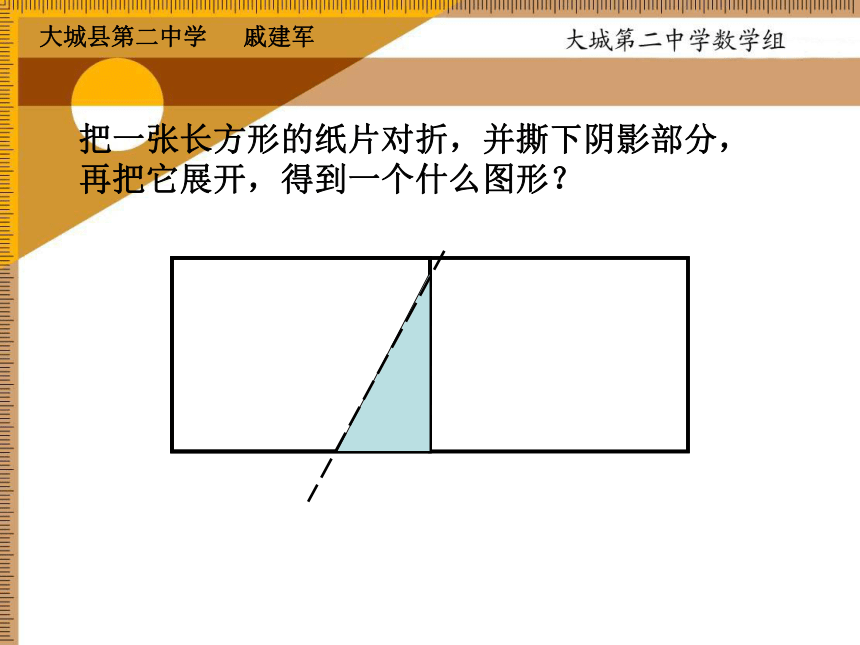
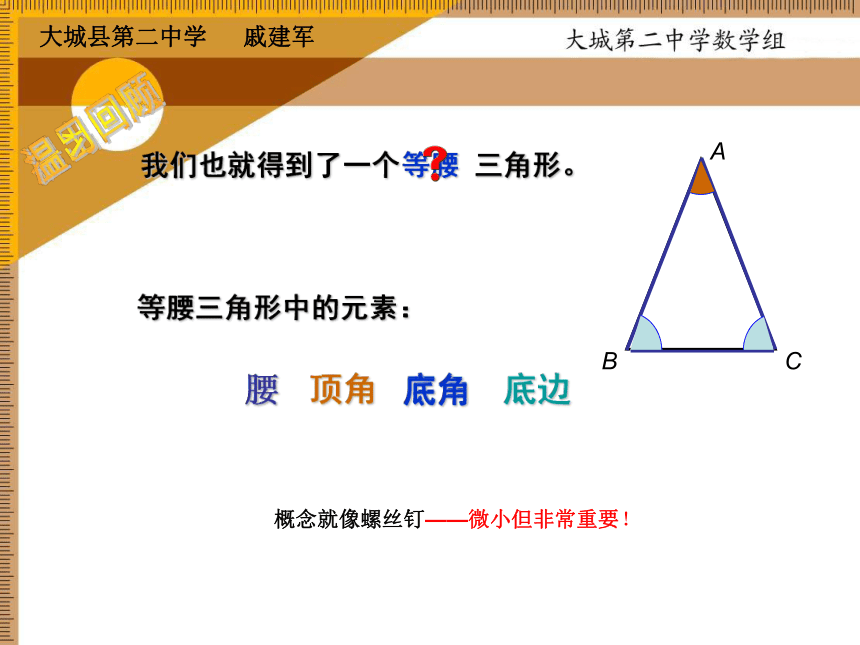
课件12张PPT。观察下列图片中的三角形的边有什么共同特点?发现问题等腰三角形把一张长方形的纸片对折,并撕下阴影部分,再把它展开,得到一个什么图形?概念就像螺丝钉——微小但非常重要!顶角底边腰腰底角底角我们也就得到了一个等腰等腰三角形中的元素:三角形。提出问题温习回顾你能把一个等腰三角形纸片折叠成完全重合的两部分吗?
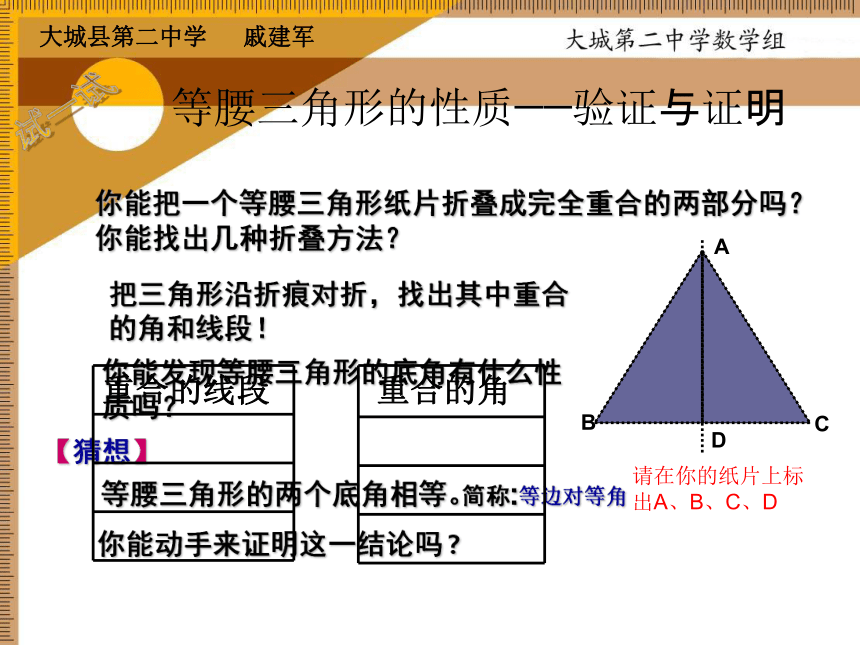
你能找出几种折叠方法?试一试你能发现等腰三角形的底角有什么性质吗?ABCD等腰三角形的两个底角相等。【猜想】等腰三角形的性质——验证与证明你能动手来证明这一结论吗?简称:等边对等角把三角形沿折痕对折,找出其中重合的角和线段!请在你的纸片上标
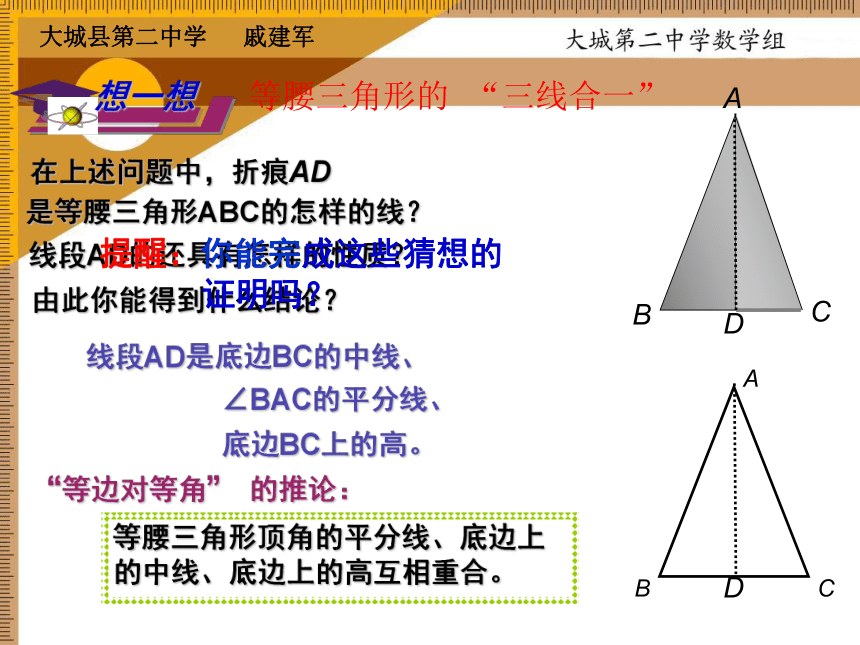
出A、B、C、D等腰三角形的 “三线合一”在上述问题中,折痕AD是等腰三角形ABC的怎样的线?线段AD的还具有怎样的性质?由此你能得到什么结论?等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合。 “等边对等角” 的推论:线段AD是底边BC的中线、∠BAC的平分线、底边BC上的高。提醒:你能完成这些猜想的
证明吗?如图△ABC中,AB=AC,求证:∠B=∠C。如何证明 ?把折好的纸打开不难发现折痕两旁的的两个三角形全等。由此实验得到启发——折痕就是
我们用于证明时要添加的辅助线。“等边对等角”——由实验到论证受性质1证明的启发,你能证明性质2(三线合一)吗?D提醒:
我们又多了一种证明角
相等、线段相等、线段
垂直的新的方法。例题 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。实践应用ABCD∵在△BDC中 BD=BC
∴∠BDC=∠C解: ∵在△ABC中 AB=AC
∴∠ABC=∠C∵在△ABD中 AD=BD
∴∠A=∠ABD
且∠A+∠ABD=∠BDC 又 ∵在△ABC中∠A+∠ABC+∠C=180° ∴∠A+2∠A+2∠A=180°即 2 ∠A= ∠BDC=∠C=∠ABC即∠A=36 ° ∴∠ABC=∠C=72°问题1 如果等腰三角形的顶角是36?,那么它的底角的度数是 。实践应用问题2 △ABC中,AB=AC,∠BAC=90?,AD是BC边上的高,则∠ABD= ,BD=______=______。ABCD变式练习 等腰三角形的一个角是 ,那么它的另外两个角的度数是 。36?110?72?、72?72?、72 ?或36?、108?35?、35?45°ADCD链接P 56习 题 12.3 你能整理它们吗小结作业第1、4、6题。 这节课我们主要学习了什么内容?有哪些收获?性质1:等腰三角形的两个底角相等;(简称“等边对等角”)
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。
(简称“三线合一”)
收获:
学完等腰三角形性质后,
我们又多了一种证明角
相等、线段相等、线段
垂直的新的方法。思考题思考 如图,在△ABC中,AB=AD=DC,
∠BAD=26°,求∠B和∠C的度数。BCDA返回小结答案思考 如图,在△ABC中,AB=AD=DC,
∠BAD=26°,求∠B和∠C的度数。返回小结解:∵△ABD中, AB=AD
∴∠ABD=∠ADB
又∵ ∠BAD=26°, ∠B+ ∠BAD+ ∠ADB=180°
∴∠B=∠ADB=(180 °-26 °) ÷2=77 °
在△ADC中, AD=DC
∴∠CAD=∠C
又∵ ∠ADB=∠CAD+∠C
即: 2∠C= 77 °
∴∠C=38.5 °
你能找出几种折叠方法?试一试你能发现等腰三角形的底角有什么性质吗?ABCD等腰三角形的两个底角相等。【猜想】等腰三角形的性质——验证与证明你能动手来证明这一结论吗?简称:等边对等角把三角形沿折痕对折,找出其中重合的角和线段!请在你的纸片上标
出A、B、C、D等腰三角形的 “三线合一”在上述问题中,折痕AD是等腰三角形ABC的怎样的线?线段AD的还具有怎样的性质?由此你能得到什么结论?等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合。 “等边对等角” 的推论:线段AD是底边BC的中线、∠BAC的平分线、底边BC上的高。提醒:你能完成这些猜想的
证明吗?如图△ABC中,AB=AC,求证:∠B=∠C。如何证明 ?把折好的纸打开不难发现折痕两旁的的两个三角形全等。由此实验得到启发——折痕就是
我们用于证明时要添加的辅助线。“等边对等角”——由实验到论证受性质1证明的启发,你能证明性质2(三线合一)吗?D提醒:
我们又多了一种证明角
相等、线段相等、线段
垂直的新的方法。例题 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。实践应用ABCD∵在△BDC中 BD=BC
∴∠BDC=∠C解: ∵在△ABC中 AB=AC
∴∠ABC=∠C∵在△ABD中 AD=BD
∴∠A=∠ABD
且∠A+∠ABD=∠BDC 又 ∵在△ABC中∠A+∠ABC+∠C=180° ∴∠A+2∠A+2∠A=180°即 2 ∠A= ∠BDC=∠C=∠ABC即∠A=36 ° ∴∠ABC=∠C=72°问题1 如果等腰三角形的顶角是36?,那么它的底角的度数是 。实践应用问题2 △ABC中,AB=AC,∠BAC=90?,AD是BC边上的高,则∠ABD= ,BD=______=______。ABCD变式练习 等腰三角形的一个角是 ,那么它的另外两个角的度数是 。36?110?72?、72?72?、72 ?或36?、108?35?、35?45°ADCD链接P 56习 题 12.3 你能整理它们吗小结作业第1、4、6题。 这节课我们主要学习了什么内容?有哪些收获?性质1:等腰三角形的两个底角相等;(简称“等边对等角”)
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。
(简称“三线合一”)
收获:
学完等腰三角形性质后,
我们又多了一种证明角
相等、线段相等、线段
垂直的新的方法。思考题思考 如图,在△ABC中,AB=AD=DC,
∠BAD=26°,求∠B和∠C的度数。BCDA返回小结答案思考 如图,在△ABC中,AB=AD=DC,
∠BAD=26°,求∠B和∠C的度数。返回小结解:∵△ABD中, AB=AD
∴∠ABD=∠ADB
又∵ ∠BAD=26°, ∠B+ ∠BAD+ ∠ADB=180°
∴∠B=∠ADB=(180 °-26 °) ÷2=77 °
在△ADC中, AD=DC
∴∠CAD=∠C
又∵ ∠ADB=∠CAD+∠C
即: 2∠C= 77 °
∴∠C=38.5 °
