多边形的内角和课件(22张PPT)
文档属性
| 名称 | 多边形的内角和课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 483.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-28 00:02:49 | ||
图片预览





文档简介
课件22张PPT。海拉尔第七中学吴国艳问题2:你知道长方形和正方形的内角和是多少吗?
其它四边形的内角和是多少?
问题1:你还记得三角形内角和是多少度?(三角形内角和 180°)(都是360°) 复习旧知 你会利用三角形的内角和计算四边形ABCD的内角和吗?请你与同学们交流你的证明思路. 连接对角线把四边形转化为两个三角形。 观察上图:可以看出四边形从一个顶点出发,
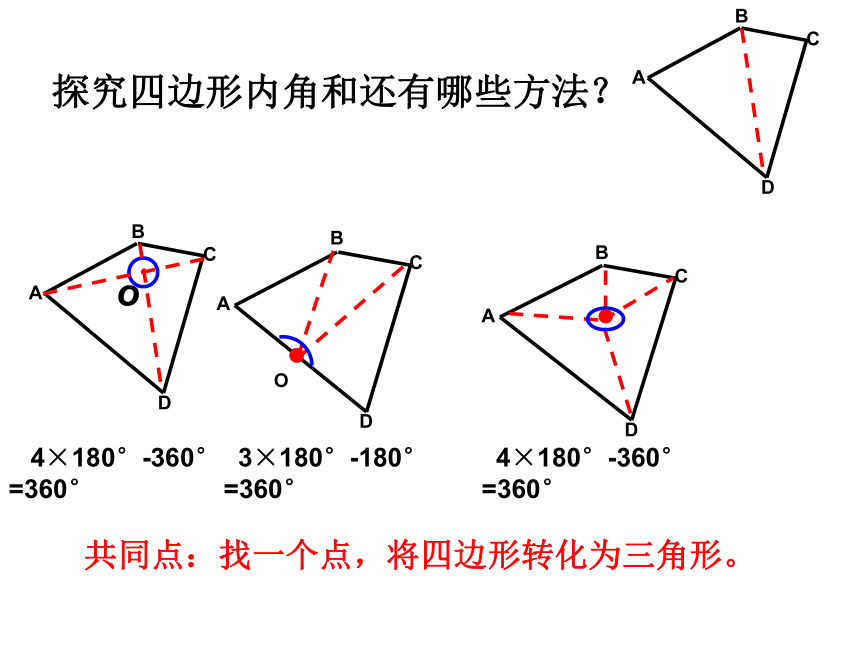
可以连___条对角线,它们将四边形分成_____ 个三角形,所以四边形的内角和为_____ 。1 2 360° 2×1800=3600 多边形内角和的探究探究四边形内角和还有哪些方法?O●● 4×180°-360° =360° 3×180°-180°
=360° 4×180°-360°
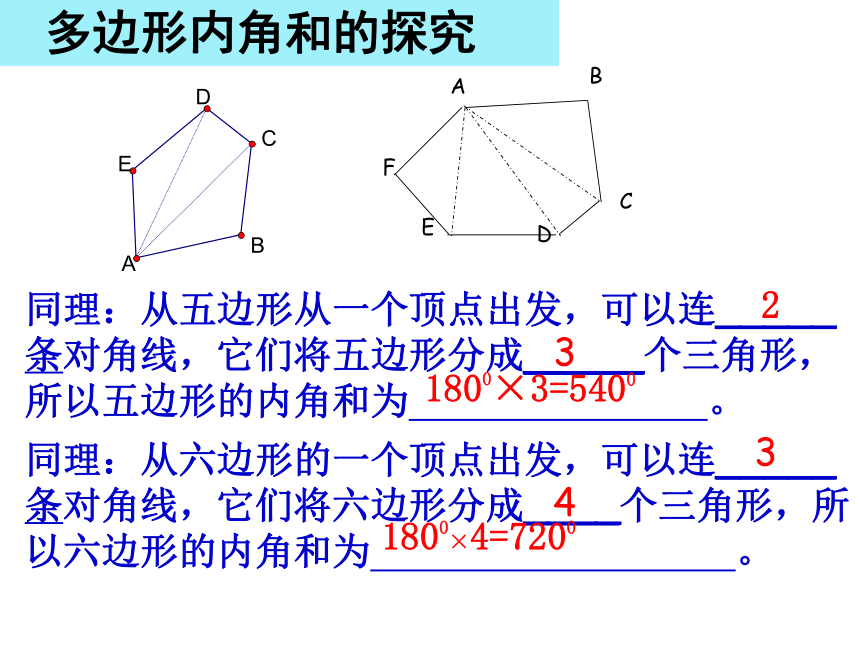
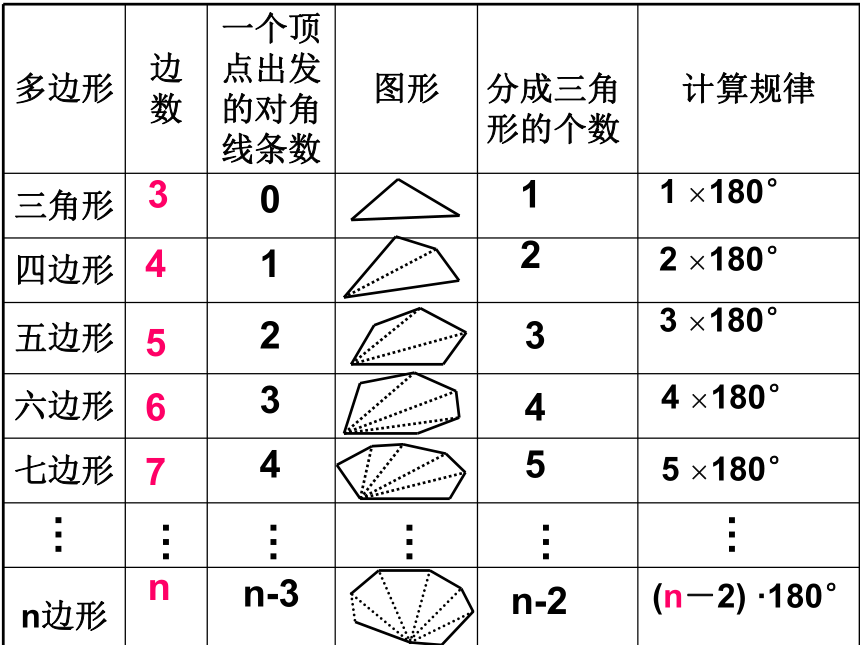
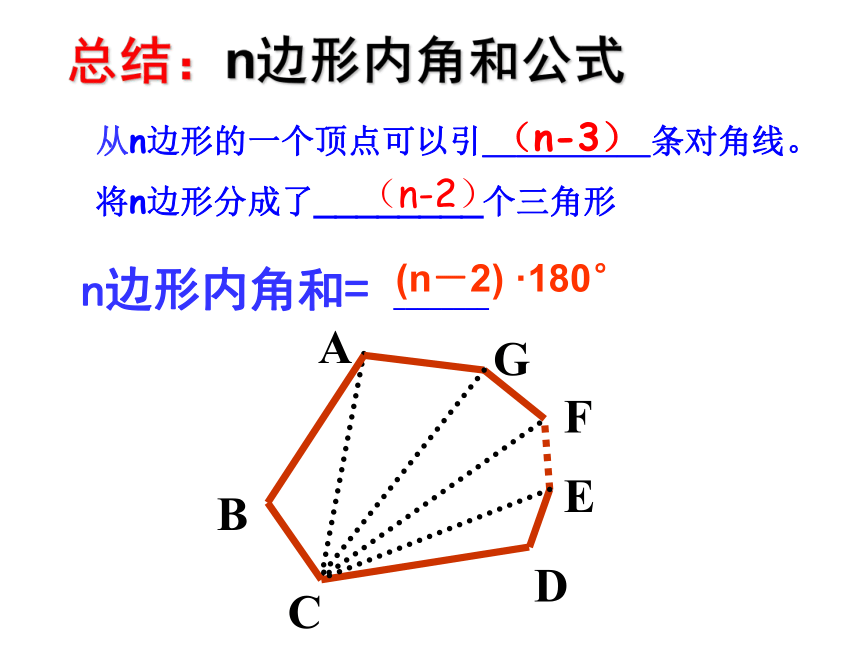
=360° 共同点:找一个点,将四边形转化为三角形。ABCDEF同理:从五边形从一个顶点出发,可以连_____条对角线,它们将五边形分成_____个三角形,所以五边形的内角和为 。2 3 同理:从六边形的一个顶点出发,可以连_____条对角线,它们将六边形分成____个三角形,所以六边形的内角和为 。3 4 1800×4=72001800×3=5400 多边形内角和的探究………………34567n0n-3123412345n-2(n-2) ·180°5 ×180°4 ×180°3 ×180°2 ×180°1 ×180°总结:n边形内角和公式n边形内角和= ________ 从n边形的一个顶点可以引_____条对角线。
将n边形分成了________个三角形
(n-3)(n-2)(n-2) ·180°(1)十二边形的内角和是多少?解:(12-2)×180°
=10 ×180°
=1800 °
答:十二边形的内角和为1800 °已知边数求多边形内角和 练习1.(2)一个多边形的内角和为2700°,求它的边数。解 :设这是一个n边形,根据题意得:
(n-2)·180 °=2700 °
n=17
答:它的边数为17.已知多边形内角和求边数例1.如果一个四边形的一组对角互补,那么另一组对角有什么关系?如果四边形一组对角互补,那么另一组对角也互补。
例题讲解变式:如图,OB⊥AB,垂足为B,OC⊥AC,垂足为C,试判断∠A与∠1有什么关系? 相等 例题变式 例2 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和 结论:五边形的外角和等于360°-(5-2) × 180°=360 ° 6=5个平角-5边形内角和=5×180° 例题讲解探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.n边形外角和=结论:
n边形的外角和等于360°-(n-2) × 180°=360 °n个平角-n边形内角和=n×180 ° (1)小明每从一条小路转到下一条小路时,身体转过的角是哪个角?
(2)猜想他每跑完一圈,身体转过的角度之和是多少?
♀ 清晨 ,小明沿一个五边形广场周围的小路按逆时针方向跑步。 (4)已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。 解: 设多边形的边数为n
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360o,
∴ (n-2)?180°=2× 360o。
解得: n=6
∴这个多边形的边数为6。
练习2. 回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?每个内角的度数是每个外角的度数是 正多边形一个正多边形的每一个内角都等于135°,则这个多边形是几边形?解法一:设这个多边形是n边形,由题意得
(n-2)×180o=n × 135o
解得:n=8
答:这个多边形是八边形。 解法二:由每个内角得135度可知每个外角得45度
又因为外角和得360度,可求边数为360÷ 45=8
答:这个多边形是八边形。 练习3小结通过本节课你有哪些收获1、若一个多边形的内角和等于1080°,则这个多边形的边数是_______。
2、七边形的内角和等于_______。
3、正五边形的每个内角是________。
4、下列角度中,不能成为多边形的内角和的是( )
(A)540° (B)580° (C)1800° (D)900°
5、从n边形的一个顶点出发画对角线,最多可以画_____条,这些对角线把n边形分成_____ 个三角形。8900°108°B(n-3)(n-2)⊿如图,求∠A+∠B+∠C+∠D+∠E+∠F的值。12
教出来的是知识,而
悟出来的是智慧。
作业:必做题 习题11.3 2、4、5
选做题 9、10
其它四边形的内角和是多少?
问题1:你还记得三角形内角和是多少度?(三角形内角和 180°)(都是360°) 复习旧知 你会利用三角形的内角和计算四边形ABCD的内角和吗?请你与同学们交流你的证明思路. 连接对角线把四边形转化为两个三角形。 观察上图:可以看出四边形从一个顶点出发,
可以连___条对角线,它们将四边形分成_____ 个三角形,所以四边形的内角和为_____ 。1 2 360° 2×1800=3600 多边形内角和的探究探究四边形内角和还有哪些方法?O●● 4×180°-360° =360° 3×180°-180°
=360° 4×180°-360°
=360° 共同点:找一个点,将四边形转化为三角形。ABCDEF同理:从五边形从一个顶点出发,可以连_____条对角线,它们将五边形分成_____个三角形,所以五边形的内角和为 。2 3 同理:从六边形的一个顶点出发,可以连_____条对角线,它们将六边形分成____个三角形,所以六边形的内角和为 。3 4 1800×4=72001800×3=5400 多边形内角和的探究………………34567n0n-3123412345n-2(n-2) ·180°5 ×180°4 ×180°3 ×180°2 ×180°1 ×180°总结:n边形内角和公式n边形内角和= ________ 从n边形的一个顶点可以引_____条对角线。
将n边形分成了________个三角形
(n-3)(n-2)(n-2) ·180°(1)十二边形的内角和是多少?解:(12-2)×180°
=10 ×180°
=1800 °
答:十二边形的内角和为1800 °已知边数求多边形内角和 练习1.(2)一个多边形的内角和为2700°,求它的边数。解 :设这是一个n边形,根据题意得:
(n-2)·180 °=2700 °
n=17
答:它的边数为17.已知多边形内角和求边数例1.如果一个四边形的一组对角互补,那么另一组对角有什么关系?如果四边形一组对角互补,那么另一组对角也互补。
例题讲解变式:如图,OB⊥AB,垂足为B,OC⊥AC,垂足为C,试判断∠A与∠1有什么关系? 相等 例题变式 例2 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和 结论:五边形的外角和等于360°-(5-2) × 180°=360 ° 6=5个平角-5边形内角和=5×180° 例题讲解探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.n边形外角和=结论:
n边形的外角和等于360°-(n-2) × 180°=360 °n个平角-n边形内角和=n×180 ° (1)小明每从一条小路转到下一条小路时,身体转过的角是哪个角?
(2)猜想他每跑完一圈,身体转过的角度之和是多少?
♀ 清晨 ,小明沿一个五边形广场周围的小路按逆时针方向跑步。 (4)已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。 解: 设多边形的边数为n
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360o,
∴ (n-2)?180°=2× 360o。
解得: n=6
∴这个多边形的边数为6。
练习2. 回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?每个内角的度数是每个外角的度数是 正多边形一个正多边形的每一个内角都等于135°,则这个多边形是几边形?解法一:设这个多边形是n边形,由题意得
(n-2)×180o=n × 135o
解得:n=8
答:这个多边形是八边形。 解法二:由每个内角得135度可知每个外角得45度
又因为外角和得360度,可求边数为360÷ 45=8
答:这个多边形是八边形。 练习3小结通过本节课你有哪些收获1、若一个多边形的内角和等于1080°,则这个多边形的边数是_______。
2、七边形的内角和等于_______。
3、正五边形的每个内角是________。
4、下列角度中,不能成为多边形的内角和的是( )
(A)540° (B)580° (C)1800° (D)900°
5、从n边形的一个顶点出发画对角线,最多可以画_____条,这些对角线把n边形分成_____ 个三角形。8900°108°B(n-3)(n-2)⊿如图,求∠A+∠B+∠C+∠D+∠E+∠F的值。12
教出来的是知识,而
悟出来的是智慧。
作业:必做题 习题11.3 2、4、5
选做题 9、10
