青岛版九年级数学上册第二单元复习题(含答案)
文档属性
| 名称 | 青岛版九年级数学上册第二单元复习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 159.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-28 00:00:00 | ||
图片预览

文档简介
青岛版九年级数学上册第二单元复习题(含答案)
一.选择题(共12小题)
1.如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于( )
A. B. C. D.
(1题图) (6题图) (7题图) (9题图)
2.在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,下列各式成立的是( )
A.b=a?sinB B.a=b?cosB C.a=b?tanB D.b=a?tanB
3.计算cos30°的值为( )
A. B. C.1 D.3
4.在△ABC中,(2cosA﹣)2+|1﹣tanB|=0,则△ABC一定是( )
A.直角三角形 B.等腰三角形
C.等边三角形 D.等腰直角三角形
5.在Rt△ABC中,∠C=90°,sinA=,AC=6cm,则BC的长度为( )
A.6cm B.7cm C.8cm D.9cm
6.如图,△ABC中,AC=5,cosB=,sinC=,则△ABC的面积为( )
A. B.12 C.14 D.21
7.如图,小颖利用一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是( )
A.4m B.m C.(5+)m D.(+)m
8.一辆汽车沿坡角为α的斜坡前进500米,则它上升的最大高度为( )
A.500sinα B. C.500cosα D.
9.如图,为了测量某建筑物MN的高度,在平地上A处测得建筑物顶端M的仰角为30°,向N点方向前进16m到达B处,在B处测得建筑物顶端M的仰角为45°,则建筑物MN的高度等于( )
A.8()m B.8()m C.16()m D.16()m
10.如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )
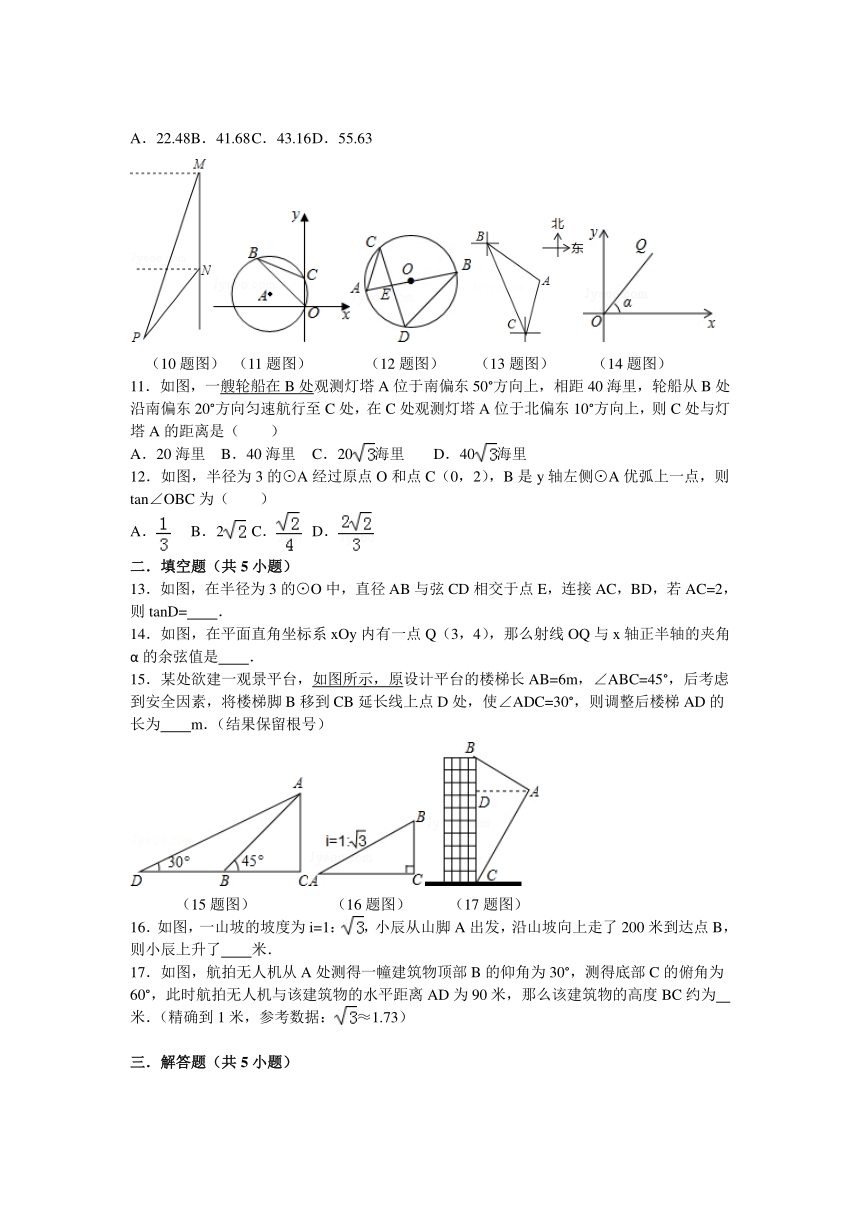
A.22.48 B.41.68 C.43.16 D.55.63
(10题图) (11题图) (12题图) (13题图) (14题图)
11.如图,一艘轮船在B处观测灯塔A位于南偏东50°方向上,相距40海里,轮船从B处沿南偏东20°方向匀速航行至C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
A.20海里 B.40海里 C.20海里 D.40海里
12.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A. B.2 C. D.
二.填空题(共5小题)
13.如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD= .
14.如图,在平面直角坐标系xOy内有一点Q(3,4),那么射线OQ与x轴正半轴的夹角α的余弦值是 .
15.某处欲建一观景平台,如图所示,原设计平台的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°,则调整后楼梯AD的长为 m.(结果保留根号)
(15题图) (16题图) (17题图)
16.如图,一山坡的坡度为i=1:,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了 米.
17.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为 米.(精确到1米,参考数据:≈1.73)
三.解答题(共5小题)
18.如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,BE=1,求cosA的值.
19.如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
20.芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,≈1.732)
21.如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为1:(即AB:BC=1:),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
青岛版九年级数学上册第二单元复习题
参考答案与试题解析
一.选择题(共12小题)
1.B.2.D.3.B.4.D.5.C.6.A.7.D.8.A.9.A.10.B.
11.B.12.C.
二.填空题(共5小题)
13.2 14. 15.6 16. 100 17. 208
三.解答题(共5小题)
18.(1)证明:连接AD、OD
∵AC是直径
∴AD⊥BC
∵AB=AC
∴D是BC的中点
又∵O是AC的中点
∴OD∥AB
∵DE⊥AB
∴OD⊥DE
∴DE是⊙O的切线
(2)解:由(1)知OD∥AE,
∴∠FOD=∠FAE,∠FDO=∠FEA,
∴△FOD∽△FAE,
∴
∴
∴
解得FC=2
∴AF=6
∴Rt△AEF中,cos∠FAE====.
19.解:作BE⊥l于点E,DF⊥l于点F.
根据题意,得BE=24mm,DF=48mm.
在Rt△ABE中,sin ,
∴mm
在Rt△ADF中,cos ,
∴mm.
∴矩形ABCD的周长=2(40+60)=200mm.
20.解:设DH=x米,
∵∠CDH=60°,∠H=90°,
∴CH=DH?sin60°=x,
∴BH=BC+CH=2+x,
∵∠A=30°,
∴AH=BH=2+3x,
∵AH=AD+DH,
∴2+3x=20+x,
解得:x=10﹣,
∴BH=2+(10﹣)=10﹣1≈16.3(米).
答:立柱BH的长约为16.3米.
21.解:∵AF⊥AB,AB⊥BE,DE⊥BE,
∴四边形ABEF为矩形,
∴AF=BE,EF=AB=2
设DE=x,在Rt△CDE中,CE===x,
在Rt△ABC中,
∵=,AB=2,
∴BC=2,
在Rt△AFD中,DF=DE﹣EF=x﹣2,
∴AF===(x﹣2),
∵AF=BE=BC+CE.
∴(x﹣2)=2+x,
解得x=6.
答:树DE的高度为6米.
一.选择题(共12小题)
1.如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于( )
A. B. C. D.
(1题图) (6题图) (7题图) (9题图)
2.在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,下列各式成立的是( )
A.b=a?sinB B.a=b?cosB C.a=b?tanB D.b=a?tanB
3.计算cos30°的值为( )
A. B. C.1 D.3
4.在△ABC中,(2cosA﹣)2+|1﹣tanB|=0,则△ABC一定是( )
A.直角三角形 B.等腰三角形
C.等边三角形 D.等腰直角三角形
5.在Rt△ABC中,∠C=90°,sinA=,AC=6cm,则BC的长度为( )
A.6cm B.7cm C.8cm D.9cm
6.如图,△ABC中,AC=5,cosB=,sinC=,则△ABC的面积为( )
A. B.12 C.14 D.21
7.如图,小颖利用一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是( )
A.4m B.m C.(5+)m D.(+)m
8.一辆汽车沿坡角为α的斜坡前进500米,则它上升的最大高度为( )
A.500sinα B. C.500cosα D.
9.如图,为了测量某建筑物MN的高度,在平地上A处测得建筑物顶端M的仰角为30°,向N点方向前进16m到达B处,在B处测得建筑物顶端M的仰角为45°,则建筑物MN的高度等于( )
A.8()m B.8()m C.16()m D.16()m
10.如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )
A.22.48 B.41.68 C.43.16 D.55.63
(10题图) (11题图) (12题图) (13题图) (14题图)
11.如图,一艘轮船在B处观测灯塔A位于南偏东50°方向上,相距40海里,轮船从B处沿南偏东20°方向匀速航行至C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
A.20海里 B.40海里 C.20海里 D.40海里
12.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A. B.2 C. D.
二.填空题(共5小题)
13.如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD= .
14.如图,在平面直角坐标系xOy内有一点Q(3,4),那么射线OQ与x轴正半轴的夹角α的余弦值是 .
15.某处欲建一观景平台,如图所示,原设计平台的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°,则调整后楼梯AD的长为 m.(结果保留根号)
(15题图) (16题图) (17题图)
16.如图,一山坡的坡度为i=1:,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了 米.
17.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为 米.(精确到1米,参考数据:≈1.73)
三.解答题(共5小题)
18.如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,BE=1,求cosA的值.
19.如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
20.芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,≈1.732)
21.如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为1:(即AB:BC=1:),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
青岛版九年级数学上册第二单元复习题
参考答案与试题解析
一.选择题(共12小题)
1.B.2.D.3.B.4.D.5.C.6.A.7.D.8.A.9.A.10.B.
11.B.12.C.
二.填空题(共5小题)
13.2 14. 15.6 16. 100 17. 208
三.解答题(共5小题)
18.(1)证明:连接AD、OD
∵AC是直径
∴AD⊥BC
∵AB=AC
∴D是BC的中点
又∵O是AC的中点
∴OD∥AB
∵DE⊥AB
∴OD⊥DE
∴DE是⊙O的切线
(2)解:由(1)知OD∥AE,
∴∠FOD=∠FAE,∠FDO=∠FEA,
∴△FOD∽△FAE,
∴
∴
∴
解得FC=2
∴AF=6
∴Rt△AEF中,cos∠FAE====.
19.解:作BE⊥l于点E,DF⊥l于点F.
根据题意,得BE=24mm,DF=48mm.
在Rt△ABE中,sin ,
∴mm
在Rt△ADF中,cos ,
∴mm.
∴矩形ABCD的周长=2(40+60)=200mm.
20.解:设DH=x米,
∵∠CDH=60°,∠H=90°,
∴CH=DH?sin60°=x,
∴BH=BC+CH=2+x,
∵∠A=30°,
∴AH=BH=2+3x,
∵AH=AD+DH,
∴2+3x=20+x,
解得:x=10﹣,
∴BH=2+(10﹣)=10﹣1≈16.3(米).
答:立柱BH的长约为16.3米.
21.解:∵AF⊥AB,AB⊥BE,DE⊥BE,
∴四边形ABEF为矩形,
∴AF=BE,EF=AB=2
设DE=x,在Rt△CDE中,CE===x,
在Rt△ABC中,
∵=,AB=2,
∴BC=2,
在Rt△AFD中,DF=DE﹣EF=x﹣2,
∴AF===(x﹣2),
∵AF=BE=BC+CE.
∴(x﹣2)=2+x,
解得x=6.
答:树DE的高度为6米.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
