数学湘教版必修1： 复合函数单调性

课件24张PPT。复合函数单调性-2复习准备 对于给定区间I上的函数f(x)，若对于I上的任意两个值x1,x2，当x1)f(x2),则称f(x)是I上的增（减）函数，区间I称为f(x)的增（减）区间。1、函数单调性的定义是什么？复习准备1、函数单调性的定义是什么？2、证明函数单调性的步骤是什么？ 证明函数单调性应该按下列步骤进行：
第一步：取值
第二步：作差
第三步：变形
第四步：定号
第五步：判断下结论复习准备1、函数单调性的定义是什么？2、证明函数单调性的步骤是什么？3、现在已经学过的判断函数单调性有些什么方法？图象法.定义法; 正比例函数：y=kx　 (k≠0)
反比例函数：y=k/x　 (k≠0)
一次函数ｙ＝kx＋b (k≠0) 　
二次函数y=ax2+bx+c (a≠0)
另:结论1：y＝f(x)(f(x) 恒不为0），与 的单调性相反。例1：判断函数在(1,+∞)上的单调性。复合函数单调性:1.利用已知函数单调性进行判断例2：设f(x)在定义域A上是减函数，试判断y＝3－2f(x)在A上的单调性，并说明理由。解：y=3－2f(x)在A上是增函数，因为：
任取x1，x2∈A，且x1由f(x)在A上为减函数，所以
f(x1)>f(x2),故－2 f(x1)<－2f(x2) 所以3－2 f(x1)<3－2f(x2)即有
y1 y＝f(x)与y＝kf(x)
当k>0时，单调性相同；
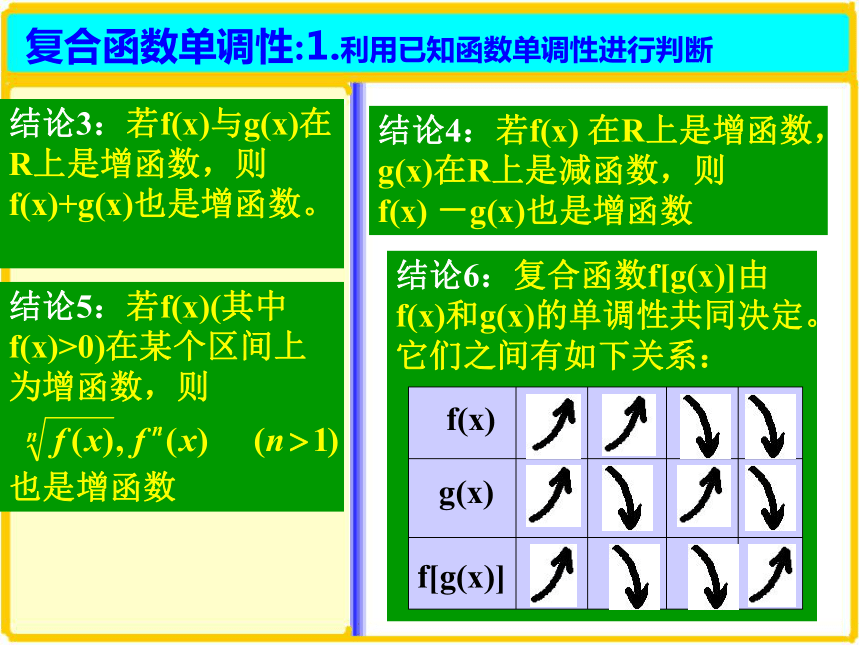
当k<0时，单调性相反。复合函数单调性:1.利用已知函数单调性进行判断结论3：若f(x)与g(x)在R上是增函数，则f(x)+g(x)也是增函数。结论4：若f(x) 在R上是增函数， g(x)在R上是减函数，则
f(x) －g(x)也是增函数结论5：若f(x)(其中f(x)>0)在某个区间上为增函数，则
也是增函数结论6：复合函数f[g(x)]由f(x)和g(x)的单调性共同决定。它们之间有如下关系：
复合函数单调性:1.利用已知函数单调性进行判断复合函数单调性:2.单调区间的求法例3：设y=f(x)的单增区间是(2,6)，求函数y=f(2－x)的单调区间。练习2：求函数的单调区间。答案：
[2, 5]单减区间
[-1,2]单增区间注意：求单调区间时，一定要先看定义域。复合函数单调性:2.单调区间的求法3.函数单调性解题应用例4：已知函数
y=x2－2ax＋a2－1在(－∞,1)上是减函数，求a的取值范围。解此类由二次函数单调性求参数范围的题，最好将二次函数的图象画出来，通过图象进行分析，可以将抽象的问题形象化。练习：如果
f(x)=x2－(a－1)x+5在区间（0.5，1）上是增函数，那么
f(2)的取值范围是什么？答案：[7,＋∞）例5：已知x∈[0,1],则函数
的最大值为_______
最小值为_________ 利用函数的单调性求函数的值域，这是求函数值域和最值的又一种方法。3.函数单调性解题应用例6：已知：f(x)是定义在[－1,1]上的增函数，且f(x－1)求x的取值范围。注： 在利用函数的单调性解不等式的时候，一定要注意定义域的限制。
保证实施的是等价转化3.函数单调性解题应用例7：已知f(x)在其定义域R＋上为增函数，
f(2)=1,f(xy)=f(x)+f(y).解不等式
f(x)+f(x－2) ≤3 解此类题型关键在于充分利用题目所给的条件，本题就抓住这点想办法构造出f(8)=3,这样就能用单调性解不等式了。4.函数单调性解题应用已知函数f(x)定义在(0, +∞)上是单调递增,满足(1)f(xy) = f(x) + f(y); (2)f(2) = 1; (3)f(x) + f(x +３)≤2,则x∈________.解：∵f(xy) = f(x) + f(y) f(2) = 1又∵f(x)在(0, + ∞)上递增.∴f(x) + f(x + 3)≤2 即是f[x(x +３)] ≤f(2) + f(2) = f(4)小结1、怎样用定义证明函数的单调性？2、判断函数的单调性有哪些方法？3、与单调性有关的题型大致有哪些？取值作差变形定号下结论小结1、怎样用定义证明函数的单调性？2、判断函数的单调性有哪些方法？3、与单调性有关的题型大致有哪些？小结1、怎样用定义证明函数的单调性？2、判断函数的单调性有哪些方法？3、与单调性有关的题型大致有哪些？证明: ∵函数f (x)的定义域为R.解法一：∴设x1,x2∈R且x1< x2则