3.3 一元一次方程的解法 课件

课件37张PPT。3.3 一元一次方程的解法合并同类项与移项：
1.怎样合并同类项？(ax=b的形式)
2.什么叫做移项，需要注意
什么？
3.掌握解方程的一般步骤
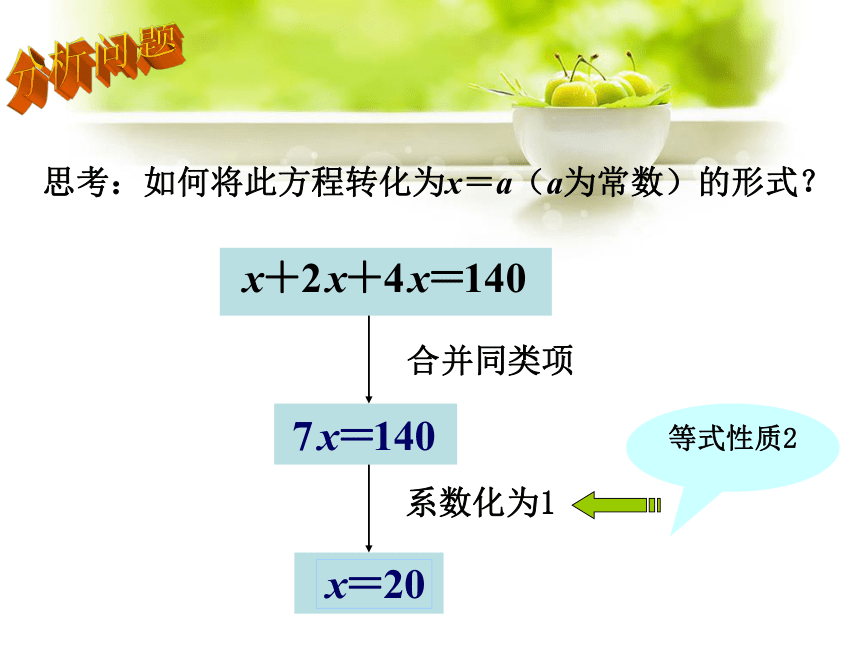
4.用方程解决实际问题思路是什么？问题1：某校三年共购买计算机140台，去年购买数量是前年的2倍，今年购买数量又是去年的2倍．前年这个学校购买了多少台计算机？设去年购买计算机x台.设今年购买计算机x台.方法1：方法2：提出问题思考：如何将此方程转化为x＝a（a为常数）的形式？合并同类项系数化为1等式性质2分析问题合并同类项，得系数化为1，得解：例把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺25本.这个班有多少学生？提出问题1、设未知数：设这个班有x名学生.2、找相等关系
这批书的总数是一个定值，表示它的两个等式相等3、列方程
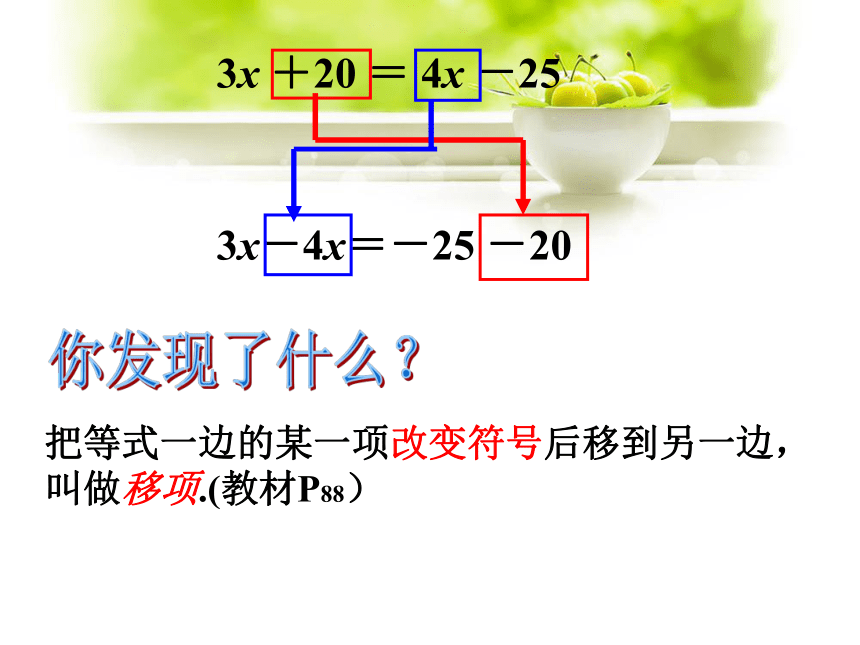
3x＋20 = 4x－25分析问题把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺25本.这个班有多少学生？每人分3本，共分出3x本，加上剩余的20本，这批书共 本.每人分4本，需要____ 本，减去缺的25本，
这批书共 本. 3x＋204x4x－25提问：怎样解这个方程？它与上节课遇到的方程有何不同？3x＋20 = 4x－25方程的两边都有含x的项（3x与4x）和不含字母的常数项（20与－25）.3x+20=4x-253x+20-4x=4x-25－4x3x+20-4x= -253x+20-4x－20=-25－203x-4x=-25－20（合并同类项）（利用等式性质1） （利用等式性质1） （合并同类项）提问：如何才能使这个方程向x=a的形式转化？你发现了什么？3x ＋20 ＝ 4x －253x－4x＝－25 －20把等式一边的某一项改变符号后移到另一边，叫做移项.(教材P88）3x+20=4x-253x-4x=-25-20-x=-45x =45移项合并同类项系数化为1下面的框图表示了解这个方程的具体过程：通过移项，使等号左边仅含未知数的项，等号右边仅含常数的项，使方程更接近x=a的形式. 提问： “移项”起了什么作用？提问：以上解方程“移项”的依据是什么？移项的依据是等式的性质1例某制药厂制造一批药品，如用旧工艺，则废水排量要比环保限制的最大量还多200t；如用新工艺，则废水排量要比环保限制的最大量少100t.新、旧工艺的废水排量之比为2:5，两种工艺的废水排量各是多少？
解：设新、旧工艺的废水排量分别为2xt和5xt.
根据废水排量与环保限制最大量之间的关系，得
5x-200=2x+100.
移项，得5x-2x=100+200.
合并同类项，得3x=300.
系数化为1，得x=100.
所以2x=200，5x=500.
等号两边代表哪些数量？例：解下列方程 解：移项，得
即
系数化为1，得 x = - 2
（2）解：移项，得
合并同类项，得

系数化为1，得
（1） 移项时应注意改变项的符号运用新知“移项”应注意什么？巩固练习解下列方程：（1）10x－3＝9（2）6x－7＝4x － 5有一个班的同学去划船，他们算了一下，如果增加一条船，正好每条船坐6人，如果减少一条船 ，正好每条船坐9人，问：这个班共多少同学？ 综合应用解法一：设船有x条.则
6(x+1)=9(x-1)
得出 x=5
6× (5+1)=36（人）
答：这个班共有36人.有一个班的同学去划船，他们算了一下，如果增加一条船，正好每条船坐6人，如果减少一条船 ，正每条船坐9人，问：这个班共多少同学？ 解法二：设这个班共有同学x人.则
得出 x=36
答：这个班共有36人.1、已知2x＋１与－12x＋5的值是相反数，求ｘ的值.拓展思维2、已知：y1 = 2x+1， y2 = 3 －x.当x取何值时， y1 = y2 ？ 阿尔-花拉子米（约780——约850）中世纪阿拉伯数学家.出生波斯北部城市花拉子模（现属俄罗斯），曾长期生活于巴格达，对天文、地理、历法等方面均有所贡献.它的著作通过后来的拉丁文译本，对欧洲近代科学的诞生产生过积极影响. 《对消与还原》 现在你能回答前面提到的古老的代数书中的“对消”与“还原”是什么意思吗？“对消”与“还原”就是“合并”与“移项”去括号与去分母1、掌握用分配律、去括号法则解含括号的一元一次方程的方法.
2、会抓住实际问题中的等量关系列一元一次方程解决实际问题.学习目标回顾：你还记得分配律吗？用字母怎样表示？一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加．a(b+c)=ab+ac小练习：
１、2（x+8）
2、-3（3x+4）
3、-（7y-5)
2x+16-9x-12-7y+5注意符号注意符号 某工厂加强节能措施，去年下半年与上半年相比，月平均用电量减少2000度，全年用电15万度，这个工厂去年上半年每月平均用电多少度？分析：若设上半年每月平均用电x度，
则下半年每月平均用电 度
上半年共用电 度，
下半年共用电 度因为全年共用了15万度电，
所以，可列方程 . （x-2000）6（x-2000）6x6x+ 6（x-2000）=150000问题： 解：设上半年每月平均用电x度，则下半年每月平均用电（x-2000）度，上半年共用电6x度，下半年共用电6（x-2000）度.
根据题意列方程得：6x+ 6（x-2000）=150000去括号得：6x+6x-12000=150000移项得：6x+6x=150000+12000合并同类项得：12x=162000系数化为1得：x=13500答:这个工厂去年上半年每月平均用电13500度.去括号法则：
⑴括号前是“+”号，把括号和它前面的“+”号去掉，括号里各项都不变符号.
⑵括号前是“－”号，把括号和它前面的“－”号去掉，括号里各项都改变符号探究：如果设去年下半年平均每月用电y度，那么上半年平均每月用电 度.根据等量关系： ，可列方程：(y+2000)上半年用电量+下半年用电量=1500006（y+2000）+6y=150000那么上半年平均每月用电量为：11500+2000=13500（度）答：去年上半年平均每月用电13500度. ▲用一元一次方程解决实际问题的一般步骤：⑴ 读题、审题后，找出实际问题中的等量关系.⑵ 根据找出的等量关系，设未知数，列方程，把实际为题转化成数学问题.⑶ 解方程后，验证解的合理性，再作答.解方程:3x-7(x-1)=3-2(x+3)解：去括号，得3x-7x+7=3-2x-6移项，得3x-7x+2x=3-6-7合并同类项，得-2x=-10系数化成１，得x=5例： 1、解方程: 3-（4x-3）＝7
解：去括号，得移项，得 合并同类项，得 系数化成１，得及时练习12、下列变形对吗？若不对，请说明理由，并改正：
解方程
去括号，得
移项，得
合并同类项，得
两边同除以-0.2得
去括号变形错，有一项
没变号，改正如下：挑战自我英国伦敦博物馆保存着一部极其珍贵的文物
纸莎草文书.这是古代埃及人用象形文字写在一种
特殊的草上的著作，至今已有三千七百多年.书中记
载了许多与方程有关的数学问题.其中有如下一道
著名的求未知数的问题:问题一个数，它的三分之二，它的一半，它的七分
之一，它的全部，加起来总共是33.试问这个
数是多少？你能解决这个问题吗？你知道吗？丢番图的墓志铭: “坟中安葬着丢番图，多么令人惊讶，它忠实地记录
了所经历的道路.上帝给予的童年占六分之一.又
过十二分之一，两颊长胡.再过七分之一，点燃结婚
的蜡烛.五年之后天赐贵子，可怜迟到的宁馨儿，享
年仅及其父之半，便进入冰冷的墓.悲伤只有用数论
的研究去弥补，又过四年，他也走完了人生的旅途.”你知道丢番图去世时的年龄吗？请你列出方程
来算一算.试一试思考去分母去分母，得14x+7x+12x+420+42x+336 = 84x移项，得14x+7x+12x+42x - 84x = - 420 - 336合并，得 - 9x = - 756系数化为1，得 x = 84答：丢番图去世是的年龄是84岁.去分母的关键是在于：方程的两边同时乘以各分母的最小公倍数，化为整系数方程.解：设丢番图去世的年龄为x岁，由题意，得解方程:去分母时要 注意什么问题？(1)方程两边每一项都要乘以各分母的最小
公倍数(2)去分母后如分子中含有两项，应将该分子
添上括号典型例析想一想去分母（方程两边同乘以各分母的最小公倍数）去括号移项合并系数化为1解：去分母，得
18x+3(x-1) =18－2 (2x -1)
去括号 18x ＋3x－3= 18－4x +2
移项 18x +3x ＋ 4x = 18 +2＋3
合并同类项 25x = 23
系数化为1 x=例：★去括号、移项、合并同类项、系数为化1，要注意的几个问题：③ 合并同类项时，只是把同类项的系数相加作为所得项的系数，字母部分不变.
④系数化为1，要方程两边同时除以未知数前面的系数.②移项要变号.
①去括号要注意括号外的正、负符号.再见！