复数的加减法及几何意义
图片预览





文档简介
课件18张PPT。3.2 复数代数形式的四则运算3.2.1
复数代数形式的加减运算及其几何意义 我们引入这样一个数i ,把i 叫做虚数单位,并且规定: i2??1; 形如a+bi(a,b∈R)的数叫做复数. 全体复数所形成的集合叫做复数集,一般用字母C表示 .知识回顾对虚数单位i 的规定 练习. 根据对虚数单位 i 的规定把下列运算的结果都化
为 a+bi(a、b?R)的形式.
3(2+i)= ; (3-i)i= ;i = ;
-5= ;0= ;2-i= .6+3i1+3i0+i-5+0i0+0i2+(-1)i (1)i2??1;
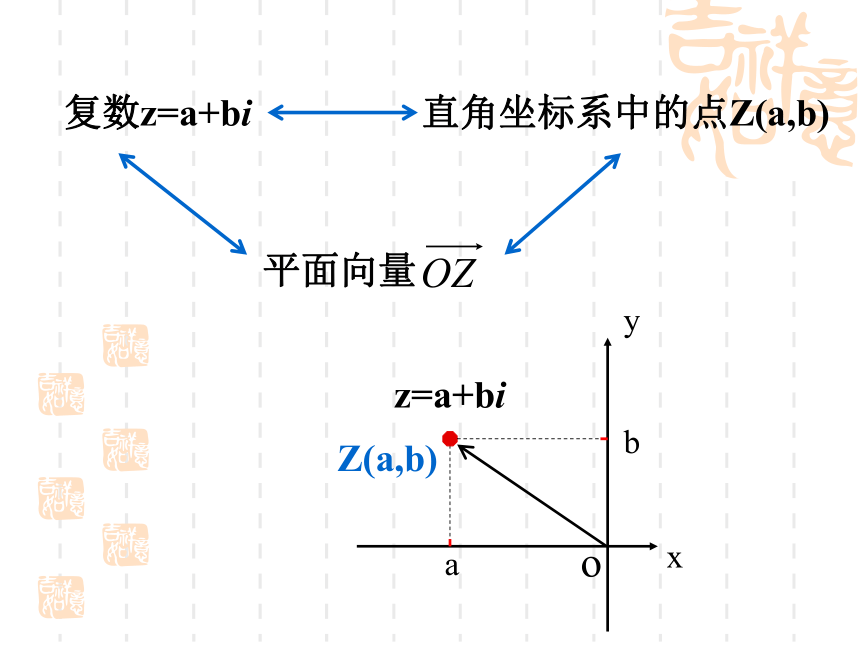
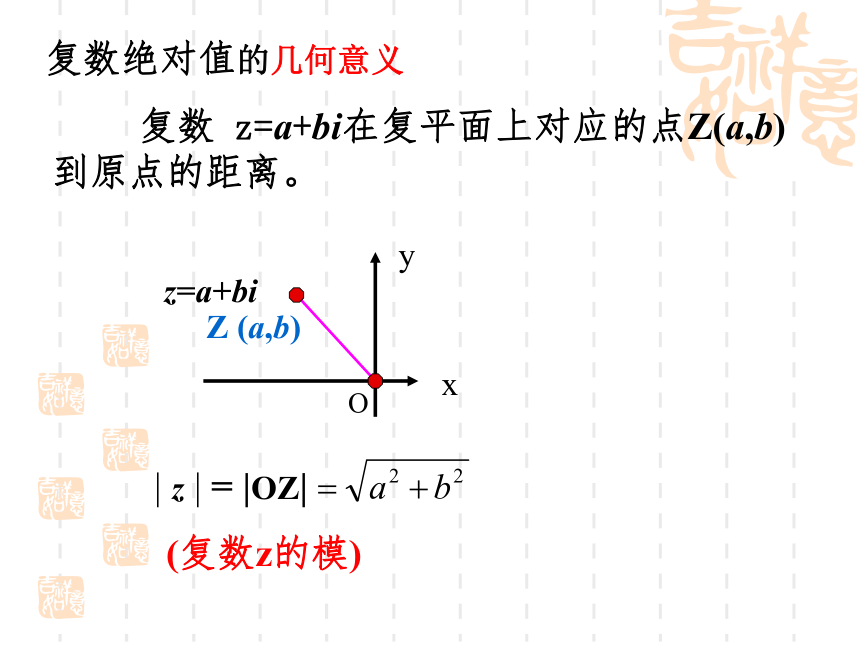
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立。1.复数的代数形式:通常用字母 z 表示,即其中 称为虚数单位。2.复数的分类:非纯虚数纯虚数虚数实数 3.规定:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.注:2) 一般来说,两个复数只能说相等或不相等,而不能比较大小了.复数z=a+bi直角坐标系中的点Z(a,b)平面向量 复数绝对值的几何意义 复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。1.复数加、减法的运算法则:已知两复数z1=a+bi, z2=c+di(a,b,c,d是实数) 即:两个复数相加(减)就是
实部与实部,虚部与虚部分别相加(减).(1)加法法则:z1+z2=(a+c)+(b+d)i; (2)减法法则:z1-z2=(a-c)+(b-d)i. (a+bi )±(c+di) = (a±c) + (b±d)i例1.计算 解:练习、计算(1) (1+3i)+(-4+2i)
(2) (1-3i )+(2+5i) +(-4+9i)
(3) 已知(3-ai)-(b+4i)=2a-bi,
求实数a、b的值。 我们知道,两个向量的和满足平行四边形法则, 复数可以表示平面上的向量,那么复数的加法与向量的加法是否具有一致性呢?xoyZ1(a,b)Z2(c,d)Z(a+c,b+d)符合向量加法的平行四边形法则.1.复数加法运算的几何意义?xoyZ1(a,b)Z2(c,d)符合向量减法的三角形法则.2.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1 ,Z2的距离(1)|z-(1+2i)|(2)|z+(1+2i)| 已知复数z对应点A,说明下列各式所表示的几何意义.点A到点(1,2)的距离点A到点(-1, -2)的距离(3)|z-1|(4)|z+2i|点A到点(1,0)的距离点A到点(0, -2)的距离练习:已知复数m=2-3i,若复数z满足不等式|z-m|=1,则z所对应的点的集合是什么图形?以点(2, -3)为圆心,
1为半径的圆上1、|z1|= |z2|
平行四边形OABC是2、| z1+ z2|= | z1- z2|
平行四边形OABC是3、 |z1|= |z2|,| z1+ z2|= | z1- z2|
平行四边形OABC是oz2-z1ABC菱形矩形正方形3、复数加减法的几何意义练习:设z1,z2∈C, |z1|= |z2|=1
|z2+z1|= 求|z2-z1|
复数代数形式的加减运算及其几何意义 我们引入这样一个数i ,把i 叫做虚数单位,并且规定: i2??1; 形如a+bi(a,b∈R)的数叫做复数. 全体复数所形成的集合叫做复数集,一般用字母C表示 .知识回顾对虚数单位i 的规定 练习. 根据对虚数单位 i 的规定把下列运算的结果都化
为 a+bi(a、b?R)的形式.
3(2+i)= ; (3-i)i= ;i = ;
-5= ;0= ;2-i= .6+3i1+3i0+i-5+0i0+0i2+(-1)i (1)i2??1;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立。1.复数的代数形式:通常用字母 z 表示,即其中 称为虚数单位。2.复数的分类:非纯虚数纯虚数虚数实数 3.规定:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.注:2) 一般来说,两个复数只能说相等或不相等,而不能比较大小了.复数z=a+bi直角坐标系中的点Z(a,b)平面向量 复数绝对值的几何意义 复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。1.复数加、减法的运算法则:已知两复数z1=a+bi, z2=c+di(a,b,c,d是实数) 即:两个复数相加(减)就是
实部与实部,虚部与虚部分别相加(减).(1)加法法则:z1+z2=(a+c)+(b+d)i; (2)减法法则:z1-z2=(a-c)+(b-d)i. (a+bi )±(c+di) = (a±c) + (b±d)i例1.计算 解:练习、计算(1) (1+3i)+(-4+2i)
(2) (1-3i )+(2+5i) +(-4+9i)
(3) 已知(3-ai)-(b+4i)=2a-bi,
求实数a、b的值。 我们知道,两个向量的和满足平行四边形法则, 复数可以表示平面上的向量,那么复数的加法与向量的加法是否具有一致性呢?xoyZ1(a,b)Z2(c,d)Z(a+c,b+d)符合向量加法的平行四边形法则.1.复数加法运算的几何意义?xoyZ1(a,b)Z2(c,d)符合向量减法的三角形法则.2.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1 ,Z2的距离(1)|z-(1+2i)|(2)|z+(1+2i)| 已知复数z对应点A,说明下列各式所表示的几何意义.点A到点(1,2)的距离点A到点(-1, -2)的距离(3)|z-1|(4)|z+2i|点A到点(1,0)的距离点A到点(0, -2)的距离练习:已知复数m=2-3i,若复数z满足不等式|z-m|=1,则z所对应的点的集合是什么图形?以点(2, -3)为圆心,
1为半径的圆上1、|z1|= |z2|
平行四边形OABC是2、| z1+ z2|= | z1- z2|
平行四边形OABC是3、 |z1|= |z2|,| z1+ z2|= | z1- z2|
平行四边形OABC是oz2-z1ABC菱形矩形正方形3、复数加减法的几何意义练习:设z1,z2∈C, |z1|= |z2|=1
|z2+z1|= 求|z2-z1|
