21.3二次函数与一元二次方程课件(共18张PPT)
文档属性
| 名称 | 21.3二次函数与一元二次方程课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-29 00:00:00 | ||
图片预览





文档简介
课件18张PPT。21.3二次函数与一元二次方程沪科版九年级数学上册 一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=______。
一元二次方程根的情况是:
当△﹥0 时,方程 ;
当△=0时,方程 ;
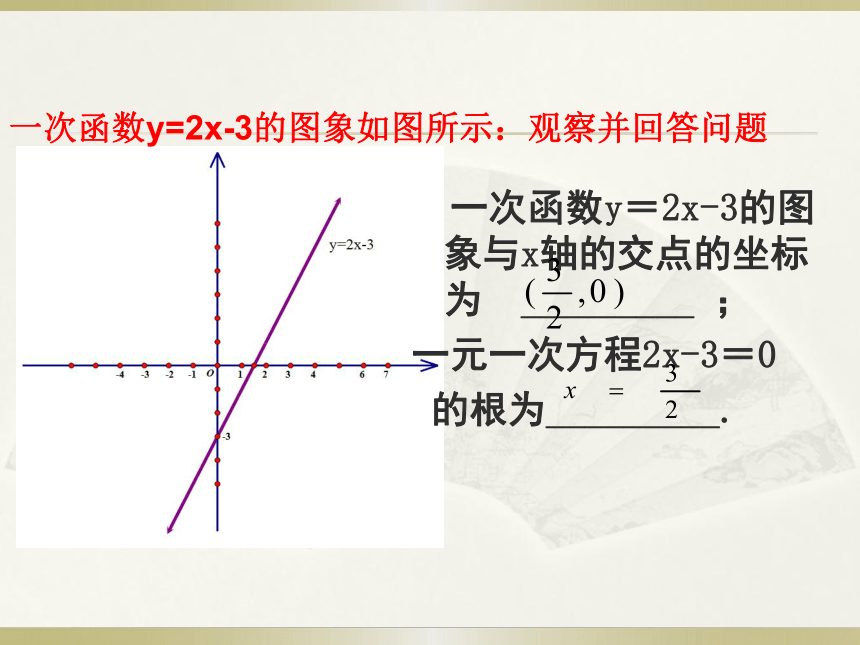
当△﹤0时,方程 。b2-4ac有两个不等实数根有两个相等实数根没有实数根 一次函数y=2x-3的图象与x轴的交点的坐标为 _________ ;
一元一次方程2x-3=0
的根为_________.
一次函数y=2x-3的图象如图所示:观察并回答问题
结论:一次函数y=kx+b(k≠0)的图象与x轴的交点的横坐标就是一元一次方程kx+b=0(k≠o)的根.
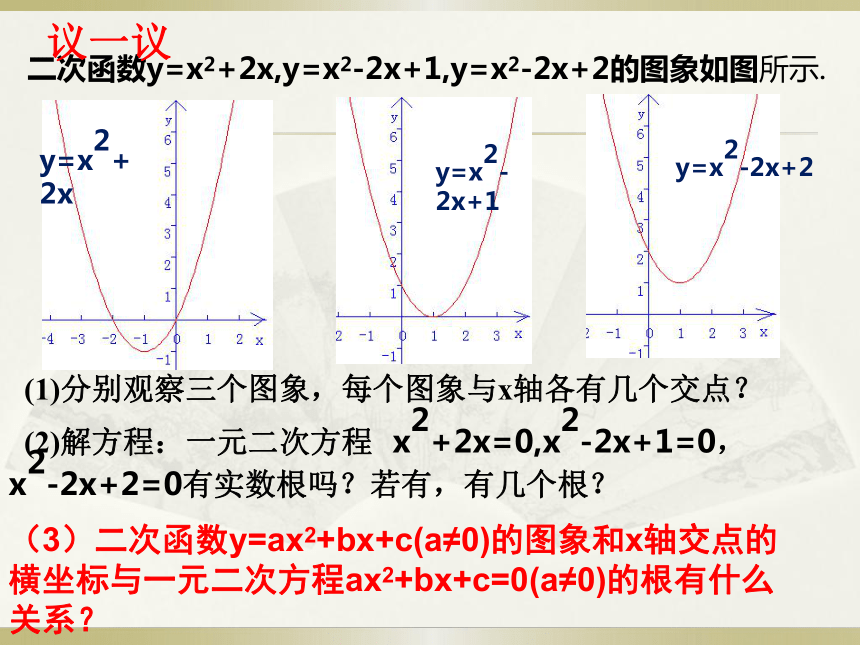
通过观察对比,一次函数y=kx+b (k≠0)的图象与x轴的交点的坐标与一元一次方程kx+b=0的根有什么关系?探究新知 问题:一元二次方程ax2+bx+c=0(a≠0)和二次函数y=ax2+bx+c(a≠0)之间是否也存在一定的关系呢? (1)分别观察三个图象,每个图象与x轴各有几个交点?
(2)解方程:一元二次方程 x2+2x=0,x2-2x+1=0,
x2-2x+2=0有实数根吗?若有,有几个根?
二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示.y=x2+2xy=x2-2x+1y=x2-2x+2议一议(3)二次函数y=ax2+bx+c(a≠0)的图象和x轴交点的横坐标与一元二次方程ax2+bx+c=0(a≠0)的根有什么关系? 二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0根的关系?有两个不相等的实数根b2-4ac > 0有两个相等的实数根b2-4ac = 0没有实数根b2-4ac < 0有两个交点有一个交点没有交点结论:二次函数y=ax2+bx+c(a ≠ 0)与x轴交点的横坐标即为二次方程ax2+bx+c=0 (a ≠ 0)的根。探究二:二次函数y=ax2+bx+c与x轴的交点个数与一元二次方程ax2+bx+c=0的解有关系吗?结论:
函数与x轴有两个交点 方程有两不相等根
函数与x轴有一个交点 方程有两相等根
函数与x轴没有交点 方程没有根
方程的根的情况是由什么决定的?
判别式b2-4ac的符号
结论:
对于二次函数y=ax2+bx+c,判别式又能给我们什么样的结论?
(1)b2-4ac>0 函数图像与x轴有两个交点
(2)b2-4ac=0 函数图像与x轴有一个交点
(3)b2-4ac<0 函数图像与x轴没有交点
例 1、不画图象,判断下列函数的图象与x轴是否有公共点,并说明理由. ∴此方程有两个不相等的实数根.
∴该抛物线与x轴有两个交点. ∴此方程没有实数根.
∴该抛物线与x轴没有公共点.
例2、求二次函数图象与X轴交点的坐标: 1、方程 的根是____________
则函数 的图象与x轴的交点有 个,其坐
标是 . 2(2,0)、(4,0)大显身手
2、方程 的根是 ;则函数
的 图象与x轴的交点有 个,其坐标是 . 3、下列函数的图象中,与x轴没有公共点的是( )1(6,0)Dx1=2,X2=44、抛物线y=x2+7x+6与y轴的交点坐标是 , 与x轴的交点坐标是 . (-1,0),(-6,0)(0,6)5、已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的解是 .5x1=0,X2=5课堂练习交流总结同学们:
通过这节课的学习,你收获了什么?1、二次函数与一元二次方程的关系
一般地,关于x的一元二次方ax2+bx+c=0(a≠0)的根,就是二次函数y=ax2+bx+c(a≠0)的值为0时自变量x的值,也就是函数y=ax2+bx+c的图象与x轴交点的横坐标。
2、二次函数y=ax2+bx+c与X轴交点个数的确定
可由一元二次方程的根的判别式来判定二次函数图象与x轴的交点的情况,由根与系数的关系来解决相关问题。
在函数问题中,往往需要解方程:反过来也可以利用函数图象解方程。两种思想:函数与方程互相转化的思想;数形结合思想.
作业习题21.3 第1、2、3题祝同学们学心进步! 已知二次函数y=kx2-7x-7的图象与x轴有交点,求k的取值范围. 点拨:①因为是二次函数,因而k≠0;
②有交点,所以应为△≥0.错解:由△=(-7)2-4×k×(-7)=49+28k>0,
得k>- .正确解法:此函数为二次函数,∴k≠0,
又与x轴有交点,∴△=(-7)2-4×k×(-7)= 49+28k≥0, 得k≥- ,即k≥ - 且k≠0 拓展练习
一元二次方程根的情况是:
当△﹥0 时,方程 ;
当△=0时,方程 ;
当△﹤0时,方程 。b2-4ac有两个不等实数根有两个相等实数根没有实数根 一次函数y=2x-3的图象与x轴的交点的坐标为 _________ ;
一元一次方程2x-3=0
的根为_________.
一次函数y=2x-3的图象如图所示:观察并回答问题
结论:一次函数y=kx+b(k≠0)的图象与x轴的交点的横坐标就是一元一次方程kx+b=0(k≠o)的根.
通过观察对比,一次函数y=kx+b (k≠0)的图象与x轴的交点的坐标与一元一次方程kx+b=0的根有什么关系?探究新知 问题:一元二次方程ax2+bx+c=0(a≠0)和二次函数y=ax2+bx+c(a≠0)之间是否也存在一定的关系呢? (1)分别观察三个图象,每个图象与x轴各有几个交点?
(2)解方程:一元二次方程 x2+2x=0,x2-2x+1=0,
x2-2x+2=0有实数根吗?若有,有几个根?
二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示.y=x2+2xy=x2-2x+1y=x2-2x+2议一议(3)二次函数y=ax2+bx+c(a≠0)的图象和x轴交点的横坐标与一元二次方程ax2+bx+c=0(a≠0)的根有什么关系? 二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0根的关系?有两个不相等的实数根b2-4ac > 0有两个相等的实数根b2-4ac = 0没有实数根b2-4ac < 0有两个交点有一个交点没有交点结论:二次函数y=ax2+bx+c(a ≠ 0)与x轴交点的横坐标即为二次方程ax2+bx+c=0 (a ≠ 0)的根。探究二:二次函数y=ax2+bx+c与x轴的交点个数与一元二次方程ax2+bx+c=0的解有关系吗?结论:
函数与x轴有两个交点 方程有两不相等根
函数与x轴有一个交点 方程有两相等根
函数与x轴没有交点 方程没有根
方程的根的情况是由什么决定的?
判别式b2-4ac的符号
结论:
对于二次函数y=ax2+bx+c,判别式又能给我们什么样的结论?
(1)b2-4ac>0 函数图像与x轴有两个交点
(2)b2-4ac=0 函数图像与x轴有一个交点
(3)b2-4ac<0 函数图像与x轴没有交点
例 1、不画图象,判断下列函数的图象与x轴是否有公共点,并说明理由. ∴此方程有两个不相等的实数根.
∴该抛物线与x轴有两个交点. ∴此方程没有实数根.
∴该抛物线与x轴没有公共点.
例2、求二次函数图象与X轴交点的坐标: 1、方程 的根是____________
则函数 的图象与x轴的交点有 个,其坐
标是 . 2(2,0)、(4,0)大显身手
2、方程 的根是 ;则函数
的 图象与x轴的交点有 个,其坐标是 . 3、下列函数的图象中,与x轴没有公共点的是( )1(6,0)Dx1=2,X2=44、抛物线y=x2+7x+6与y轴的交点坐标是 , 与x轴的交点坐标是 . (-1,0),(-6,0)(0,6)5、已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的解是 .5x1=0,X2=5课堂练习交流总结同学们:
通过这节课的学习,你收获了什么?1、二次函数与一元二次方程的关系
一般地,关于x的一元二次方ax2+bx+c=0(a≠0)的根,就是二次函数y=ax2+bx+c(a≠0)的值为0时自变量x的值,也就是函数y=ax2+bx+c的图象与x轴交点的横坐标。
2、二次函数y=ax2+bx+c与X轴交点个数的确定
可由一元二次方程的根的判别式来判定二次函数图象与x轴的交点的情况,由根与系数的关系来解决相关问题。
在函数问题中,往往需要解方程:反过来也可以利用函数图象解方程。两种思想:函数与方程互相转化的思想;数形结合思想.
作业习题21.3 第1、2、3题祝同学们学心进步! 已知二次函数y=kx2-7x-7的图象与x轴有交点,求k的取值范围. 点拨:①因为是二次函数,因而k≠0;
②有交点,所以应为△≥0.错解:由△=(-7)2-4×k×(-7)=49+28k>0,
得k>- .正确解法:此函数为二次函数,∴k≠0,
又与x轴有交点,∴△=(-7)2-4×k×(-7)= 49+28k≥0, 得k≥- ,即k≥ - 且k≠0 拓展练习
