23.1锐角的三角函数课件
图片预览





文档简介
课件19张PPT。23.1锐角的三角函数 教学目标:
1、了解正切的概念,并能进行相关的计算。
2、理解坡度、坡比、坡角的定义。
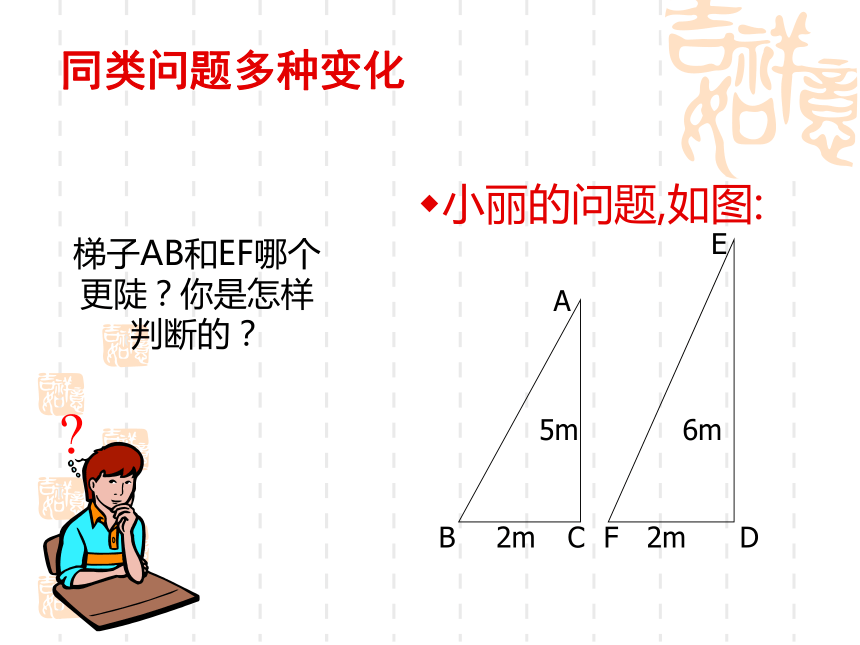
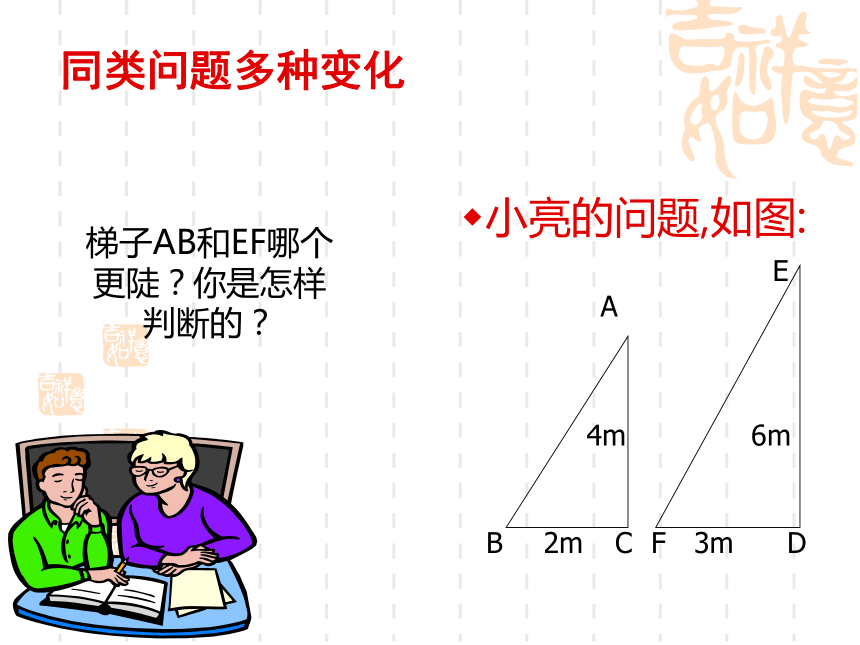
3、知道当锐角固定时,角的对边与邻边的比值总是一个固定值。源于生活的数学从梯子的倾斜程度谈起梯子是我们日常生活中常见的物体你能比较两个梯子哪个更陡吗?你有哪些办法?从生活实践开始小丽的问题,如图:梯子AB和EF哪个更陡?你是怎样判断的?同类问题多种变化同类问题多种变化小明的问题,如图:梯子AB和EF哪个更陡?你是怎样判断的?小颖的问题,如图:?梯子AB和EF哪个更陡?你是怎样判断的?同类问题多种变化小亮的问题,如图:梯子AB和EF哪个更陡?你是怎样判断的?同类问题多种变化小明和小亮这样想,如图:如图,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子AB1的倾斜程度;驶向胜利的彼岸而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子AB1的倾斜程度.你同意小亮的看法吗?同类问题多种变化用心想一想直角三角形的边与角的关系(1).Rt△AB1C1和Rt△AB2C2有什么关系? 如果改变B2在梯子上的位置(如B3C3 )呢?由此你得出什么结论?用心想一想结论:仍能得到
当直角三角形中的锐角确定之后,它的对边与邻边之比也随之确定。知识升华 在Rt△ABC中,如果锐角A确定,那么锐角A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA,即正切的定义坡比(坡面的坡度):坡面的铅直高度h和水平长度l的比
记作i=h:l
坡面与水平面的夹角叫坡角(或称倾斜角)记作a
tanα=i=h:l
总结:坡度越大,坡角α越大
坡面就越陡
lha例题欣赏例1 下图表示两个自动扶梯,哪一个自动 扶梯比较陡?解:甲梯中,乙梯中,∵tanα>tanβ,∴甲梯更陡. 例2.正切在日常生活中的应用很广泛,例如建筑、工程技术等. 正切经常用来描述山坡的坡度、堤坝的坡度.如图,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度 (即tanα)就是:例题欣赏1、 如图,在△ACB中,∠C = 90°,AC = 6,,求BC、AB的长。大胆尝试 练一练大胆尝试 练一练2.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗? 小结与拓展这节课,你学会了什么?正切的定义: 在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
坡面的坡度(坡比)及坡角小结与拓展1.tanA是在直角三角形中定义的,∠A是一个锐
角(注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯
省去“∠”号(注意tanA不表示tan乘以A).
3.tanA是一个比值(直角边之比,注意比的顺序,
且tanA﹥0,无单位).
4.tanA的大小只与∠A的大小有关,而与直角三角
形的边长无关.
5.角相等,则正切值相等;两锐角的正切值相等,
则这两个锐角相等.正切定义中应注意的问题课堂作业
1:书本练习1、2、3题
2:复习本节内容,完成同步练习
3:预习正弦、余弦
1、了解正切的概念,并能进行相关的计算。
2、理解坡度、坡比、坡角的定义。
3、知道当锐角固定时,角的对边与邻边的比值总是一个固定值。源于生活的数学从梯子的倾斜程度谈起梯子是我们日常生活中常见的物体你能比较两个梯子哪个更陡吗?你有哪些办法?从生活实践开始小丽的问题,如图:梯子AB和EF哪个更陡?你是怎样判断的?同类问题多种变化同类问题多种变化小明的问题,如图:梯子AB和EF哪个更陡?你是怎样判断的?小颖的问题,如图:?梯子AB和EF哪个更陡?你是怎样判断的?同类问题多种变化小亮的问题,如图:梯子AB和EF哪个更陡?你是怎样判断的?同类问题多种变化小明和小亮这样想,如图:如图,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子AB1的倾斜程度;驶向胜利的彼岸而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子AB1的倾斜程度.你同意小亮的看法吗?同类问题多种变化用心想一想直角三角形的边与角的关系(1).Rt△AB1C1和Rt△AB2C2有什么关系? 如果改变B2在梯子上的位置(如B3C3 )呢?由此你得出什么结论?用心想一想结论:仍能得到
当直角三角形中的锐角确定之后,它的对边与邻边之比也随之确定。知识升华 在Rt△ABC中,如果锐角A确定,那么锐角A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA,即正切的定义坡比(坡面的坡度):坡面的铅直高度h和水平长度l的比
记作i=h:l
坡面与水平面的夹角叫坡角(或称倾斜角)记作a
tanα=i=h:l
总结:坡度越大,坡角α越大
坡面就越陡
lha例题欣赏例1 下图表示两个自动扶梯,哪一个自动 扶梯比较陡?解:甲梯中,乙梯中,∵tanα>tanβ,∴甲梯更陡. 例2.正切在日常生活中的应用很广泛,例如建筑、工程技术等. 正切经常用来描述山坡的坡度、堤坝的坡度.如图,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度 (即tanα)就是:例题欣赏1、 如图,在△ACB中,∠C = 90°,AC = 6,,求BC、AB的长。大胆尝试 练一练大胆尝试 练一练2.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗? 小结与拓展这节课,你学会了什么?正切的定义: 在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
坡面的坡度(坡比)及坡角小结与拓展1.tanA是在直角三角形中定义的,∠A是一个锐
角(注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯
省去“∠”号(注意tanA不表示tan乘以A).
3.tanA是一个比值(直角边之比,注意比的顺序,
且tanA﹥0,无单位).
4.tanA的大小只与∠A的大小有关,而与直角三角
形的边长无关.
5.角相等,则正切值相等;两锐角的正切值相等,
则这两个锐角相等.正切定义中应注意的问题课堂作业
1:书本练习1、2、3题
2:复习本节内容,完成同步练习
3:预习正弦、余弦
