31.3 用频率估计概率(第1课时)课件
文档属性
| 名称 | 31.3 用频率估计概率(第1课时)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 277.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-29 00:00:00 | ||
图片预览




文档简介
课件10张PPT。九年级数学·下 新课标[冀教]第三十一章 随机事件的概率31.3 用频率估计概率(第1课时)学 习 新 知欣赏著名球星詹姆斯图片,你知道詹姆斯罚球命中率是多少吗?当试验的所有结果不是有限个,或各种可能结果发生的可能性不相等时,又该如何求事件发生的概率呢?共同探究自主学习教材,并回答下列问题:
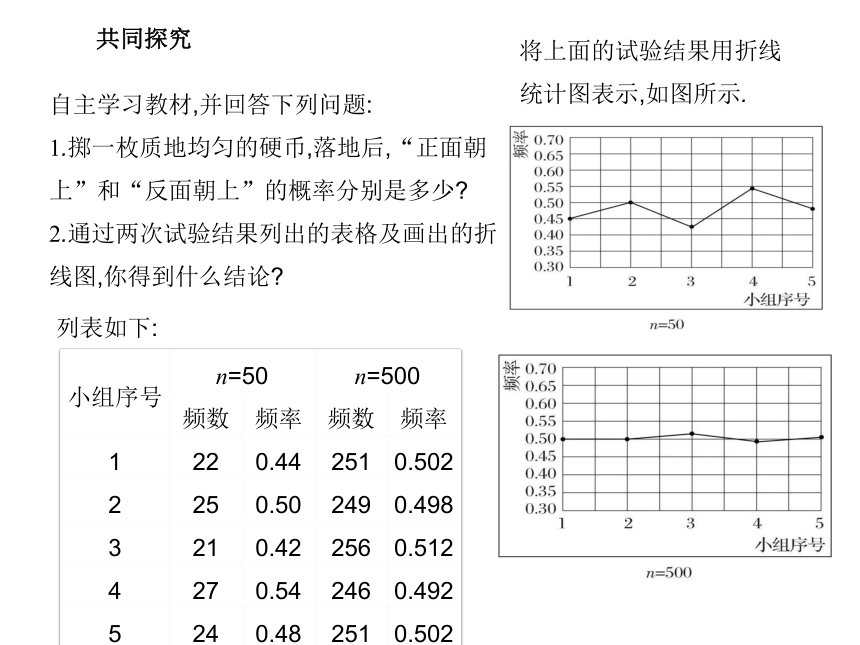
1.掷一枚质地均匀的硬币,落地后,“正面朝上”和“反面朝上”的概率分别是多少?
2.通过两次试验结果列出的表格及画出的折线图,你得到什么结论?列表如下:将上面的试验结果用折线统计图表示,如图所示.3.通过试验,可以看出同一事件频率和概率之间的关系吗?结论:
对掷硬币试验,“正面朝上”的概率为0.5,而频率则具有不确定性.试验次数不同,频率可能不同;即使是相同次数的不同试验,频率也可能不同.当试验次数较小时,频率的波动较大,但是随着试验次数的增大,“正面朝上”发生的频率波动明显减小,逐渐稳定到0.5附近.这个性质叫做频率的稳定性.做一做1.将全班分成12个小组,课外时间每个小组做20次掷硬币试验,记录事件A=“正面朝上”发生的次数.汇总各小组的试验结果,填写下表:2.整理上表中的数据,依次累计进行20次、40次、…、240次试验,记录事件A发生的次数,计算相应的频率,填写下表:3.在图中画折线统计图,表示事件“正面朝上”发生的频率的变化趋势.4.观察上面的统计表与统计图,随着投掷次数的增加,事件“正面朝上”发生的频率是如何变化的?是否逐渐稳定到0.5附近?1.某同学抛掷两枚硬币,分10组试验,每组20次,下面是共计200次试验中记录下的结果.根据下列表格内容填空:检测反馈(1)在他的10组试验中,抛出“两个正面”频数最少的是他的第 组试验.?
(2)在他的第1组试验中抛出“两个正面”的频数是 ,在他的前两组(第1组和第2组)试验中抛出“没有正面”的频数分别是 .?
(3)在他的10组试验中,抛出“两个正面”的频率是 ,抛出“一个正面”的频率是 ,“没有正面”的频率是 ,这三个频率之和是 .?解析:(1)观察试验结果可得抛出“两个正面”频数最少的是他的第9组试验;(2)第1组试验中抛出“两个正面”的频数是6,他的前两组试验中抛出“没有正面”的频数分别是3和8;(3)根据表中所显示的数据可知抛出“两个正面”的频率为: =0.265,抛出“一个正面”的频率是:
=0.52,抛出“没有正面”的频率是: =0.215,这三个频率之和是:0.265+0.52+0.215=1.963和8 0.2650.21512.小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,她们共做了60次试验,试验的结果如下:(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据上述试验,一次试验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗?为什么?解:(1)“3点朝上”的频率是 ;“5点朝上”的频率是 .(2)小颖的说法是错误的.因为“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的概率最大,只有当试验的次数足够大时,该事件发生的频率才稳定在事件发生的概率附近.
小红的说法也是错误的.因为事件的发生具有随机性,所以“6点朝上”的次数不一定是100次.
1.掷一枚质地均匀的硬币,落地后,“正面朝上”和“反面朝上”的概率分别是多少?
2.通过两次试验结果列出的表格及画出的折线图,你得到什么结论?列表如下:将上面的试验结果用折线统计图表示,如图所示.3.通过试验,可以看出同一事件频率和概率之间的关系吗?结论:
对掷硬币试验,“正面朝上”的概率为0.5,而频率则具有不确定性.试验次数不同,频率可能不同;即使是相同次数的不同试验,频率也可能不同.当试验次数较小时,频率的波动较大,但是随着试验次数的增大,“正面朝上”发生的频率波动明显减小,逐渐稳定到0.5附近.这个性质叫做频率的稳定性.做一做1.将全班分成12个小组,课外时间每个小组做20次掷硬币试验,记录事件A=“正面朝上”发生的次数.汇总各小组的试验结果,填写下表:2.整理上表中的数据,依次累计进行20次、40次、…、240次试验,记录事件A发生的次数,计算相应的频率,填写下表:3.在图中画折线统计图,表示事件“正面朝上”发生的频率的变化趋势.4.观察上面的统计表与统计图,随着投掷次数的增加,事件“正面朝上”发生的频率是如何变化的?是否逐渐稳定到0.5附近?1.某同学抛掷两枚硬币,分10组试验,每组20次,下面是共计200次试验中记录下的结果.根据下列表格内容填空:检测反馈(1)在他的10组试验中,抛出“两个正面”频数最少的是他的第 组试验.?
(2)在他的第1组试验中抛出“两个正面”的频数是 ,在他的前两组(第1组和第2组)试验中抛出“没有正面”的频数分别是 .?
(3)在他的10组试验中,抛出“两个正面”的频率是 ,抛出“一个正面”的频率是 ,“没有正面”的频率是 ,这三个频率之和是 .?解析:(1)观察试验结果可得抛出“两个正面”频数最少的是他的第9组试验;(2)第1组试验中抛出“两个正面”的频数是6,他的前两组试验中抛出“没有正面”的频数分别是3和8;(3)根据表中所显示的数据可知抛出“两个正面”的频率为: =0.265,抛出“一个正面”的频率是:
=0.52,抛出“没有正面”的频率是: =0.215,这三个频率之和是:0.265+0.52+0.215=1.963和8 0.2650.21512.小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,她们共做了60次试验,试验的结果如下:(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据上述试验,一次试验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗?为什么?解:(1)“3点朝上”的频率是 ;“5点朝上”的频率是 .(2)小颖的说法是错误的.因为“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的概率最大,只有当试验的次数足够大时,该事件发生的频率才稳定在事件发生的概率附近.
小红的说法也是错误的.因为事件的发生具有随机性,所以“6点朝上”的次数不一定是100次.
